[머신러닝] UCI Wholesale Dataset: KMeans 군집 분석
수행 내용
UCI Wholesale 데이터셋을 활용하여 데이터 분석 및 KMeans 군집화 수행
◆ UCI Wholesale 데이터셋이란?
https://archive.ics.uci.edu/dataset/292/wholesale+customers
UCI Wholesale 데이터셋은 도매 유통업체의 고객 구매 내역을 담고 있는 데이터셋으로, 각 고객의 연간 구매금액을 카테고리별로 구분하여 정리한 데이터셋이다.
사실, 해당 데이터셋을 수업 시간에 다뤄보기는 했는데, 이 데이터셋을 통해 알고자 하는 것이 무엇인지, 분석의 목적이 무엇인지, KMeans 같은 군집분석을 통해 알 수 있는 것에 대한 설명과 이해가 부족하여 혼자서 진행하며 제대로 이해해 보려고 한다.
◆ 이 데이터셋의 K-means 군집화 주요 목적
K-means 군집화는 데이터 분석에서 널리 사용되는 기법 중 하나로, 주어진 데이터셋을 유사한 특성을 가진 그룹으로 나누는 데 사용된다. UCI Wholesale 데이터셋은 도매 유통업체의 고객 구매 내역을 담고 있으며, 이를 활용한 K-means 군집 분석의 주요 목적은 다음과 같다.
1. 고객 세분화:
고객의 구매 패턴을 이해하고, 유사한 행동을 보이는 고객 그룹을 식별함으로써, 마케팅 전략을 세분화할 수 있다. 예를 들어, 특정 상품을 주로 구매하는 고객 그룹을 찾아 그 그룹에 맞는 맞춤형 광고 캠페인을 계획할 수 있다.
2. 재고 관리 및 최적화:
고객 군집의 구매패턴을 분석하여, 선호하는 제품군을 파악함으로써 적절한 재고량을 유지하고 효율적인 재고 관리를 도울 수 있다.
3. 고객 맞춤형 서비스 제공:
특정 군집 내 고객의 특성을 기반으로 개인화된 서비스를 제공하거나, 고객의 요구에 맞춘 새로운 상품 개발을 시도할 수 있다.
4. 비즈니스 전략 수립:
각 군집의 특성을 분석함으로써, 해당 군집에 적합한 비즈니스 전략을 설계하고, 수익성을 극대화할 수 있는 방향으로 나아갈 수 있다.
5. 이상치 탐지:
대다수의 고객과 다른 구매 행동을 보이는 이상 고객을 식별하여, 이들을 분석하고 필요한 경우 맞춤형 대응을 할 수 있다.
이러한 목적을 달성하기 위해, K-means 알고리즘을 적용하여 고객을 몇 개의 군집으로 나눈 후 각 군집의 특성을 분석하는 방식으로 진행할 수 있다.
K-Means와 군집화에 대해 더 궁금하다면,
[머신러닝] 군집화: k-평균
군집화란? [머신러닝] 군집화 (Clustering)군집화(Clustering) [군집]군집은 비슷한 샘플을 클러스터 또는 비슷한 샘플의 그룹으로 할당하는 작업으로, 데이터 분석, 고객 분류, 추천 시스템, 검색 엔
puppy-foot-it.tistory.com
해당 분석은 구글 코랩을 통해 진행되었다.
기본 설정
한글 설정 및 데이터 로드 위한 모듈 및 라이브러리 import
먼저, 코랩에서 맷플롯립 등의 시각화 사용 시 한글과 마이너스 기호의 출력이 문제 없도록 코드를 입력하고
# 한글 설정(코랩) - 폰트 설정
! sudo apt-get install -y fonts-nanum
!sudo fc-cache -fv
!rm ~/.cache/matplotlib-rfimport os
from matplotlib import font_manager
import matplotlib.font_manager as fm
import matplotlib.pyplot as plt
fe = fm.FontEntry(
fname=r'/user/share/fonts/truetype/nanum/NanumGothic.ttf', # ttf 파일이 저장되어 있는 경로
name='NanumGothic') # 원하는 폰트 설정
fm.fontManager.ttflist.insert(0, fe) # Matplotlib에 폰트 추가
plt.rcParams.update({'font.size': 18, 'font.family': 'NanumGothic'}) # 폰트 설정
plt.rcParams['axes.unicode_minus'] = False # 마이너스 값 출력
데이터 로드를 위해 필요한 판다스와 수를 다루기 위해 필요한 넘파이를 import 한다.
import pandas as pd
import numpy as np
그리고 데이터셋을 불러온다.
# 데이터셋 가져오기 (UCI ML Repository)
url_path = "https://archive.ics.uci.edu/ml/machine-learning-databases/00292/Wholesale%20customers%20data.csv"
data = pd.read_csv(url_path, header=0)
data.head()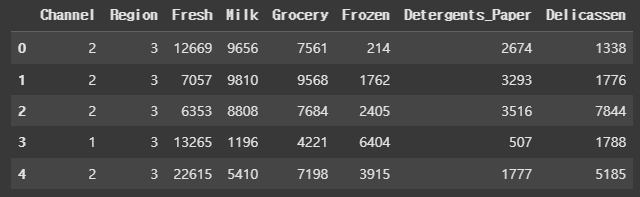
데이터셋 개요 및 탐색
각 피처와 해당 피처에 대한 대략적인 설명은 다음과 같다.
- FRESH: 신선 제품에 대한 연간 지출 (m.u.)
- MILK: 우유 제품에 대한 연간 지출 (m.u.)
- GROCERY: 식료품에 대한 연간 지출 (m.u.)
- FROZEN: 냉동 제품에 대한 연간 지출 (m.u.)
- DETERGENTS_PAPER: 세제 및 종이 제품에 대한 연간 지출 (m.u.)
- DELICATESSEN: 델리 및 특수 식품 제품에 대한 연간 지출 (m.u.)
- CHANNEL: 고객 채널 - 호텔(호텔/레스토랑/카페) 또는 소매 채널 (명목형)
- REGION: 고객 지역 - 리스본, 오포르토 또는 기타 (명목형)
데이터셋의 컬럼의 유형 및 인덱스 수를 알아본다.
data.info()
해당 데이터셋은 총 8개의 컬럼과 440개의 행(인덱스)으로 이루어져 있으며, 모두 정수형(int)의 데이터 타입이다.
모든 컬럼의 통계적인 정보도 알아본다.
data.describe()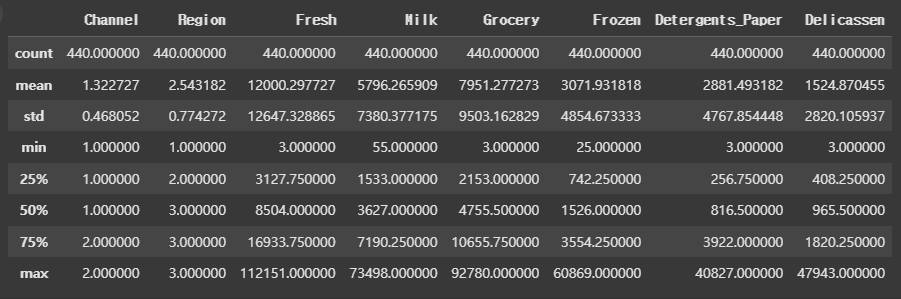
Channel(고객)과 Region(지역)의 경우, 앞서 말했듯이 명목형 데이터로 이루어져 있어 숫자가 수치로써의 역할을 하는 것이 아니라 수치적 분석이 의미가 없다.
또한, count의 경우 모두 해당 데이터셋의 인덱스 수인 440으로 되어 있는 것으로 보아, 결측치는 없는 것으로 추측된다. 과연 맞는지 확인해본다.
# 결측치 확인
data.isna().sum()
▶ 예상한대로 결측치는 없다.
그럼, 각 데이터의 상관 계수도 확인해 본다.
data.corr()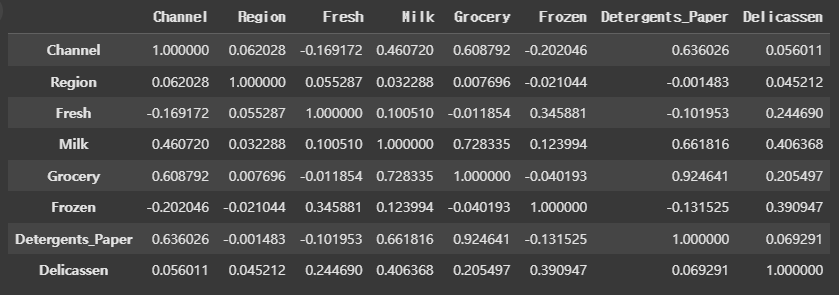
판다스의 scatter_matrix를 이용해 각 피처 간의 상관행렬도를 출력해 본다.
# 상관행렬도
from pandas.plotting import scatter_matrix
scatter_matrix(data, figsize=(12, 12));
◆ 명목형 데이터 확인
그럼 앞서 말한, 명목형 데이터인 Channel과 Region의 값은 어떻게 형성되어 있는지, 각 값의 데이터 수는 어떠한지 확인해본다.
# Channel과 Region 데이터 값 및 수 확인
columns = ['Channel', 'Region']
for i in data[columns]:
print(data[i].value_counts())
print('-' * 20)
▶ Channel 칼럼의 경우, 1과 2로 이루어져 있고 Region 칼럼의 경우 1,2,3의 값으로 이루어져 있다.
이 비중을 파이 차트로 시각화해본다.
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# 범주형 데이터로 구성된 칼럼
columns = ['Channel', 'Region']
fig, axes = plt.subplots(1, 2, figsize=(12,6))
for i, col in enumerate(columns):
data[col].value_counts().plot(kind='pie',
autopct='%2.f%%',
radius=2,
ax=axes[i],
colors=sns.color_palette('pastel'))
axes[i].set_title(col)
axes[i].set_ylabel("") # y축 레이블 제거
plt.tight_layout()
plt.show()
◆ 수치형 데이터 확인
이제 Channel과 Region을 제외한 나머지 수치형 데이터를 확인해본다.
그전에, 앞으로 'Channel'과 'Region' 피처는 분석에 필요 없으므로, 해당 피처를 삭제(drop)한 뒤 진행하도록 한다.
['CHANNEL'과 'REGION'이 군집 분석에 필요하지 않은 이유]
- 명목형 변수의 특성 정의: ' Channel '과 ' Region '은 명목형(nominal) 변수로, 구체적인 수치적 의미가 없고 단순히 카테고리를 나타낸다.
문제점: K-means와 같은 군집 분석 기법은 거리 기반 방법으로 수치형 데이터를 선호하는데, 명목형 데이터는 정량적 비교가 불가능하므로, 모델의 성능 저하를 초래할 수 있다.
- 정보의 중복 가능성 채널과 지역: ' Channel '이 호텔 또는 소매 채널을 나타내고, ' Region'이 지역(리스본, 오포르토 또는 기타)을 나타내므로, 이 두 변수는 서로 연관성이 강할 수 있다. 즉, 특정 지역에서 특정 채널이 선호될 수 있어, 군집 분석 결과에 중복된 정보만을 추가할 수 있다.
- 군집의 성격 왜곡 요소: 이러한 명목형 변수는 직접적인 구매 패턴과 관련이 없기 때문에, 군집 분석의 결과물을 왜곡할 수 있다. 예를 들어, 같은 채널이나 지역에 속하는 고객들의 구매 성향이 다를 수 있으므로, 군집을 잘못 형성할 가능성이 있다.
- 다양한 소비자 행동 분석의 필요 구매 성향 중심: 군집 분석의 목적은 고객의 구매 성향, 지출 패턴 등을 파악하는 것이므로, 연속형 수치 데이터(예: 신선 제품, 우유, 식료품 지출 등)에 초점을 맞추는 것이 더 효과적이다.
# 수치형 데이터 분석 및 시각화를 위한 범주형 피처 삭제
data.drop(['Region', 'Channel'], axis=1, inplace=True)
data.head(10)
히스토그램 시각화
# 수치형 데이터 히스토그램 시각화
data.hist(figsize=(20,10), bins=30, color='red', edgecolor='gold')
plt.show()
▶ 이 출력을 통해 변수의 분포가 매우 왜곡되어 있으며 이상치가 있을 수 있음을 추론할 수 있다.
[히스토그램에서 이상치가 있음을 확인하는 법]
히스토그램에서 나타나는 데이터의 분포를 살펴볼 때, 다음과 같은 점을 유의하면 좋다.
1. 드문 구간: 대부분의 데이터가 특정 구간에 집중되어 있고, 일부 구간에 데이터가 극히 적은 경우 해당 구간의 데이터는 이상치일 수 있다.
2. 긴 꼬리: 분포의 한쪽 끝에 긴 꼬리가 나타나는 경우, 이는 해당 방향으로 이상치가 존재할 가능성을 나타낸다.
혹시 모르니, pairplot 을 통해서도 시각화 해본다.
# 시본의 pairplot으로 각 피처 간 상관관계 시각화
sns.pairplot(data, kind='scatter', diag_kind='kde')
plt.show()
★ pairplot이란?
pairplot은 주로 seaborn 라이브러리에서 제공하는 시각화 도구로, 데이터프레임의 여러 변수들 간의 관계를 한꺼번에 시각화하는 데 유용하다. 이러한 관계를 이해함으로써 데이터의 분포, 상관관계, 패턴 및 이상치를 더 잘 파악할 수 있다.
[pairplot의 주요 기능]
- 변수 간 관계 시각화: 여러 변수 간의 산점도를 생성하여 두 변수 간의 관계를 한 눈에 확인할 수 있다.
- 대각선 플롯: 대각선에는 각 변수의 분포를 나타내는 히스토그램 또는 커널 밀도 추정(KDE) 그래프가 나타난다. 이는 변수 자체의 분포를 확인하는 데 유용하다.
- 구분된 색상: 범주형 변수를 색상으로 구분하여 특정 그룹 간의 차이를 시각적으로 쉽게 이해할 수 있다.
앞서 그렸던 pandas의 scatter_matrix와 비슷하지만, pandas의 scatter_matrix는 색상 및 마커 스타일에 대한 커스터마이징 옵션이 제한적이다. 기본적으로 모든 점은 같은 색상으로 표시되며, 색상 분류를 추가하려면 추가적인 전처리가 필요하다. 또한,사용이 간편하지만, 고급 시각화 기능은 제공되지 않는다.
어쨌든, 히스토그램, pairplot 두 시각화를 통해서 볼 수 있듯 각 피처에 이상치가 있는 것으로 보여 정확한 이상치를 탐지하고 제거하는 작업이 필요할 것으로 보인다.
이상치 탐지 및 처리
◆ 이상치 탐지 (IQR)
IQR 방식은 사분위(quantile)에 기초한 이상치 탐지 방식이다.
사분위는 전체 데이터를 25%(1사분위), 50%(2사분위, 중간값), 75%(3사분위), 100% 로 나눈다.
여기서 75% 지점의 값과 25% 지점의 값의 차이를 IQR이라고 한다.
IQR에 1.5를 곱해서 75% 지점의 값에 더하면 최댓값, 25% 지점의 값에서 빼면 최솟값으로 결정한다.
이 때, 결정된 최댓값보다 크거나 최솟값보다 작은 값을 이상치 라고 간주한다.
# IQR과 사분위수에 기초한 이상치 탐지 함수 설정
# IQR = q3-q1
def detect_outliers(data,column):
q1=data[column].quantile(0.25) # 1사분위
q3=data[column].quantile(0.75) # 3사분위
IQR=q3-q1
lower_bound=q1-IQR*1.5 # 최솟값 설정
upper_bound=q3+IQR*1.5 # 최댓값 설정
outliers=[] # 이상치를 담아둘 리스트 설정
for value in data[column]:
if( value> upper_bound) or (value<lower_bound):
outliers.append(value)
print(' column : ', column)
print('upper_bound is ',upper_bound,' lower_bound is ', lower_bound)
print('outliers : ',outliers)
print('이상치 개수:', len(outliers))
그리고, 이 함수를 반복문을 통해 실행하면
for i in data.columns:
detect_outliers(data,i)
print("-----------------")
각 칼럼명과 최댓값, 최솟값, 그리고 이상치 목록들과 이상치 갯수들이 출력된다.
◆ 이상치 처리
이상치를 처리하는 방식 역시 IQR 방식을 이용하는데, 앞서 구한 최솟값과 최댓값을 기준으로, 이상치가 최솟값보다 작으면 해당 값을 최솟값으로 바꾸고, 최댓값보다 크면 해당 값을 최댓값으로 변경하는 함수를 사용하여 처리한다.
# 이상치 처리 함수 정의 (IQR)
def handle_outliers(data,column):
q1=data[column].quantile(0.25)
q3=data[column].quantile(0.75)
IQR=q3-q1
lower_bound=q1-IQR*1.5
upper_bound=q3+IQR*1.5
for i in data.index:
value=data.loc[i,column]
if(value>upper_bound): # 값이 최댓값보다 클 경우
data.loc[i,column]=upper_bound # 최댓값으로 변경
elif(value<lower_bound): # 값이 최솟값보다 작을 경우
data.loc[i,column]=lower_bound # 최솟값으로 변경
print('이상치 처리 완료-->')
함수를 정의 후 반복문으로 실행하면
# 이상치 처리 함수 실행
for i in data.columns:
handle_outliers(data,i)
print("-----------------")
그리고나서 다시 pairplot 으로 시각화를 해본다.
sns.pairplot(data, kind='scatter', diag_kind='kde')
plt.show()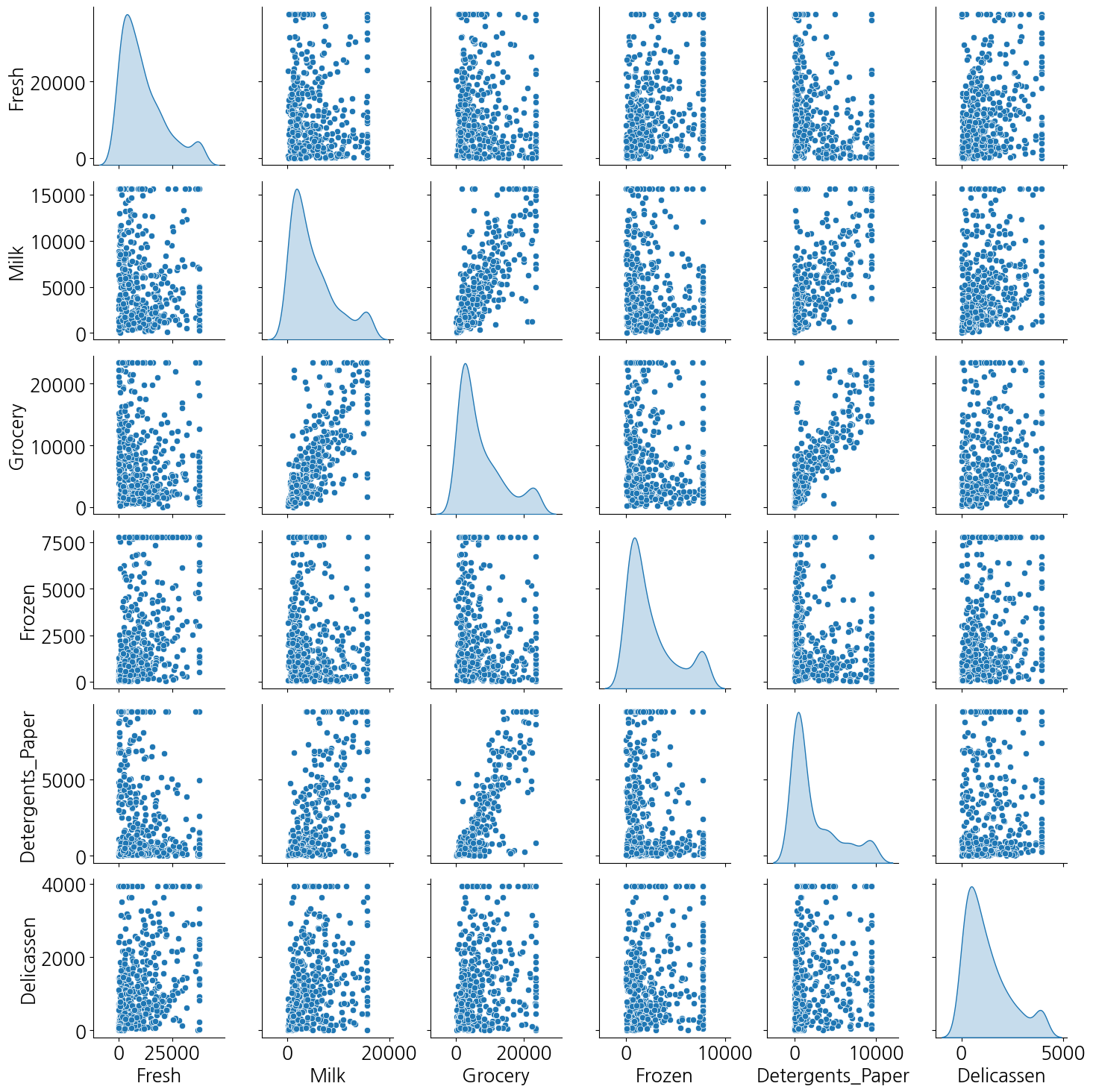
이상치 탐색 및 처리가 잘 완료되었다.
군집분석을 위한 최적의 클러스터 개수 확인
이제 해당 데이터셋으로 군집분석을 진행하려고 하는데, 군집분석에 사용할 모델은 KMeans(K-평균)이다.
◆ 이너셔를 통한 최적의 군집 수 파악
먼저, 최적의 군집(클러스터) 개수 k를 지정하는 것이 중요하므로, 먼저 k를 여러 개의 기준으로 지정한 뒤 이너셔를 출력하여 이를 선형그래프로 표현해 본다.
※ 이너셔는 클러스터 중심과 클러스터에 속한 샘플 사이의 거리의 제곱함을 말하며, 클러스터에 속한 샘플이 얼마나 가깝게 모여있는지를 나타내는 값으로, 클러스터 개수가 늘어날수록 클러스터 개개의 크기가 줄어들며 이너셔도 함께 감소하는 경향을 보인다.
from sklearn.cluster import KMeans
from sklearn.preprocessing import MinMaxScaler
# 피처 데이터 설정 (비지도 학습이므로, 타겟 데이터 없음)
X=data.iloc[::].values
print(X.shape)
# 데이터 스케일링
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)
# 최적의 클러스터를 찾기 위한 k평균 군집분석 실행
clusters = list(range(2, 6)) # 군집 수 2부터 5까지
inertias = []
for cluster in clusters:
model = KMeans(n_clusters=cluster, n_init=10, random_state=42)
model.fit(X)
inertias.append(model.inertia_)
# 이너셔 시각화
plt.plot(clusters, inertias)
plt.title("엘보우 포인트")
plt.xlabel("클러스터 수")
plt.ylabel("이너셔")
plt.show()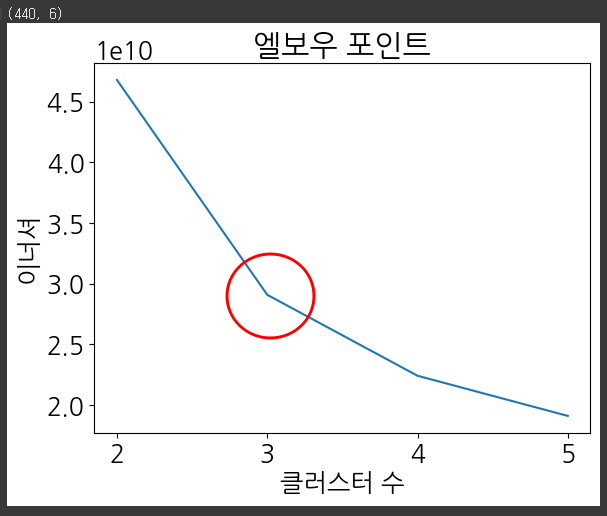
위의 시각화를 통해 이너셔는 k가 3까지 증가할 때 빠르게 줄어들며, k가 계속 증가하면 이너셔는 훨씬 느리게 감소한다. 따라서 이 그래프를 보면 k=3 지점이 엘보우며, k에 대한 정답을 모른다면 엘보우 포인트는 3이 좋은 선택이 된다.
※ 엘보우(Elbow)
성능 평가지표를 이용하여 최적의 군집수를 선택하는 방법 중 하나로 엘보우 포인트에서 최적 군집수를 결정하는 방식.
◆ 실루엣 계수 확인
from sklearn.metrics import silhouette_score
silhouette_score(X, model.labels_)
clusters = list(range(2, 6)) # 군집 수 2부터 5까지
silhouette_scores = []
for cluster in clusters:
model = KMeans(n_clusters=cluster, n_init=10, random_state=42)
model.fit(X)
silhouette_sc = silhouette_score(X, model.labels_)
silhouette_scores.append(silhouette_sc)
plt.figure(figsize=(8, 4))
plt.plot(clusters, silhouette_scores, "bo-")
plt.xlabel("$k$")
plt.ylabel("실루엣 점수")
plt.grid()
plt.show()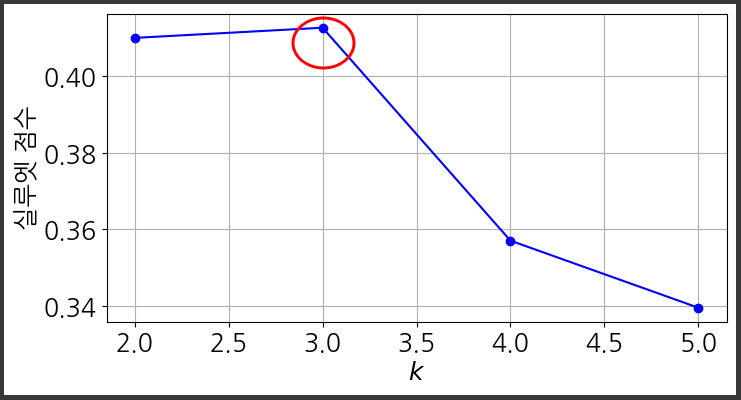
이너셔를 비교했을 때 보다 더 많은 정보를 준다.
- k=2 또는 k=3이 좋은 선택이며, k=4, k=4.5, k=5에 비해 좋은 선택이라는 것을 말해준다.
군집분석
KMeans
먼저, 앞서 나온 최적의 클러스터 수를 가지고 K-평균 군집 분석을 하고, 데이터를 모델에 학습하고 예측한다.
# 앞서 나온 최적의 클러스터 수를 가지고 k평균 군집 분석
kmeans = KMeans(n_clusters = 3, init='k-means++', random_state = 42)
# 학습 및 예측
y_kmeans = kmeans.fit_predict(X)
print(y_kmeans.shape)
print(y_kmeans)
예측된 값과 예측된 값의 군집 중심을 가지고 새로운 데이터프레임을 생성한 뒤 pairplot으로 시각화한다.
# 군집화된 데이터와 군집 중심(centroids)를 시각적으로 비교하기 위한 시각화 작업 수행
features = data.columns # 피처는 데이터프레임의 칼럼
df = pd.DataFrame(X, columns=features) # X와 피처로 이뤄진 새로운 데이터프레임 변수
df['Cluster'] = y_kmeans # 'Cluster' 칼럼을 만들고 예측값을 해당 칼럼에 저장
# 클러스터의 중심(센트로이드)와 피처로 이뤄진 데이터 프레임 생성
centroids_df = pd.DataFrame(kmeans.cluster_centers_, columns=features)
centroids_df['Cluster'] = ['Centroid'] * kmeans.n_clusters
# 원본 데이터(df)와 군집 중심 데이터(centroids_df)를 수직으로 결합
# 이때 ignore_index=True를 설정하여 인덱스를 새로 매김
# 전체 데이터와 군집 중심 모두를 포함
combined_df = pd.concat([df, centroids_df], ignore_index=True)
# 군집으로 구분된 pairplot 생성,
sns.pairplot(combined_df, hue='Cluster', palette='bright', markers=['o']*kmeans.n_clusters + ['X'])
plt.suptitle('센트로이도와 피처로 구성된 Pair Plot', y=1.02)
plt.show()
다음 내용
[참고]
UCI Machine Learning Repository
https://www.kaggle.com/code/enesfehmimanan/customer-segmentation-k-means-dbscan-gm
https://hwi-doc.tistory.com/
https://www.kaggle.com/code/zozays17/simplified-clustering-notebook-k-means-dbscan#-Wholesale-customers-
https://www.kaggle.com/code/kareemwael7007/simple-notebook-kmeans-dbscan-hierarchical#DBSCAN
https://www.kaggle.com/code/farhanmd29/unsupervised-learning
https://www.kaggle.com/code/adinishad/kmeans-clustering-from-scratch#dataset-describe