[빅분기 실기] 작업형 3유형 요약
이전 내용
[빅분기 실기] 작업형 3유형 : 로지스틱 회귀 분석
이전 내용 [빅분기 실기] 작업형 3유형 : 회귀 분석이전 내용 [빅분기 실기] 작업형 3유형 : 카이제곱 검정이전 내용 [빅분기 실기] 작업형 3유형 : 분산분석이전 내용 [빅분기 실기] 작업형 3유형 :
puppy-foot-it.tistory.com
작업형 3유형

작업형 3유형은 데이터 분석 과정에서 필요한 통계학적 접근 방법을 이해하고 적용할 수 있는 능력을 평가하기 때문에, 1과 2유형보다 이론적 내용을 더 많이 포함한 시험 문제를 출제한다.
3유형에서는 사이파이(scipy)와 스태츠모델즈(statsmodels) 같은 통계 분석을 위한 주요 파이썬 라이브러리를 활용해 수행한다.
- 가설검정: 주어진 데이터가 특정 가설을 지지하는지 여부를 통계적으로 검토하는 방법. 이를 통해 귀무가설과 대립가설을 설정하고 검정.
- 분산 분석: 두 개 이상의 집단 간의 평균 차이를 검정하기 위한 통계적 기법으로, 집단 간 분산과 집단 내 분산을 비교.
- 카이제곱 검정: 범주형 변수 간의 독립성을 검정하는 방법, 기대 빈도와 관측 빈도를 비교하여 결과 도출.
- 회귀 분석: 하나 이상의 독립 변수가 종속 변수에 미치는 영향을 모델링하는 기법, 선형 회귀가 가장 일반적.
- 로지스틱 회귀 분석: 이진 종속 변수를 예측하기 위해 사용되는 회귀 분석 기법, 사건의 확률을 추정하는 데 적합.
작업형 3유형 요약
1. 주요 개념
1-1. 표본 검정 종류와 설명
| 검정 이름 | 설명 | 예시 |
| 단일 표본 t-검정 | 모집단의 평균이 특정 값과 다른지 확인 (모집단 표준편차 모름) | 커피 평균 가격이 4,000원이 아닌지 확인 |
| 단일 표본 z-검정 | 모집단 평균 검정 (모집단 표준편차 알고 있을 때) | 전교생 수학 점수가 70점 이상인지 확인 |
| 두 표본 t-검정 | 두 그룹 평균 비교 | 남학생 vs 여학생 수학 점수 비교 |
| 대응 표본 t-검정 | 같은 대상의 전후 비교 | 다이어트 전후 체중 비교 |
| 독립 표본 t-검정 | 서로 다른 두 집단 비교 | A반과 B반 시험 점수 비교 |
| 카이제곱 검정 (χ²) | 범주형 데이터 비율 비교 | 남녀별로 선호하는 음료가 다른지 |
| 분산분석 (ANOVA) | 세 집단 이상의 평균 비교 | A/B/C 반의 시험 평균 차이 비교 |
1-2. 귀무가설, 대립가설
- 귀무가설: 기존에 알려진 사실
- 대립가설: 입증하고자 하는 가설
1-3. 가설 검정 단계
- 가설 설정 → 유의수준 설정 → 검정방법 설정 → p값 산출 → p값과 유의수준 비교 → 귀무가설 채택 / 대립가설 채택
| 조건 | 해석 |
| p-value < 0.05 | 귀무가설 기각 → 대립가설 채택 |
| p-value ≥ 0.05 | 귀무가설 기각 못 함 → 결론 내릴 수 없음, 귀무가설을 유지 |
2. 가설검정
2-1. 단일 표본 t-검정
scipy의 ttest_samp1() 함수 사용
from scipy import stats
stats.ttest_1samp(모집단 평균, 기준값)ex) 영화 평균 상영 시간이 120분이라는 가설을 설정했다고 한다면,
- 귀무가설: 평균 영화 상영 시간은 2시간이다.
- 대립가설: 평균 영화 상영 시간은 2시간이 아니다.
유의 수준이 0.05라고 한다면, 유의 확률(p-value)이 유의 수준보다 크다면 귀무가설을 채택하고, 유의 수준보다 작다면 귀무가설을 기각(대립가설 채택)
import pandas as pd
from scipy import stats
# 영화 러닝타임 데이터 (30편)
df = pd.DataFrame({
'running_time': [155, 122, 110, 119, 118, 117, 116, 105, 111, 119,
123, 105, 92, 110, 117, 145, 96, 121, 116, 123,
122, 117, 105, 107, 138, 142, 98, 100, 104, 105]
})
# 평균이 120분인지 검정 (단일 표본 t-test)
t_statistic, p_value = stats.ttest_1samp(df['running_time'], 120)
print(f"t-statistic: {t_statistic:.4f}, p-value: {p_value:.4f}")
print()
# 결과 해석
if p_value < 0.05:
print("p-value가 0.05보다 작으므로, 귀무가설을 기각합니다.")
print("→ 영화의 평균 상영 시간은 120분이 아니라고 할 수 있습니다.")
else:
print("p-value가 0.05보다 크므로, 귀무가설을 기각할 수 없습니다.")
print("→ 영화의 평균 상영 시간이 120분이라고 볼 수 있습니다.")
2-2. 양측 검정과 단측 검정
- 양측 검정: 모수에 대해 표본자료를 바탕으로 모수가 특정 값과 통계적으로 같은지 여부 판단 ▶ 영화의 평균 상영 시간이 120분인지 아닌 확인
- 단측 검정: 모수에 대한 표본자료를 바탕으로 모수가 특정 값과 통계적으로 큰지 작은지 여부 판단 ▶ 영화의 평균 상영 시간이 120분보다 짧은지 긴지 확인
scipy의 ttest_1sampe() 함수에서 alternative 파라미터 활용
| 대립가설 | alternative 값 | 비고 |
| 양측 검정 | two-sided | 기본값(생략 가능) |
| 단측 검정 | greater | 귀무가설의 평균보다 큼 |
| less | 귀무가설의 평균보다 작음 |
from scipy import stats
# 양측 검정
print("양측 검정 결과")
t_statics, p_value = stats.ttest_1samp(df['running_time'], 120, alternative='two-sided')
print(f"p-value: {p_value}")
# 단측 검정 (greater)
print("\n단측 검정 결과: 평균이 120분보다 큰지")
t_statics_1, p_value_1 = stats.ttest_1samp(df['running_time'], 120, alternative='greater')
print(f"p-value: {p_value_1}")
if p_value_1 < 0.05:
print("p-value가 유의수준보다 작으므로, 귀무가설을 기각한다.")
print("→ 영화의 평균 상영 시간은 120분보다 길다고 할 수 있다.")
else:
print("p-value가 유의수준보다 크므로, 귀무가설을 기각할 수 없다.")
print("→ 영화의 평균 상영 시간이 120분보다 길다고 보기 어렵다.")
# 단측 검정 (less)
print("\n단측 검정 결과: 평균이 120분보다 작은지")
t_statics_2, p_value_2 = stats.ttest_1samp(df['running_time'], 120, alternative='less')
print(f"p-value: {p_value_2}")
if p_value_2 < 0.05:
print("p-value가 유의수준보다 작으므로, 귀무가설을 기각한다.")
print("→ 영화의 평균 상영 시간은 120분보다 짧다고 할 수 있다.")
else:
print("p-value가 유의수준보다 크므로, 귀무가설을 기각할 수 없다.")
print("→ 영화의 평균 상영 시간이 120분보다 짧다고 보기 어렵다.")
2-3. 대응 표본 검정
scipy의 ttest_rel() 함수 활용
from scipy import stats
ttest_rel(a, b, alternative)| alternative 값 | 설명 |
| greater | a의 평균이 b의 평균보다 크다 |
| less | a의 평균이 b의 평균보다 작다 |
| two-sided | 양측 검정(기본값) |
★ ttest_rel(x, y, alternative='greater')는 내부적으로 t = mean(x - y)를 기준으로 비교하기 때문에, 어느 그룹이 앞에 오느냐에 따라 의미가 바뀌게 된다.
| 목적 | 함수 호출 형태 | alternative | 검정 내용 | 해석 |
| 다이어트 효과 있음 여부 | ttest_rel(after, before, alternative='greater') | 'greater' | after > before | → 체중 감소 |
| 다이어트 효과 없음 + 오히려 살쪘는지 | ttest_rel(before, after, alternative='less') | 'less' | before < after | → 체중 증가 |
from scipy import stats
before = [70, 72, 68, 75, 71] # 다이어트 약 복용 전 체중
after = [66, 70, 65, 72, 69] # 다이어트 약 복용 후 체중
# greater의 경우, after의 평균이 before의 평균보다 크다는 것을 검정하고자 할 때 사용
result = stats.ttest_rel(after, before, alternative='greater')
print("다이어트 약 복용 후 체중이 감소했는가? (약 효과 검정)")
print(f"t-statistic: {result.statistic:.4f}, p-value: {result.pvalue:.4f}")
if result.pvalue < 0.05:
print("p-value가 0.05보다 작음 → 귀무가설 기각")
print("→ 체중이 유의미하게 감소함 → 다이어트 약 효과 있음!")
else:
print("p-value가 0.05보다 큼 → 귀무가설 기각 불가")
print("→ 체중 감소는 통계적으로 유의하지 않음 → 다이어트 약 효과 없음")
print()
# less의 경우, before의 값이 after의 평균보다 작다는 것을 검정하고자 할 때 사용
result_2 = stats.ttest_rel(before, after, alternative='less')
print("다이어트 약 복용 후 체중이 오히려 증가했는가? (부작용 검정)")
print(f"t-statistic: {result.statistic:.4f}, p-value: {result.pvalue:.4f}")
if result.pvalue < 0.05:
print("p-value가 0.05보다 작음 → 귀무가설 기각")
print("→ 복용 후 체중이 유의미하게 증가함 → 다이어트 약이 효과 없고, 오히려 살이 찜")
else:
print("p-value가 0.05보다 큼 → 귀무가설 기각 불가")
print("→ 체중이 증가했다고 볼 수 없음 → 다이어트 약이 효과 없다고 볼 근거 없음")
2-4. 독립 표본 검정
| 검정 종류 | 설명 | 예시 |
| 대응 표본 t-검정(Paired t-test) | 같은 사람이나 같은 집단에서 두 시점의 측정값 차이를 비교할 때 사용 | 다이어트 약을 복용하기 전과 후의 몸무게를 같은 사람에게서 측정하여, 복용 효과를 비교 |
| 독립 표본 t-검정(Independent t-test) | 서로 다른 두 집단의 평균 차이를 비교할 때 사용 | 다이어트 약을 복용한 사람들과 복용하지 않은 사람들 두 집단 간의 체중 감소량 차이를 비교 |
독립 표본 검정에서 두 모평균을 비교할 때는 scipy.stats의 ttest_ind() 활용
ttest_ind(a, b, alternative, equal_var)| 파라미터 | 설명 |
| a | 첫 번째 모집단에서 뽑은 표본 데이터 |
| b | 두 번째 모집단에서 뽑은 표본 데이터 |
| alternative | greater, less, two-sided (기본값) |
| equal_var | 분산이 같은지 여부: True (같다고 가정) / False (다르다고 가정) |
어느 그룹의 몸무게를 통해 A그룹과 B그룹의 평균 몸무게 차이가 있는지 유의 수준 0.05 하에서 검정해 본다.
# 몸무게 평균 비교
import pandas as pd
from scipy.stats import ttest_ind
group_a = [85, 60, 72, 88, 66, 49, 53, 67]
group_b = [80, 72, 68, 55, 64]
print("양측 검정1: 모분산 동일")
print("귀무가설: 그룹별 몸무게 평균은 같다")
print("대립가설: 그룹별 몸무게 평균은 다르다")
t_statics1, p_value1 = ttest_ind(group_a, group_b)
if p_value1 < 0.05:
print(f"p_value가 {p_value1}로 유의수준보다 작으므로, 귀무가설 기각")
print("그룹 A와 그룹 B의 몸무게 평균은 다르다.")
else:
print(f"p_value가 {p_value1}로 유의수준보다 크므로, 귀무가설 기각 불가")
print("그룹 A와 그룹 B의 몸무게 평균은 같다고 볼 수 있다.")
print("\n양측 검정2: 모분산 다름")
t_statics2, p_value2 = ttest_ind(group_a, group_b, equal_var=False)
if p_value2 < 0.05:
print(f"p_value가 {p_value2}로 유의수준보다 작으므로, 귀무가설 기각")
print("그룹 A와 그룹 B의 몸무게 평균은 다르다.")
else:
print(f"p_value가 {p_value2}로 유의수준보다 크므로, 귀무가설 기각 불가")
print("그룹 A와 그룹 B의 몸무게 평균은 같다고 볼 수 있다.")
print("\n단측 검정1: 모분산 동일 - less")
print("귀무가설: 그룹별 몸무게 평균은 같다")
print("대립가설: 그룹B 평균 몸무게 > 그룹 A") # 앞이 적고, 뒤에가 많음
t_statics3, p_value3 = ttest_ind(group_a, group_b, alternative='less') # equal_var 생략 시 True
if p_value3 < 0.05:
print(f"p_value가 {p_value3}로 유의수준보다 작으므로, 귀무가설 기각")
print("그룹 B의 몸무게 평균이 더 많다.")
else:
print(f"p_value가 {p_value3}로 유의수준보다 크므로, 귀무가설 기각 불가")
print("그룹 B의 몸무게 평균이 더 많다고 볼 수 없다.")
print("\n단측 검정2: 모분산 동일 - greater")
print("귀무가설: 그룹별 몸무게 평균은 같다")
print("대립가설: 그룹A 평균 몸무게 > 그룹 B") # 앞이 많고, 뒤가 적음
t_statics4, p_value4 = ttest_ind(group_a, group_b, alternative='greater') # equal_var 생략 시 True
if p_value4 < 0.05:
print(f"p_value가 {p_value4}로 유의수준보다 작으므로, 귀무가설 기각")
print("그룹 A의 몸무게 평균이 더 많다.")
else:
print(f"p_value가 {p_value4}로 유의수준보다 크므로, 귀무가설 기각 불가")
print("그룹 A의 몸무게 평균이 더 많다고 볼 수 없다.")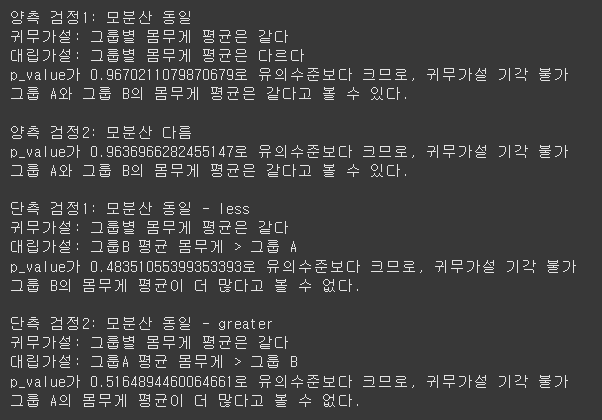
3. 분산 분석
3-1. 주요 개념
분산 분석: 여러 집단의 평균 차이를 통계적으로 유의미한지 검정하는 방법. ※ 주로 3개 이상의 집단 비교 시 사용
- 일원 분산 분석: 단일 요인의 수준 간 평균 차이 검정
- 이원 분산 분석: 두 요인의 수준 간 및 그들의 상호작용이 평균에 미치는 영향 검정
※ 요인: 독립변수로, 머신러닝에서는 '변수'를 의미.
◆ 분산 분석의 기본 가정
- 독립성: 각 집단의 관측치들은 모든 다른 집단의 관측치들과 독립적
- 정규성: 각 집단에서의 관측치는 정규 분포를 따름
- 등분산성: 모든 집단에서의 관측치는 동일한 분산을 가짐
◆ 일원 분산 분석의 귀무 가설과 대립 가설
- 귀무 가설: 모든 집단의 평균은 동일
- 대립 가설: 집단의 평균에는 차이가 있음. (적어도 두 그룹 간의 평균)
◆ 이원 분산 분석의 귀무 가설과 대립 가설
이원 분산 분석은 주 효과뿐 아니라 상호작용 효과에도 관심을 두기 때문에, 이원 분산 분석을 실시할 경우 주 효과 2개, 상호작용 효과 1개로 세 가지 가설을 세울 수 있다.
3-2. 일원 분산 분석 풀기
일원 분산 분석은 scipy의 f_oneway 사용
from scipy import stats
scipy.stats.f_oneway(sample1, sample2, sample3)
# sample은 각 집단 데이터- 정규성 검정 (shapiro): Shapiro-Wilk 검정은 각 그룹이 정규분포를 따르는지 확인하는 과정.
▶ p-value가 유의 수준보다 크면 정규 분포라고 판단하여 분산 분석 사용 가능 조건 충족
- 등분산성 검정(levene): Levene 검정은 세 그룹이 비슷한 분산을 갖는지 확인
▶ p-value가 유의 수준보다 크면 등분산 가정을 충족하여 모든 그룹의 분산이 동일하다고 판단 (일원 분산 분석 가능)
- 일원 분산 분석은 F-검정 통계량과 p-value를 반환
▶ p-value가 유의 수준보다 크면 평균이 동일하다고 볼 수 있어 귀무가설 채택 / 작으면 평균에 차이가 있다고 판단하여 귀무가설 기각
Q. 세 개 학급의 시험 점수 평균 비교
대학교 A학과에서는 세 개 반(1반, 2반, 3반)이 같은 시험을 봤다. 학생들이 얼마나 잘했는지 확인하고자, 각 반의 평균 점수가 통계적으로 차이가 있는지 알아보려 한다. (유의 수준 0.05)
- 귀무 가설: 세 반의 평균 시험 점수는 모두 같다
- 대립 가설: 적어도 하나의 반 평균은 다르다
# 일원 분산 분석
import pandas as pd
from scipy import stats
df = pd.DataFrame({
'class_1' : [82, 76, 91, 85, 77],
'class_2' : [89, 94, 90, 92, 88],
'class_3' : [70, 65, 72, 68, 74],
})
print("정규성 검정: p-value가 유의 수준보다 크면 정규 분포")
print(stats.shapiro(df['class_1']))
print(stats.shapiro(df['class_2']))
print(stats.shapiro(df['class_3']))
print("\n등분산성 검정: p-value가 유의 수준 보다 크면 모든 그룹의 분산 동일")
print(stats.levene(df['class_1'], df['class_2'], df['class_3']))
print("\n일원 분산 분석: p-value가 유의 수준 보다 크면 세 반의 평균 시험 점수는 모두 같다고 볼 수 있다 - 귀무 가설 채택")
print(stats.f_oneway(df['class_1'], df['class_2'], df['class_3']))
3-3. 이원 분산 분석 풀기
이원 분산 분석의 경우 스태츠모델즈(statsmodels)의 ols와 anova_lm 사용
import statsmodels.api as sm
from statsmodels.formula.api import ols
model = ols(종속변수 ~ 요인1 + 요인2 + 요인1:요인2).fit()
aonva_lm(model, typ=숫자)| 파라미터 | 설명 |
| 종속변수 | 연속형 변수 |
| 요인1 | 첫 번째 독립 변수(범주형 변수) |
| 요인2 | 두 번째 독립 변수(범주형 변수) |
| typ=1 | 변수의 순서에 따른 분석(기본값) |
| typ=2 | 각 변수의 독립적인 효과 분석 |
| typ=3 | 모든 변수와 상호작용을 동시에 고려해 분석 |
※ 만약, 범주형 변수가 1, 2, 3 과 같은 숫자로 되어있을 때는 연속형 변수로 잘못 해석될 위험이 있으므로 C()를 사용해 명확히 범주형으로 처리해줘야 한다.
[용어 해석]
| 용어 | 의미 | 설 |
| df (자유도) | 각 요인의 그룹 수 - 1 | 비교한 그룹의 수에 따라 달라짐 |
| Sum Sq (제곱합) | 전체 변동 중 이 요인이 설명하는 양 | 요인이 데이터의 차이에 얼마나 기여했는지 |
| Mean Sq (평균제곱) | 제곱합을 자유도로 나눈 값 | 비교 기준값 |
| F값 | 요인에 의한 분산 / 오차에 의한 분산 | F값이 클수록 요인의 효과가 크다는 뜻 |
| p-value | 귀무가설이 맞을 확률 | 0.05보다 작으면 의미 있는 차이 있음(귀무가설 기각) |
Q. 운동 종류와 성별에 따른 체중 감소 효과 분석
헬스장에서 다이어트 프로그램을 진행하며, 두 가지 요인(factor)을 비교하고자 한다.
- 요인1: 운동 종류 (달리기, 근력)
- 요인2: 성별 (남성, 여성)
import pandas as pd
from statsmodels.formula.api import ols
df = pd.DataFrame({
'gender': ['male']*6 + ['female']*6,
'type': ['run']*3 + ['weight']*3 + ['run']*3 + ['weight']*3,
'lose_weight': [3.2, 2.8, 3.0, 1.5, 1.8, 1.7, 2.5, 2.2, 2.3, 1.0, 0.9, 1.2]
})
model = ols('lose_weight ~ gender+type+gender:type', data=df).fit()
anova_table = sm.stats.anova_lm(model)
anova_table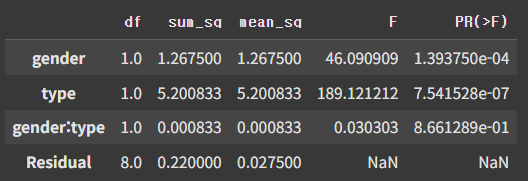
4. 카이제곱 검정
4-1. 카이제곱 검정 주요 개념
카이제곱 검정: 범주형 데이터의 관찰된 빈도와 기대된 빈도를 비교하여 두 변수 간의 독립성이나 분포의 적합성을 검정하는 방법
| 검정 분류 | 설명 | 귀무가설/대립가설 | 내용 | 사용 함수 (scipy) |
| 적합도 검정 | 1개의 범주형 변수가 특정 분포를 잘 따르고 있는지 검정하는 데 사용 | 귀무가설 | 특정 분포를 따른다 | chisquare(관측값, 예측값, 자유도, 축) |
| 대립가설 | 특정 분포를 따르지 않는다 | |||
| 독립성 검정 | 2개의 변수가 서로 독립적인지, 연관이 있는지 검정하는 데 사용 | 귀무가설 | 두 범주형 변수가 독립적(서로 연관성이 없음) | chi2_contingency(교차표, correction=True) |
| 대립가설 | 두 범주형 변수가 독립적이 아님(서로 연관성이 있음) | |||
| 동질성 검정 | 2개 이상의 집단에서 분산의 동질성을 가졌는지 검정하는 데 사용 | 귀무가설 | 모든 그룹의 분포나 비율이 동일 | chi2_contingency(교차표, correction=True) |
| 대립가설 | 모든 그룹의 분포나 비율이 동일하지 않음 |
4-2. 카이제곱 검정 풀기
1) 적합도 검정 (Chi-Square Goodness-of-Fit Test)
적합도 검정은 scipy의 chisquare 사용
from scipy import stats
scipy.stats.chisquare(observed, expected, ddof, axis)| 파라미터 | 설명 |
| observed | 관측값 |
| expected | 예측값 |
| dof | 자유도 |
| axis | 축(기본값 0) |
※ expected의 경우, 주어지지 않으면 모든 카테고리의 관측 빈도가 균일하고 관측 빈도의 평균으로 주어진다고 가정
Q. 주사위의 공정성 검정
한 대학생이 6면체 주사위가 공정한지 궁금해서, 주사위를 60번 던지고 나온 눈의 개수를 기록
| 주사위 눈 | 1 | 2 | 3 | 4 | 5 | 6 | 총합 |
| 관측도수 (Observed) | 5 | 8 | 9 | 10 | 13 | 15 | 60 |
유의수준(0.05)를 기준으로 이 주사위가 공정하다고 주장할 수 있는지를 검정
| 용어 | 설명 |
| 카이제곱 적합도 검정 | 관측된 데이터가 이론적인 기대 분포에 잘 맞는지 확인하는 검정 |
| 귀무가설 (H₀) | 주사위는 공정하다 (각 눈이 나올 확률은 1/6) |
| 대립가설 (H₁) | 주사위는 공정하지 않다 (적어도 하나의 눈 확률이 다르다) |
| 기대도수 (Expected) | 각 눈이 1/6 확률로 나온다면 기대되는 도수. 예: 60 × (1/6) = 10 |
# 주사위 적합도 검정
from scipy import stats
observed = [5, 8, 9, 10, 13, 15]
expected = [10, 10, 10, 10, 10, 10]
statistic, p_value = stats.chisquare(observed, expected)
print(f"검정 통계량: {statistic}, p-value: {p_value}")
if p_value < 0.05:
print("p-value가 유의수준보다 작으므로, 귀무가설 기각 -> 주사위는 공정하지 않다")
else:
print("p-value가 유의수준보다 크므로, 귀무가설 채택 -> 주사위는 공정하다")
2) 카이제곱 독립성 검정(Test of independence)
독립성 검정은 scipy의 chi2_contingency() 함수를 사용하여 카이제곱 통계량과 p-value를 구한다.
from scipy.stats import chi2_contingency
stats.chi2_contingency(table, correction=True)| 파라미터 | 설명 |
| table | 교차표 |
| correction | 연속성 보장 여부 (기본값 True) |
교차표 데이터가 제시된다면, 해당 내용을 교차표 데이터(데이터프레임)로 만들어야 한다.
※ 기대 빈도는 관찰된 데이터가 독립적일 경우 예상되는 빈도수를 나타낸다.
① 교차표 기반 카이제곱 검정
Q. 성별과 마라탕 선호도의 관계
한 마라탕 업체에서 성별과 마라탕 선호도의 관련이 있는지 설문조사를 했고, 그 결과는 아래와 같다.
| 성별 | 좋아함 | 좋아하지 않음 | 총합 |
| 남자 | 80 | 30 | 110 |
| 여자 | 90 | 10 | 100 |
| 총합 | 170 | 40 | 210 |
성별과 마라탕 선호도 사이에 통계적으로 유의한 관계가 있는지 유의 수준 0.05를 사용하여 검정
import pandas as pd
from scipy.stats import chi2_contingency
df = pd.DataFrame({
'좋아함': [80, 90],
'좋아하지 않음': [30, 10]},
index=['남자', '여자'])
# 카이제곱 검정 수행
statistic, p_value, ddof, expected = chi2_contingency(df, correction=True)
# 결과 출력
print(f"카이제곱 검정 통계량: {statistic:.4f}, p-value: {p_value:.4f}, 자유도: {ddof}, 기대 빈도: {expected}")
if p_value < 0.05:
print("p-value가 유의수준보다 작으므로, 귀무가설 기각 -> 성별과 마라탕은 독립적이지 않다.")
else:
print("p-value가 유의수준보다 크므로, 귀무가설 채택 -> 성별과 마라탕은 독립적이다.")
[기대 빈도]
- 89.0476: 남자가 좋아함을 선택할 것으로 기대되는 수
- 20.9523: 남자가 좋아하지 않음을 선택할 것으로 기대되는 수
- 80.9523: 여자가 좋아함을 선택할 것으로 기대되는 수
- 19.0476: 여자가 좋아하지 않음을 선택할 것으로 기대되는 수
[결과 해석]
| 항목 | 값 |
| 귀무가설 H₀ | 성별과 마라탕 선호는 독립이다 (서로 관련 없음) |
| 대립가설 H₁ | 성별과 마라탕 선호는 독립이 아니다 (관련 있음) |
| p-value | 약 0.0026 |
| 유의수준 α | 0.05 |
| 결론 | p-value < 0.05 → 귀무가설 기각 |
▶ 즉, 성별과 마라탕 선호 사이에는 통계적으로 유의한 관련이 있음
(남자와 여자가 마라탕을 좋아하는 비율이 유의하게 다름)
② 로우 데이터 기반 카이제곱 검정
문제에서 로우(원) 데이터 형태로 주어졌을 경우에는 로우 데이터를 pd.crosstab() 함수를 활용해 교차표로 변경한다.
교차표는 주로 변수 간의 관계를 비교할 때 사용한다.
import pandas as pd
df = pd.crosstab(df['요인1'],df['요인2'])앞서 마라탕과 성별의 선호도 관계에 대한 문제가 아래와 같이 주어졌다면,
| 성별 | 마라탕 |
| 남자 (110명) | 좋아함 (80명) |
| 좋아하지 않음(30명) | |
| 여자 (100명) | 좋아함 (90명) |
| 좋아하지 않음 (10명) |
import pandas as pd
data = {
'성별': ['남자']*110 + ['여자']*100,
'마라탕': ['좋아함']*80 + ['좋아하지 않음']*30 + ['좋아함']*90 + ['좋아하지 않음']*10
}
df = pd.DataFrame(data)
df = pd.crosstab(df['성별'], df['마라탕'])
df
3) 카이제곱 기반 동질성 검정 (Test of homogeneity)
카이제곱 기반 동질성 검정은 역시 독립성 검정과 동일하게 scipy의 chi2_contingency 를 사용
(계산하는 방식이 동일하나, 해석이 다름)
Q. 인문계와 이공계 학생의 선호과목 분포 동질성 검정
한 학교에서는 인문계와 이공계 학생들에게 어떤 과목을 가장 선호하는지 설문을 했다.
과목은 국어, 수학, 영어이며, 결과는 다음과 같다
| 계열 | 국어 | 수학 | 영어 | 합계 |
| 인문계 | 40 | 30 | 30 | 100 |
| 이공계 | 20 | 50 | 30 | 100 |
이 데이터를 바탕으로, 인문계와 이공계 학생들의 과목 선호 분포가 같은지 유의수준은 0.05를 사용하여 검정.
import pandas as pd
from scipy.stats import chi2_contingency
# 행방향 데이터
df = pd.DataFrame([[40, 30, 30], [20, 50, 30]],
columns=['국어', '수학', '영어'],
index=['인문계', '이공계'])
statistic, p_value, dof, expected = chi2_contingency(df)
# 결과 출력
print(f"검정 통계량: {statistic:.4f}, p-value: {p_value:.4f}, 자유도: {dof}, 기대빈도: {expected}")
# 결과 해석
if p_value < 0.05:
print("p-value가 유의수준보다 작으므로, 귀무가설 기각 -> 두 계열의 선호 과목은 동일하지 않다")
else:
print("p-value가 유의수준보다 므로, 귀무가설 채택 -> 두 계열의 선호 과목은 동일하다")
[결과 해석]
| 항목 | 값 | 해석 |
| 검정 통계량 | 11.6667 | 기대값과 관측값의 차이를 수치로 표현한 값 (차이가 클수록 값이 큼) |
| p-value | 0.0029 | 유의수준(0.05)보다 작으므로, 귀무가설을 기각해야 함 |
| 자유도 | 2 | (행 수 - 1) × (열 수 - 1) = (2-1) × (3-1) = 2 |
| 기대도수 | [[30. 40. 30.], [30. 40. 30.]] | 두 계열이 같은 분포를 보인다면 나올 것으로 기대되는 값들 |
▶ p-value가 0.0029로 0.05보다 작기 때문에, 귀무가설을 기각
따라서 인문계와 이공계는 과목 선호 분포가 다르다고 볼 수 있다.
5. 회귀 분석
5-1. 회귀 분석 주요 개념
회귀 분석: 수치형 변수 간의 관계 또는 원인과 결과 간의 관계를 추정하거나 예측하는 데 사용
상관 계수: 변수 간의 강도와 방향을 측정하는 방법으로, 변수 간의 관계를 파악
- 양의 상관 관계: 한 변수의 값이 증가할 때 다른 변수의 값도 증가 (상관 계수가 1에 가까움)
- 음의 상관 관계: 한 변수의 값이 증가할 때 다른 변수의 값은 반대로 감소 (상관 계수가 -1에 가까움)
- 상관 관계 없음: 한 변수의 값의 변화에 무관하게 다른 변수의 값이 변하는 상관 관계 (상관 계수가 0에 가까움)
※ 결정 계수(R-squared): 모델이 그 데이터를 얼마나 잘 설명하느냐를 나타내는 통계 값
▶ 1에 가까울수록 회귀 모델이 종속 변수의 변동을 더 잘 설명하는 것으로 해석. (모델의 설명력이 높음)
독립변수 개수에 따른 회귀 모델
- 독립변수 1개: 단순 선형 회귀
- 독립변수 2개 이상: 다중 선형 회귀
◆ 단순 선형 회귀선과 잔차
회귀선은 데이터를 설명하는 직선으로, 예측된 회귀선과 실제 data의 차이 (잔차, rasidual)가 0에 가까울수록 회귀선이 실제 값을 잘 설명한다고 할 수 있다.
- 최소제곱법(Ordinary Least Squares, OLS)
관측된 값과 회귀 모델의 예측값 간의 차이(잔차)의 제곱합을 최소화하는 것.
분석 시 statsmodels의 ols() 함수 활용.
- 제곱합(Sum of Ssquares)
모델이 데이터를 잘 설명하는가를 평가하는 데 사용하며, 총 제곱합(SST), 회귀 제곱합(SSR), 오차 제곱합(SSE)의 세 가지 제곱합이 있다. ▶ 최소 제곱법은 SSE를 최소화하는 회귀 계수를 찾는다.
◆ 다중 선형 회귀 분석
종속 변수를 가장 잘 설명하는 회귀 계수(기울기, 절편 등)를 추정.
단순 선형 회귀 분석에 비해 독립변수 개수만 다를 뿐, 분석 방법은 비슷.
◆ 범주형 변수
회귀 분석에서 범주형 변수는 회귀 모델에서 독립 변수로 사용하기 위해 통상적으로 인코딩을 해줘야 한다.
그러나, 숫자로 표현된 범주형 변수의 경우 회귀 모델에 직접 입력하면 모델이 이 변수를 연속형 수치 변수로 오해하고 분석할 수 있고, 그렇게 되면 변수의 실제 의미와 다르게 처리되어 분석결과에 오류를 초래할 수 있다.
따라서 숫자로 표현된 범주형 변수를 적절히 처리하는 것이 중요하다.
- 범주형 변수 자동 인식: statsmodels의 ols() 함수는 문자열로 된 범주형 변수를 자동 인식하여 원-핫 인코딩 수행.
- 수동 변환: 숫자로 된 범주형 변수를 statsmodels에서 범주형으로 처리하려면 범주형(C()) 으로 변환 필요
5-2. 회귀 분석 문제 풀기
| 주요 개념 | 사용 함수 | 파라미터 | 비고 |
| 상관 계수 | 판다스의 corr() | - method: 상관 관계 방법 - numeric_only: 숫자 자료형만 포함 |
method: - pearson (피어슨) - kendall (켄달 타우) - spearman (스피어만) |
| 단순 선형 회귀 분석 | statsmodels의 ols() | model = ols('종속변수 ~독립변수', data=df).fit() | model.summary()로 통계적 요약 출력 |
| 다중 선형 회귀 분석 | statsmodels의 ols() | model = ols('종속변수 ~독립변수1 + 독립변수2 + ... + 독립변수n', data=df).fit() | model.summary()로 통계적 요약 출력 |
| 범주형 변수 | statsmodels의 ols() | 범주형 변수 포함 시 자동으로 인식하여 자동 변환 | 숫자로된 변수의 경우, C(변수) |
1) 상관 계수
import pandas as pd
df = pd.DataFrame({..})
correlation = pd.corr(method='pearson', numeric_only=True)Q. 하루 평균 공부 시간과 시험 점수의 상관 계수
어떤 대학생 10명의 하루 평균 공부 시간과 시험 점수가 다음과 같다고 할 때, 이 두 변수 사이의 상관 계수를 계산하고, 관계를 해석하시오.
| 학생 번호 | 공부 시간(분) | 시험 점수 |
| 1 | 60 | 52 |
| 2 | 120 | 58 |
| 3 | 150 | 60 |
| 4 | 180 | 63 |
| 5 | 210 | 65 |
| 6 | 240 | 68 |
| 7 | 270 | 72 |
| 8 | 300 | 75 |
| 9 | 330 | 78 |
| 10 | 360 | 82 |
import pandas as pd
data = {
'공부시간': [60, 120, 150, 180, 210, 240, 270, 300, 330, 360],
'시험점수': [52, 58, 60, 63, 65, 68, 72, 75, 78, 82]
}
df = pd.DataFrame(data)
correlation = df.corr().iloc[0,1]
print(f"상관 계수: {correlation:.4f}")
if correlation > 0.5:
print("공부 시간과 시험 점수는 양의 상관 관계가 있다")
elif correlation < 0:
print("공부 시간과 시험 점수는 음의 상관 관계가 있다")
else:
print("공부 시간과 시험 점수는 상관 관계가 없다")
※ df.corr().iloc[0,1]을 사용하면 두 변수 중 하나의 상관 관계만 선택한다.
사용하지 않을 시, 아래와 같이 출력
correlation = df.corr()
print(f"상관 계수: {correlation}")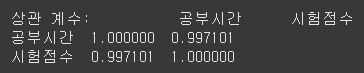
2) 단순 선형 회귀 분석
statsmodels.formula.api에서 ols() 함수를 불러온 뒤, 종속변수와 독립변수를 설정하고 선형 회귀 모델을 만든다.
Q. 공부 시간으로 시험 점수 예측하기
앞선 공부 시간(단위: 분)과 시험 점수 데이터를 바탕으로, 공부 시간이 늘어나면 시험 점수가 얼마나 오를지 단순 선형 회귀 모델 만들기
- 종속변수(Y): 예측하고 싶은 결과 ▶ 시험 점수
- 독립변수(X): 결과에 영향을 주는 요인 ▶ 공부 시간
1) 주어진 데이터로 최소제곱법을 이용한 단순 선형 회귀 모델을 구축하고 통계적 요약 출력
from statsmodels.formula.api import ols
# 공부시간: 독립변수, 시험점수: 종속변수
model = ols('시험점수 ~공부시간', data=df).fit()
print(model.summary())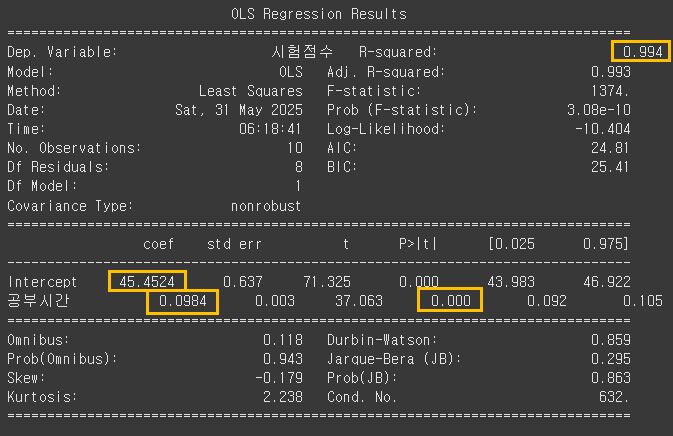
[모델 요약 결과]
- 공부 시간 기울기: coef 0.0984
- 절편(Intercept)의 기울기: coef 45.4524
- 결정 계수: R-sqaured 0.994
- 공부 시간의 p-value: 0.000
★ 각 모델에서 데이터를 가져오는 법
print("1. 회귀 모델의 결정계수")
print(model.rsquared)
print("\n2.회귀 계수(기울기와 절편)")
print(f"기울기: {model.params['공부시간']}, 절편: {model.params['Intercept']}")
print("\n3. 공부시간의 회귀 계수가 통계적으로 유의한지 검정 시 p-value")
print(f"p-value: {model.pvalues['공부시간']}")
print("\n4. 공부 시간이 195분일 때 예상 점수 출력")
new_data = pd.DataFrame({'공부시간': [195]})
result = model.predict(new_data)
print(f"공부 시간이 195분일 때 예상 점수: {result[0]}")
print("\n5. 회귀 모델의 잔차 제곱합")
df['잔차'] = df['시험점수'] - model.predict(df)
print(f"잔차 제곱합: {sum(df['잔차']**2)}")
print("\n6. 회귀 모델의 MSE")
MSE = (df['잔차']**2).mean()
print(f"MSE: {MSE}")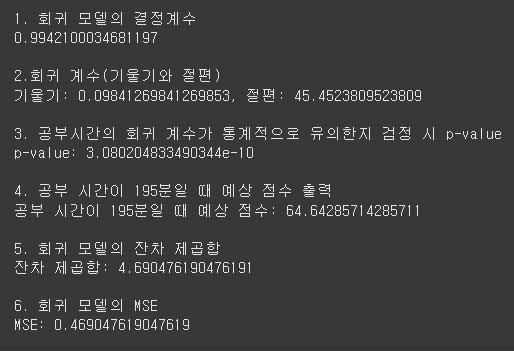
3) 다중 선형 회귀 분석
statsmodels.formula.api에서 ols() 함수를 불러온 뒤, 종속변수와 독립변수(2개 이상)를 설정하고 선형 회귀 모델을 만든다.
Q. 시험 점수 예측
한 고등학교에서 학생들의 시험 점수를 예측하기 위해 공부시간, 수면시간, 게임시간의 세 가지 요인을 분석하고자 한다
| 학생 | 공부시간(분) | 수면시간(분) | 게임시간(분) | 시험점수 |
| 1 | 60 | 300 | 300 | 52 |
| 2 | 120 | 360 | 180 | 58 |
| 3 | 150 | 300 | 240 | 60 |
| 4 | 180 | 420 | 120 | 63 |
| 5 | 210 | 360 | 60 | 65 |
| 6 | 240 | 300 | 120 | 68 |
| 7 | 270 | 360 | 60 | 72 |
| 8 | 300 | 360 | 60 | 75 |
| 9 | 330 | 420 | 0 | 78 |
| 10 | 360 | 480 | 0 | 82 |
다중 선형 회귀 모델을 구축하고 각 답을 구하라.
- 회귀식에서 유의한 독립변수는 무엇인가? (p-value < 0.05)
- 각 독립변수가 시험 점수에 미치는 영향은? (양의 상관관계, 음의 상관관계)
- 결정계수(R²)는 얼마인가? 이 모델은 시험 점수를 얼마나 잘 설명하는가?
- 공부시간 = 195분, 수면시간 = 300분, 게임시간 = 60분일 때, 예상 시험 점수는?
import pandas as pd
from statsmodels.formula.api import ols
data = {
'공부시간': [60, 120, 150, 180, 210, 240, 270, 300, 330, 360],
'수면시간': [300, 360, 300, 420, 360, 300, 360, 360, 420, 480],
'게임시간': [300, 180, 240, 120, 60, 120, 60, 60, 0, 0],
'시험점수': [52, 58, 60, 63, 65, 68, 72, 75, 78, 82]
}
df = pd.DataFrame(data)
# 독립변수: 공부시간, 수면시간, 게임시간
# 종속변수: 시험점수
model = ols('시험점수 ~ 공부시간+수면시간+게임시간', data=df).fit()
print(model.summary())
1) 회귀식에서 유의한 독립변수는 무엇인가? (p-value < 0.05)
print("1. 회귀식에서 유의한 독립변수는 무엇인가? (p-value < 0.05)")
columns = ['공부시간', '수면시간', '게임시간']
for column in columns:
p_value = model.pvalues[column] # p-value 값을 변수에 저장
print(f"p-value for {column}: {p_value:.4f}")
if p_value < 0.05:
print(f"{column}은 유의한 독립변수이다.\n")
else:
print(f"{column}은 유의한 독립변수가 아니다.\n")
2) 각 독립변수가 시험 점수에 미치는 영향은? (양의 상관관계, 음의 상관관계)
print("2. 각 독립변수가 시험 점수에 미치는 영향은? (음/양 상관관계)")
columns = ['공부시간', '수면시간', '게임시간']
for column in columns:
corre = df[column].corr(df['시험점수'])
print(f"{column}의 상관 계수: {corre}")
if corre > 0.5:
print(f"{column}은 시험점수와 양의 상관관계에 있다.\n")
elif corre < 0:
print(f"{column}은 시험점수와 음의 상관관계에 있다.\n")
else:
print(f"{column}은 시험점수와 상관관계가 없다.\n")
3)결정계수(R²)는 얼마인가? 이 모델은 시험 점수를 얼마나 잘 설명하는가?
print("3. 결정계수(R²)는 얼마인가? 이 모델은 시험 점수를 얼마나 잘 설명하는가?")
rsq = model.rsquared
print(f"결정계수: {rsq}")
if rsq > 0.5:
print("이 모델은 설명력이 높다고 볼 수 있다.")
else:
print("이 모델은 설명력이 낮다고 볼 수 있다")
4) 공부시간 = 195분, 수면시간 = 300분, 게임시간 = 60분일 때, 예상 시험 점수는?
print("4. 공부시간 = 195분, 수면시간 = 300분, 게임시간 = 60분일 때, 예상 시험 점수는?")
new_data = pd.DataFrame({'공부시간': [195], '수면시간': [300], '게임시간': [60]})
result = model.predict(new_data)
print(f"새로운 데이터의 예측 시험 점수: {result}")
5) 회귀 모델의 잔차의 제곱합 산출
df['잔차'] = df['시험점수'] - model.predict(df)
print(f"잔차 제곱합: {sum(df['잔차']**2)}") # 1.656971..
# 잔차: 실제값 - 예측값
# 잔차 제곱합: sum(잔차 **2)
6) 회귀 모델의 MSE 산출
MSE = (df['잔차'] ** 2).mean()
print(f"회귀 모델 MSE: {MSE}")MSE(Mean Squared Error, 평균 제곱 오차)
7) 각 변수별 95% 신뢰 구간 산출
conf_95 = model.conf_int(alpha=0.05)
print(f"95% 신뢰구간: {conf_95}")95% 신뢰 구간의 경우, model.summary() 함수에서도 확인할 수 있는데,
만약 95%가 아닌 다른 신뢰구간을 확인하고 싶은 경우에는
conf_int(alpha=) 로 확인할 수 있다. 만약 90%인 경우엔 alpha=0.1 로 하면 된다.
8) 공부시간: 172분, 수면 시간: 220분, 게임 시간: 50분일 때 신뢰 구간과 예측 구간 산출
new_data = pd.DataFrame({"공부시간": [172],
"수면시간": [220],
"게임시간": [50]})
pred = model.get_prediction(new_data)
result = pred.summary_frame(alpha=0.05)
print("예측값의 신뢰 구간과 예측 구간")
print(result)get_prediction() 함수와 summary_frame() 함수를 사용해 예측값과 신뢰 구간, 예측 구간을 구할 수 있다.
| 항목 | 설명 |
| mean | 예측값 평균 |
| mean_se | 예측값 확률분포의 표준편차 |
| mean_ci_lower / upper | 95% 신뢰 구간 하한값 / 상한값 |
| obs_ci_lower / upper | 예측 구간 하한값 / 상한값 |
※ 마찬가지로, alpha 에는 95% 신뢰구간일 경우 0.05를 입력한다.
4) 범주형 변수
statsmodels 의 ols() 함수는 회귀 모델 생성 시 범주형 변수가 포함돼 있을 경우 이를 자동으로 인식해 사용자가 별도로 범주형 변수를 수치형으로 변환하는 작업 없이 모델이 생성 가능하다.
- 종속 변수: lose_weight
- 독립 변수: ex_hours, ex_type
- ex_type의 경우 범주형 변수이나, 별도의 처리 없이 ols() 함수를 사용해 모델에 포함시킨다.
from statsmodels.formula.api import ols
model = ols('lose_weight ~ ex_hours + ex_type', data=df).fit()
print(model.summary())※ 만약, ex_type의 값들이 숫자로 되어 있었다면, 아래와 같이 사용한다.
model = ols('lose_weight ~ ex_hours + C(ex_type)', data=df).fit()6. 로지스틱 회귀 분석
6-1. 로지스틱 회귀 분석 주요 개념
로지스틱 회귀 분석: 선형 회귀 방식을 분류에 적용.
로지스틱 회귀 모델은 statsmodels 라이브러리를 사용하며, 모델 구축을 위해 logit() 함수를 사용한다. logit() 함수는 종속변수가 이진 형태(결과가 두 가지 범주 중 하나)인 경우, 독립변수들과의 관계를 모델링하는 데 사용된다.
from statsmodels.formula.api import logit
logit('종속변수~ 독립변수1 + 독립변수2 + ..'.data=df).fit()| 파라미터 | 설명 |
| 종속변수 | 예측하고 싶은 결과 - 이진형 변수. ex) 사건의 발생 여부 (발생 또는 미발생) |
| 독립변수 | 결과에 영향을 주는 요인으로, 종속변수를 예측하기 위해 포함 |
| data | 모델이 변수들을 찾아 사용할 데이터프레임 |
| .fit() | 로지스틱 회귀 모델이 주어진 데이터에 학습시키는 과정 수행 |
오즈와 오즈비
- 오즈: 어떤 사건이 발생할 확률과 그 사건이 발생하지 않을 확률의 비율
- 오즈비: 두 그룹의 오즈 간의 비율. 한 그룹에서 어떤 사건이 발생할 오즈가 다른 그룹에 비해 얼마나 더 큰지를 나타냄.
import numpy as np
np.exp(model.params['독립변수'])6-2. 로지스틱 회귀 분석 풀기
Q2. 운동 시간, 운동 종류, 식단 여부를 통해 다이어트 성공 여부 예측 (범주형 변수 포함)
100명의 데이터를 수집하여 다이어트 예측 모델 생성
import pandas as pd
from random import randint
import random
from statsmodels.formula.api import logit
members = 100
ex_types = ['러닝', '헬스', '요가']
df = pd.DataFrame({
'ex_hours': [randint(0, 10) for _ in range(members)],
'ex_type': [random.choice(ex_types) for _ in range(members)],
'diet': [randint(0, 1) for _ in range(members)]
})
model = logit('diet ~ ex_hours + C(ex_type)', data=df).fit()
print(model.summary())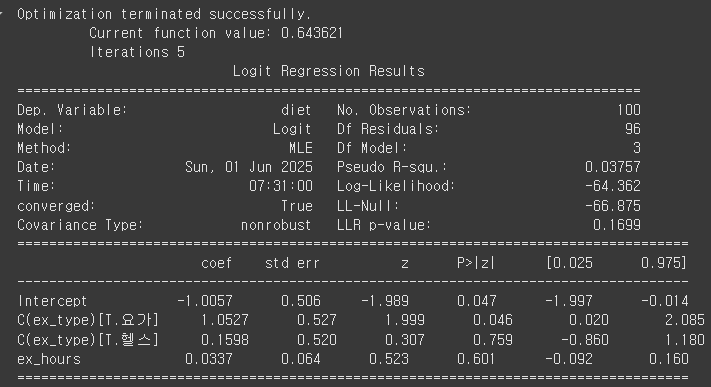
[결과 해석]
| 항목 | 값 | 해석 |
| Pseudo R-squared | 0.03757 | 모델 설명력: 약 3.7% |
| LLR p-value | 0.1699 | 모델이 유의미 하지 않음 (0.05보다 큼) |
| ex_hours P>|z| | 0.601 | 운동 시간 변수의 유의성 (0.05보다 큼) ▶ 유의하다고 보기 어려움 |
| Iterations | 5 | 최적화 알고리즘이 5번 반복되어 수렴함 |
| converged | True | 학습이 정상적으로 완료됨 |
[회귀 계수 해석]
| 변수 | 계수 (coef) | P-value | 해석 |
| Intercept (절편) | -1.0057 | 0.047 | 러닝 운동시간이 0일 때의 성공 확률(logit 기준) |
| C(ex_type)[T.요가] | 1.0527 | 0.046 | 요가는 다이어트 성공 확률 높음 |
| C(ex_type)[T.헬스] | 0.1598 | 0.759 | p값이 0.05보다 크므로, 헬스가 다이어트에 미치는 영향은 통계적으로 유의하지 않음. |
| ex_hours (운동 시간) | 0.0337 | 0.601 | 운동시간이 1시간 늘면, 성공 확률 증가 (그러나 통계적으로는 의미 없음) |
▶ ex_hours의 계수가 양수이므로, 운동 시간이 늘수록 성공 확률이 높아짐
- 오즈비 구하기
import numpy as np
ex_names = ['러닝', '헬스', '요가']
ex_types = ['Intercept', 'C(ex_type)[T.요가]', 'C(ex_type)[T.헬스]']
for ex_name, ex_type in zip(ex_names,ex_types):
print(f"{ex_name}: {np.exp(model.params[ex_type]):.4f}")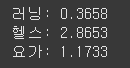
- 러닝: 0.3658
러닝을 하는 경우, 'diet'를 성공하는 오즈가 약 0.3658배라는 의미. 이는 러닝을 하는 경우 'diet'가 성공할 확률이 상대적으로 낮음을 나타낸다. 즉, 러닝을 하는 회원이 다이어트를 성공하는 확률이 적다는 것을 의미합니다.
- 헬스: 2.8653
헬스를 하는 경우, 'diet'를 성공하는 오즈가 약 2.8653배라는 의미. 이는 헬스를 하는 경우 'diet'가 성공할 확률이 약 2.87배 높다는 것을 의미한다. 따라서, 헬스는 다이어트 성공에 긍정적인 영향을 미치는 운동으로 해석할 수 있다.
- 요가: 1.1733
요가를 하는 경우, 'diet'를 성공하는 오즈가 약 1.1733배라는 의미. 이는 요가를 하는 경우 'diet'가 성공할 확률이 약 1.17배 높다는 것을 나타낸다. 그러나 이 값은 헬스와 비교했을 때 그리 높지 않으므로, 요가는 오히려 제한적인 영향을 미친다고 볼 수 있다.
▶ 종합 정리
- 러닝은 'diet'와 부정적인 연관성을 볼 수 있으며, 상대적으로 성공 확률이 적다.
- 헬스는 명백히 긍정적인 영향을 미치며, 다이어트를 성공하는 데 도움이 된다.
- 요가는 가벼운 긍정적 영향을 미치지만, 헬스만큼 두드러진 결과는 아니다.
- ex_hour가 3이고, ex_type이 요가일 때 다이어트 성공 확률은?
new_data = pd.DataFrame({'ex_hours': [3], 'ex_type': ['요가']})
result = model.predict(new_data)
print(f"운동시간이 3시간이고, 요가일 때 다이어트 성공 확률: {result}:.4f")
▶ 운동 시간이 3시간이고, 요가를 할 때 다이어트 성공 확률은 약 53.7% 이다.
다음 내용
[빅분기 실기] 실기 체험환경 (groom)
이전 내용 [빅분기 실기] 작업형 3유형 요약이전 내용 [빅분기 실기] 작업형 3유형 : 로지스틱 회귀 분석이전 내용 [빅분기 실기] 작업형 3유형 : 회귀 분석이전 내용 [빅분기 실기] 작업형 3유형 :
puppy-foot-it.tistory.com