이전 내용
[개발자를 위한 수학] 선형대수학: 행렬
이전 내용 [개발자를 위한 수학] 선형대수학: 벡터, 선형변환선형대수학 선형대수학(linear algebra): 벡터 공간, 벡터, 선형 변환, 행렬, 연립 선형 방정식 등을 연구하는 대수학의 한 분
puppy-foot-it.tistory.com
연립 방정식과 역행렬
선형대수학의 기본적인 사용 사례는 연립 방정식을 푸는 것이다.
다음과 같은 방정식이 주어졌을 때 x, y, z의 해를 구해야 한다고 가정해보자.
4x + 2y + 4z = 44
5x + 3y + 7z = 56
9x + 3y + 6z = 72
세 개의 변수를 분리하기 위해 다양한 대수 연산을 직접 실험해 볼 수도 있지만, 컴퓨터로 이 문제를 풀려면 다음과 같이 행렬로 표현해야 한다.
- 계수는 행렬 A로,
- 방정식의 오른쪽에 있는 값은 행렬 B로,
- 미지의 변수는 행렬 X로 추출한다.

선형 연립 방정식의 함수는 AX = B 이다. 행렬 X를 행렬 A로 변환해 행렬 B를 만들어야 한다.

A의 변환을 취소해야 X를 고립시키고, x,y,z 의 값을 구할 수 있다.
여기서 A의 변환을 취소하는 방법은 A의 역행렬을 구해서 행렬 곱셈으로 A에 적용하는 것인데,
이 역행렬을 계산하고 나서 A에 행렬 곱셈하면 대각선이 1이고 나머지는 모두 0인 항등 행렬이 만들어진다.
파이썬에서 항등 행렬을 만들려면 넘파이 대신 심파이를 사용하는 것이 좋다. 왜냐하면 넘파이의 부동 소수점은 행렬을 명확하게 표현하지 못하지만, 심파이를 사용해 기호 표현으로 수행하면 출력이 깔금하다.
심파이에서 행렬 곱셈을 수행하려면 @ 대신 * 를 사용해야 한다.
[심파이를 사용해 역행렬과 항등 행렬 만들기]
# 심파이를 사용해 역행렬과 항등 행렬 만들기
from sympy import *
# 4x + 2y + 4z = 44
# 5x + 3y + 7z = 56
# 9x + 3y + 6z = 72
A = Matrix([
[4, 2, 4],
[5, 3, 7],
[9, 3, 6]
])
# A와 그 역행렬의 점 곱은 항등 행렬을 만든다
inverse = A.inv() # 역행렬
identity = inverse * A # 역행렬 * A는 항등 행렬
print('역행렬: {}'.format(inverse))
print('항등 행렬: {}'.format(identity))

[넘파이를 사용해 연립 방정식 풀기]
# 넘파이를 사용해 연립 방정식 풀기
from numpy.linalg import inv
from numpy import array
# 4x + 2y + 4z = 44
# 5x + 3y + 7z = 56
# 9x + 3y + 6z = 72
A = array([
[4, 2, 4],
[5, 3, 7],
[9, 3, 6]
])
B = array([
44,
56,
72
])
X = inv(A).dot(B)
print(X)
[심파이를 사용해 연립 방정식 풀기]
# 심파이를 사용해 연립 방정식 풀기
from sympy import *
# 4x + 2y + 4z = 44
# 5x + 3y + 7z = 56
# 9x + 3y + 6z = 72
A = Matrix([
[4, 2, 4],
[5, 3, 7],
[9, 3, 6]
])
B = Matrix([
44,
56,
72
])
X = A.inv() * B
print(X)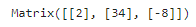
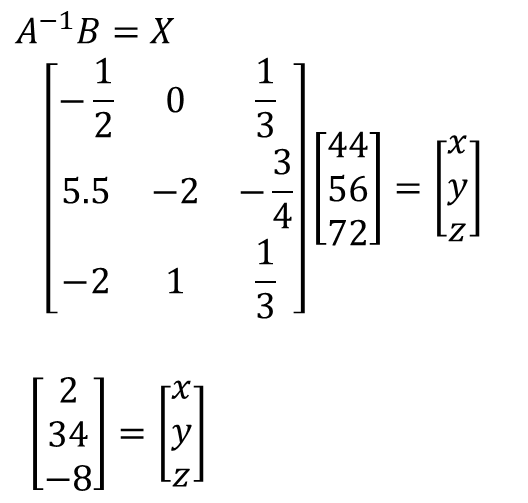
실제로 역행렬을 손으로 계산할 필요는 거의 없으며 컴퓨터가 대신 게산할 수 있다.
(만약 직접 계산해야 하거나, 계산법이 궁금하다면 '가우스 소거법' 에 대해 배우면 된다.)
★가우스 소거법
선형대수학에서 가우스 소거법(Gaussian elimination)이란, 연립일차방정식을 풀이하는 알고리즘이다. 풀이 과정에서, 일부 미지수가 차츰 소거되어 결국 남은 미지수에 대한 선형 결합으로 표현되면서 풀이가 완성된다. 가우스 소거법은 보통 행렬을 사용하며, 첨가 행렬을 그와 풀이가 같은 더 간단한 행렬로 변환하여 풀이를 완성한다. 가우스 소거법은 행렬식과 역행렬의 계산에도 응용된다.
다음 내용
[출처]
개발자를 위한 필수 수학
위키백과
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.4) -1 (0) | 2024.10.08 |
|---|---|
| [개발자를 위한 수학] 선형대수학: 고유 벡터와 고윳값 (2) | 2024.10.07 |
| [개발자를 위한 수학] 선형대수학: 행렬 (3) | 2024.10.07 |
| [개발자를 위한 수학] 선형대수학: 벡터, 선형변환 (1) | 2024.10.07 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.3)-2 (1) | 2024.10.07 |



