군집화란?
[머신러닝] 군집화 (Clustering)
군집화(Clustering) [군집]군집은 비슷한 샘플을 클러스터 또는 비슷한 샘플의 그룹으로 할당하는 작업으로, 데이터 분석, 고객 분류, 추천 시스템, 검색 엔진, 이미지 분할, 준지도 학습, 차원 축소
puppy-foot-it.tistory.com
이전 내용
[머신러닝] 군집화: GMM
군집화란? [머신러닝] 군집화 (Clustering)군집화(Clustering) [군집]군집은 비슷한 샘플을 클러스터 또는 비슷한 샘플의 그룹으로 할당하는 작업으로, 데이터 분석, 고객 분류, 추천 시스템, 검색 엔
puppy-foot-it.tistory.com
DBSCAN
◆ DBSCAN(Density Based Spatial Clustering of Applications with Noise)
밀도 기반 군집화의 대표적인 알고리즘이며, 밀집된 연속적 지역을 클러스터로 정의한다. 간단하고 직관적인 알고리즘으로 돼 있음에도 데이터의 분포가 기하학적으로 복잡한 데이터 세트에도 효과적인 군집화가 가능하다.
DBSCAN은 특정 공간 내에 데이터 밀도 차이를 기반 알고리즘으로 하고 있어서 복잡한 기하학적 분포도를 가진 데이터 세트에 대해서도 군집화를 잘 수행한다.
◆ DBSCAN의 장단점
[장점]
- 매우 간단하지만 강력하다
- 클러스터의 모양과 개수에 상관없이 감지할 수 있는 능력이 있다
- 이상치에 안정적이고 하이퍼파라미터가 두 개뿐이다
[단점]
- 클러스터 간의 밀집도가 크게 다르거나 일부 클러스터 주변에 저밀도 영역이 충분히 없는 경우 모든 클러스터를 올바르게 잡아내기 어려울 수 있다
- 대규모 데이터셋에 잘 확장되지 않을 수 있다.
◆ DBSCAN을 구성하는 중요한 두 가지 파라미터
- 입실론(epsilon) 주변 영역: 개별 데이터를 중심으로 입실론 반경을 가지는 원형의 영역
- 최소 데이터 개수(min points): 개별 데이터의 입실론 주변 영역에 포함되는 타 데이터의 개수
※ 입실론(Epsilon): 개별 데이터를 중심으로 일정한 반경을 가진 원형의 영역을 나타내는 값. (반경을 나타내는 값) .
◆ 입실론 주변 영역 내에 포함되는 최소 데이터 개수를 충족시키는지 여부에 따른 데이터 포인트 정의
- 핵심 포인트(Core Point): 주변 영역 내에 최소 데이터 개수 이상의 타 데이터를 가지고 있을 경우의 해당 데이터
- 이웃 포인트(Neighbor Point): 주변 영역 내에 위치한 타 데이터
- 경계 포인트(Border Point): 주변 영역 내에 최소 데이터 개수 이상의 이웃 포인트를 가지고 있지 않지만 핵심 포인트를 이웃 포린트로 가지고 있는 데이터
- 잡음 포인트(Noise Point): 최소 데이터 개수 이상의 이웃 포인트를 가지고 있지 않으며, 핵심 포인트도 이웃 포인트로 가지고 있지 않는 데이터
◆ DBSCAN에서 거리 측정 방식 선택
DBSCAN에서 어떤 거리 측정 방식을 사용할지는 데이터의 특성과 분석 목적에 따라 결정해야 함.
- 유클리드 거리: 데이터가 연속형이고 차원이 낮은 경우 적합
- 맨하탄 거리: 이상치가 많거나 데이터가 고차원인 경우 유용
- 마할라노비스 거리: 데이터의 상관관계를 고려해야 하는 경우 적합
◆ 작동 방식
- 알고리즘이 각 샘플에서 작은 거리인 e(입실론) 내에 샘플이 몇 개 놓여 있는지 세며, 이 지역을 샘플의 e-이웃 이라고 한다.
- 자기 자신을 포함해 e-이웃 내에 적어도 min_samples개 샘플이 있다면 이를 핵심 샘플로 간주한다. 즉, 핵심 샘플은 밀집된 지역에 있는 샘플을 의미한다.
- 핵심 샘플의 이웃에 있는 모든 샘플은 동일한 클러스터에 속한다. 이웃에는 다른 핵심 샘플이 포함될 수 있어 핵심 샘플의 이웃의 이웃은 계속해서 하나의 클러스터를 형성한다.
- 핵심 샘플이 아니고 이웃도 아닌 샘플은 이상치로 판단된다.
DBSCAN은 입실론 주변 영역의 최소 데이터 개수를 포함하는 밀도 기준을 충족시키는 데이터인 핵심 포인트를 연결하면서 군집화를 구성하는 방식이며, 모든 클러스터가 밀집되지 않은 지역과 잘 구분될 때 좋은 성능을 낸다.
DBSCAN vs K-Means
| 기준 | DBSCAN | K-Means |
| 클러스터 개수 | 자동 결정 | K값 사전 설정 필요 |
| 이상치 처리 | 이상치를 감지하고 제거 가능 | 이상치에 민감 |
| 클러스터 모양 | 비구형(비원형)도 가능 | 원형 클러스터에 적합 |
| 계산 속도 | 큰 데이터에서는 느릴 수 있음 | 비교적 빠름 |
| 밀도 차이 처리 | 밀도가 다른 클러스터 감지 가능 | 밀도가 다르면 군집 성능 저하 |
사이킷런에서의 DBSCAN
사이킷런은 DBSCAN 클래스를 통해 DBSCAN 알고리즘을 지원하며, 해당 클래스는 다음과 같은 주요한 초기화 파라미터를 가지고 있다.
- eps: 입실론 주변 영역의 반경
- min_samples: 핵심 포인트가 되기 위해 입실론 주변 영역 내에 포함돼야 할 데이터의 최소 개수 (자신의 데이터 포함)
DBSCAN 적용하기 - 초승달 데이터 세트
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=1000, noise=0.05)
dbscan = DBSCAN(eps=0.05, min_samples=5)
dbscan.fit(X)
모든 샘플의 레이블은 인스턴스 변수 lables_에 저장되어 있다.
dbscan.labels_
▶ 일부 샘플의 클러스터 인덱스는 -1인데, 이는 알고리즘이 이 샘플을 이상치로 판단했다는 의미이다.
핵심 샘플 확인하기
- 핵심 샘플의 인덱스: 인스턴스 변수 core_sample_indices_ 에서 확인
- 핵심 샘플 자체: 인스턴스 변수 components_에 저장
print('핵심 샘플 인덱스 수:', len(dbscan.core_sample_indices_))
print('핵심 샘플 인덱스:', dbscan.core_sample_indices_)
print('핵심 샘플:', dbscan.components_)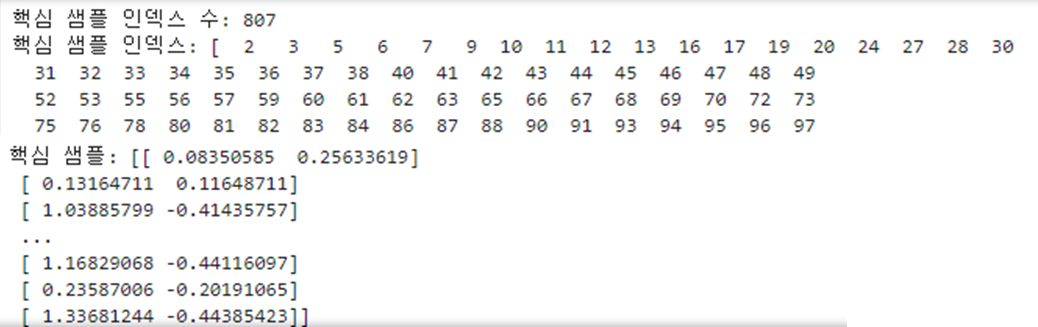
이 군집 결과를 그래프로 그리고, 그 옆에 eps를 0.2로 증가시킨 그래프도 같이 그려본다.
def plot_dbscan(dbscan, X, size, show_xlabels=True, show_ylabels=True):
core_mask = np.zeros_like(dbscan.labels_, dtype=bool)
core_mask[dbscan.core_sample_indices_] = True
anomalies_mask = dbscan.labels_ == -1
non_core_mask = ~(core_mask | anomalies_mask)
cores = dbscan.components_
anomalies = X[anomalies_mask]
non_cores = X[non_core_mask]
plt.scatter(cores[:, 0], cores[:, 1],
c=dbscan.labels_[core_mask], marker='o', s=size, cmap="Paired")
plt.scatter(cores[:, 0], cores[:, 1], marker='*', s=20,
c=dbscan.labels_[core_mask])
plt.scatter(anomalies[:, 0], anomalies[:, 1],
c="r", marker="x", s=100)
plt.scatter(non_cores[:, 0], non_cores[:, 1],
c=dbscan.labels_[non_core_mask], marker=".")
if show_xlabels:
plt.xlabel("$x_1$")
else:
plt.tick_params(labelbottom=False)
if show_ylabels:
plt.ylabel("$x_2$", rotation=0)
else:
plt.tick_params(labelleft=False)
plt.title(f"eps={dbscan.eps:.2f}, min_samples={dbscan.min_samples}")
plt.grid()
plt.gca().set_axisbelow(True)
dbscan2 = DBSCAN(eps=0.2)
dbscan2.fit(X)
plt.figure(figsize=(9, 3.2))
plt.subplot(121)
plot_dbscan(dbscan, X, size=100)
plt.subplot(122)
plot_dbscan(dbscan2, X, size=600, show_ylabels=False)
plt.show()
▶ 왼쪽은 클러스터를 7개(그래프 상 색상이 다른 개수) 만들고, 많은 샘플을 이상치(X 표시)로 판단했다.
오른쪽은 eps를 0.05에서 0.2로 증가시키며 이웃 범위를 넓혀 완벽한 군집을 얻었다.
DBSCAN 클래스는 predict() 메서드를 제공하지 않고 fit_predict() 메서드를 제공한다.
이는 이 알고리즘은 새로운 샘플에 대해 클러스터를 예측할 수 없다는 의미인데, 다른 분류 알고리즘이 새로운 데이터를 예측하는 것을 더 잘 수행할 수 있기 때문이다. 따라서 사용자가 필요한 예측기를 선택해야 한다.
예를 들어 KNeighborsClassifier를 예측기로 선택하고 훈련시킨다면
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=50)
knn.fit(dbscan.components_, dbscan.labels_[dbscan.core_sample_indices_])
그리고나서 샘플 몇 개를 전달하여 어떤 클러스터에 속할 가능성이 높은지 예측하고 각 클러스터에 대한 확률을 추정해 본다.
X_new = np.array([[-0.5, 0], [0, 0.5], [1,-0.1], [2, 1]])
knn.predict(X_new)
knn.predict_proba(X_new)
▶ 이 분류기를 핵심 샘플 뿐 아니라 모든 샘플에서 훈련할 수 있고, 이상치를 제외할 수 있다.
이 분류기의 결정 경계도 그려본다.
(덧셈 기호는 X_new에 있는 샘플 표시)
plt.figure(figsize=(6, 3))
plot_decision_boundaries(knn, X, show_centroids=False)
plt.scatter(X_new[:, 0], X_new[:, 1], c="b", marker="+", s=200, zorder=10)
plt.show()
훈련 세트에 이상이 없기 때문에 클러스터가 멀리 떨어져 있더라도 분류기는 항상 클러스터 한 개를 선택한다.
KNeighborsClassifier의 kneighbors() 메서드를 사용하면 최대 거리를 사용하여 두 클러스터에서 멀리 떨어진 샘플을 이상치로 간단히 분류할 수 있다. 이 메서드에 샘플을 전달하면 훈련 세트에서 가장 가까운 k개 이웃의 거리와 인덱스를 k개의 열을 가진 행렬 두 개를 반환한다.
y_dist, y_pred_idx = knn.kneighbors(X_new, n_neighbors=1)
y_pred = dbscan.labels_[dbscan.core_sample_indices_][y_pred_idx]
y_pred[y_dist > 0.2] = -1
y_pred.ravel()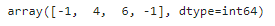
DBSCAN 적용하기 - 붓꽃 데이터 세트
붓꽃 데이터 세트를 DataFrame으로 로딩하고, DBSCAN 클래스를 이용해 붓꽃 데이터 세트를 군집화
(일반적으로 eps 값으로 1 이하의 값을 설정한다)
from sklearn.datasets import load_iris
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
iris = load_iris()
feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
# 데이터 핸들링을 위해 DataFrame 변환
irisDF = pd.DataFrame(data=iris.data, columns=feature_names)
irisDF['target'] = iris.target
dbscan = DBSCAN(eps=0.6, min_samples=8, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)
▶ 군집 레이블이 -1인 것은 노이즈에 속하는 군집을 의미한다.
Target 값의 유형이 3가지인데, 군집이 2개가 됐다고 군집화 효율이 떨어지는 것은 아니다.
DBSCAN은 군집의 개수를 알고리즘에 따라 자동으로 지정하므로 DBSCAN에서 군집의 개수를 지정하는 것은 무의미하다.
[PCA를 이용해 2개의 피처로 압축 변환한 뒤, 시각화]
DBSCAN으로 군집화 데이터 세트를 2차원 평면에서 표현하기 위해 PCA를 이용해 2개의 피처로 압축 변환한 뒤, 이전에 진행했던 visualize_cluster_plot() 함수를 이용해 시각화해 본다.
visualize_cluster_plot() 함수 인자로 사용하기 위해 irisDF의 'ftr1', 'frt2' 칼럼에 PCA 로 변한된 피처 데이터 세트를 입력한다.
def visualize_cluster_plot(clusterobj, dataframe, label_name, iscenter=True):
# 군집별 중심 위치: K-Means, Mean Shift 등
if iscenter:
centers = clusterobj.cluster_centers_
# Cluster 값 종류
unique_labels = np.unique(dataframe[label_name].values)
markers=['o', 's', '^', 'x', '*']
isNoise=False
for label in unique_labels:
# 군집별 데이터 프레임
label_cluster = dataframe[dataframe[label_name]==label]
if label == -1:
cluster_legend = 'Noise'
isNoise=True
else:
cluster_legend = 'Cluster '+str(label)
# 각 군집 시각화
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], s=70,
edgecolor='k', marker=markers[label], label=cluster_legend)
# 군집별 중심 위치 시각화
if iscenter:
center_x_y = centers[label]
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=250, color='white',
alpha=0.9, edgecolor='k', marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k',
edgecolor='k', marker='$%d$' % label)
if isNoise:
legend_loc='upper center'
else:
legend_loc='upper right'
plt.legend(loc=legend_loc)
plt.show()
from sklearn.decomposition import PCA
# 2차원으로 시각화하기 위해 PCA n_components=2 로 피처 데이터 세트 변환
pca = PCA(n_components=2, random_state=0)
pca_transformed = pca.fit_transform(iris.data)
# visualize_cluster_plot() 함수는 ftr1, ftr2 칼럼을 좌표에 표현하므로 PCA 변환값을 해당 칼럼으로 생성
irisDF['ftr1'] = pca_transformed[:, 0]
irisDF['ftr2'] = pca_transformed[:, 1]
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)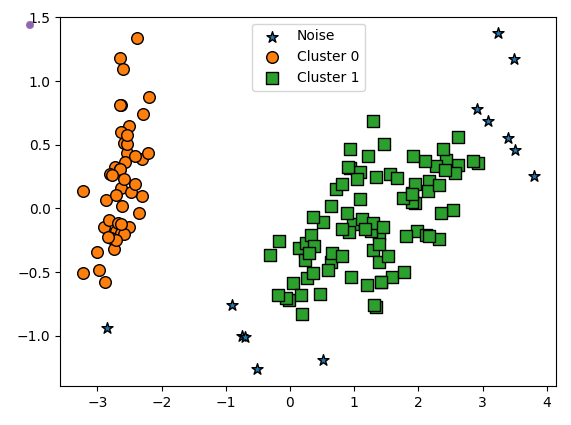
▶ '★' 로 표현된 값은 모두 노이즈이며, PCA로 2차원으로 표현하면 이상치인 노이즈 데이터가 명확히 드러난다.
DBSCAN을 적용할 때는 특정 군집 개수로 군집을 강제하지 않는 것이 좋으며, DBSCAN 알고리즘에 적절한 eps와 min_samples 파라미터를 통해 최적의 군집을 찾는 게 중요하다.
- eps의 값을 크게 하면 반경이 커져 포함하는 데이터가 많아지므로 노이즈 데이터 개수가 작아진다
- min_samples 를 크게 하면 주어진 반경 내에서 더 많은 데이터를 포함시켜야 하므로 노이즈 데이터 개수가 커지게 된다 (데이터 밀도가 더 커저야 하는데, 매우 촘촘한 데이터 분포가 아닌 경우 노이즈로 인식하기 때문)
[eps를 증가시켰을 경우 노이즈 데이터 변화 확인]
eps를 0.6에서 0.8로 증가시킨 후 시각화를 해 본다.
dbscan = DBSCAN(eps=0.8, min_samples=8, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)
▶ 노이즈 군집인 -1이 3개로 줄었다.
[min_samples를 증가시켰을 때의 변화 확인]
이번에는 eps 를 0.6으로 유지하고 min_samples를 16으로 늘려본 후 데이터 변화를 확인해 본다.
dbscan = DBSCAN(eps=0.6, min_samples=16, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)
▶ 노이즈 데이터가 기존보다 많이 증가하였다.
DBSCAN 적용하기 - make_circles() 데이터 세트
[복잡한 기하학적 분포를 가지는 데이터 세트에서 DBSCAN과 타 알고리즘 비교]
make_circles() 함수를 이용해 내부 원과 외부 원 혀태로 돼 있는 2차원 데이터 세트를 만든다.
make_circles() 함수는
- 오직 2개의 피처만을 생성하므로 별도의 피처 개수를 지정할 필요가 없음.
- 파라미터 noise: 노이즈 데이터 세트의 비율
- 파라미터 factor: 외부 원과 내부 원의 scale 비율
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, shuffle=True, noise=0.05, random_state=0, factor=0.5)
clusterDF = pd.DataFrame(data=X, columns=['ftr1', 'ftr2'])
clusterDF['target'] = y
visualize_cluster_plot(None, clusterDF, 'target', iscenter=False)
[K-평균의 데이터 세트 군집화 확인]
# KMeans로 make_circles() 데이터 세트 군집화 수행
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, max_iter=1000, random_state=0)
kmeans_labels = kmeans.fit_predict(X)
clusterDF['kmeans_cluster'] = kmeans_labels
visualize_cluster_plot(kmeans, clusterDF, 'kmeans_cluster', iscenter=True)
▶ 거리 기반 군집화로는 위와 같이 데이터가 특정한 형태로 지속해서 이어지는 부분을 찾아내기 어렵다.
[GMM 의 데이터 세트 군집화 확인]
# GMM으로 make_circles() 데이터 세트 군집화 수행
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=2, random_state=0)
gmm_labels = gmm.fit(X).predict(X)
clusterDF['gmm_cluster'] = gmm_labels
visualize_cluster_plot(gmm, clusterDF, 'gmm_cluster', iscenter=False)
▶ 내부와 외부의 원형으로 구성된 복잡한 형태의 데이터 세트에서는 군집화가 원하는 방향으로 되지 않는다.
[DBSCAN 군집화]
# DBSCAN 으로 make_circles() 데이터 세트 군집화 수행
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.2, min_samples=10, metric='euclidean')
dbscan_labels = dbscan.fit_predict(X)
clusterDF['dbscan_cluster'] = dbscan_labels
visualize_cluster_plot(dbscan, clusterDF, 'dbscan_cluster', iscenter=False)
▶ 원하는 방향으로 정확히 군집화가 되었다.
다음 내용
[머신러닝] 군집화: 실습 - 고객 세그먼테이션
군집화란? [머신러닝] 군집화 (Clustering)군집화(Clustering) [군집]군집은 비슷한 샘플을 클러스터 또는 비슷한 샘플의 그룹으로 할당하는 작업으로, 데이터 분석, 고객 분류, 추천 시스템, 검색 엔
puppy-foot-it.tistory.com
[출처]
파이썬 머신러닝 완벽 가이드
핸즈 온 머신러닝
'[파이썬 Projects] > <파이썬 머신러닝>' 카테고리의 다른 글
| [머신러닝] 텍스트 분석 (0) | 2024.10.28 |
|---|---|
| [머신러닝] 군집화: 실습 - 고객 세그먼테이션 (1) | 2024.10.28 |
| [머신러닝] 군집화: GMM (0) | 2024.10.27 |
| [머신러닝] 군집화: 평균 이동 (0) | 2024.10.25 |
| [머신러닝] 군집화: 군집 평가 (3) | 2024.10.25 |



