[목차]
[빅데이터 분석기사] 시험 과목 및 주요 내용 (필기)
빅데이터 분석기사 (필기) 시험 과목 및 주요 내용 출처: 데이터자격검정 (dataq.or.kr) 필기과목명 주요항목 세부항목 세세항목 빅데이터 분석 기획 빅데이터의 이해 빅데이터 개요 및 활용 빅데이
puppy-foot-it.tistory.com
빅데이터 탐색 - 통계기법의 이해
<기술 통계>
1. 데이터 요약 - 대푯값 / 산포도 / 데이터 분포 / 공분산 / 상관관계 / 상관 계수
- 데이터 분석의 목적으로 수집된 데이터를 확률-통계적으로 정리-요약하는 기초적인 통계
- 분석의 초기 단계에서 데이터 분포의 특징을 파악하려는 목적으로 산출
(1) 대푯값: 주어진 자료 전체에서 중심 위치를 나타내는 값
평균, 중위수, 최빈수, 사분위수, 백분위수
ㄱ. 평균 (Mean) : 일반적으로 산술 평균
- 산술 평균: 자료를 모두 더한 후 자료 개수로 나눈 값 (전부 같은 가중치를 두며 이상값에 민감, 모평균, 표본평균)
- 기하 평균: 숫자들을 모두 곱한 후 거듭제곱근을 취해서 얻는 평균 (자료가 비율이나 배수와 같이 곱의 관계일 때 사용)
- 조화 평균: 자료들의 역수에 대해 산술 평균을 구한 후 그것을 역수로 취한 평균 (속도의 평균, 여러 곳의 평균 성장률 등에 사용)
ㄴ. 중위수 (Median)
- 모든 데이터 값을 오름차순으로 순서대로 배열하였을 때 중앙에 위치한 데이터 값 (이상치에 영향 받지 않음)
- 데이터값의 수가 홀수: 중위수는 하나
- 데이터값의 수가 짝수: 중앙에 있는 두 개의 값을 평균으로 하여 정함
ㄷ. 최빈수 (Mode)
- 데이터 값 중에서 빈도수가 가장 높은 데이터 값
- 관측된 데이터 값 중에서 가장 여러 번 나타난 값
ㄹ. 사분위수
- 모든 데이터값을 순서대로 배열하였을 때 4등분한 지점에 있는 값
- 제1 사분위수: 데이터를 오름차순 했을 때 첫 번째 사등분점
- 제2 사분위수(중위수): 두 번째 사등분점
- 제3 사분위수: 세 번째 사등분점
ㅁ. 백분위수
- 모든 데이터값을 순서대로 배열하였을 때 100등분한 지점에 있는 값
| 백분위수 | 사분위수 |
| 25백분위수 | 제1 사분위수 |
| 50백분위수 (중앙값) | 제2 사분위수 (중위수) |
| 75백분위수 | 제3 사분위수 |
(2) 산포도: 주어진 자료가 흩어진 정도를 나타내는 값
분산, 표준편차, 범위, IQR, 사분편차, 변동계수
ㄱ. 분산
- 평균으로부터 얼마나 떨어져 있는지를 나타내는 값
- 양의 편차와 음의 편차를 더할 경우 0이 될 수 있으므로 각 데이터값을 제곱 후 모두 더함
- 모분산, 표본분산 등
ㄴ. 표준편차; 분산에 양의 제곱근을 취한 값 (모 표준편차, 표본 표준편차)
ㄷ. 범위: 자료 중에서 최댓값과 최솟값의 차이
ㄹ. IQR (사분 범위, 사분위수 범위): 제3 사분위수와 제1 사분위수의 차이 값
ㅁ. 사분편차: 제3 사분위수와 제1 사분위수 차이인 IQR의 절반 값
ㅂ. 변동계수
- 표춘편차를 평균으로 나눈 값
- 측정 단위가 서로 다른 자료의 흩어진 정도를 상대적으로 비교할 때 사용
(3) 데이터 분포
첨도, 왜도
ㄱ.첨도: 데이터 분포의 '뾰족한 정도'를 설명하는 통계랑
ㄴ. 왜도: 데이터 분포의 기울어진 정도를 설명하는 통계량 (비대칭성 표현)
(4) 공분산
- 2개의 변수 사이의 관련성을 나타내는 통계량
- 모공분산: 모집단 X, 모집단 Y 변수 사이의 상관 정도를 나타내는 값
- 표본공분산: 표본 집단 X, 표본 집단 Y 변수 사이의 상관 정도를 나타내는 값
- 상관 관계의 상승 혹은 하강하는 경향을 이해할 수 있음
- 공분산 값의 크기는 측정 단위에 따라 달라지므로 선형관계의 강도를 나타내지는 못함
(5) 상관관계
- 두 변수 사이에 어떤 선형적 또는 비선형적 관계가 있는지를 분석 (인과관계는 알 수 없음)
- 분류 개수에 따른 분류: 분석의 대상이 되는 변수의 개수가 두 개 > 단순 상관 분석 / 3개 이상 > 다중 상관 분석
- 변수 속성에 따른 분류:
| 속성 | 설명 | 분석 방법 |
| 수치적 데이터 | -등간 척도, 비율 척도 - 수치로 표현을 할 수 있는 측정 가능한 데이터 변수 - 변수의 연산 가능 |
피어슨 상관계수 |
| 순서적 데이터 | - 범주형 데이터 중 순서적 데이터 - 데이터의 순서에 의미를 부여 - 변수의 연산 불가 |
스피어만 순위 상관 계수 |
| 명목적 데이터 | - 범주형 데이터 중에서 명목척도 - 데이터의 특성을 구분하기 위하여 숫자나 기호를 할당한 데이터 변수 - 변수의 연산 불가 |
카이제곱 검정 |
(6) 상관 계수
- 두 변수 사이의 연관성을 수치상으로 객관화하여 두 변수 사이의 방향성과 강도 표현
- 모상관계수: 모집단을 대상으로 계산된 상관계수
- 표본상관계수: 표본집단을 대상으로 계산된 상관계수
- 두 변수 간에 직선 관계가 있는지를 나타내는 통계량 (통계적 유의성을 알 수 없음)
- 상관계수 행렬: 두 변수 간의 선형 상관관계를 계량화한 행렬
- 두 변수가 같이 커지거나 같이 작아지는 경향이 있으면 상관 계수가 높음
- 상관 계수가 높은 변수가 여럿 존재하면 파라미터 수가 불필요하게 증가 → 차원 저주에 빠질 우려
- 선형 모델, 신경망 등의 기계 학습 모델은 상관 계수가 큰 예측 변수들이 있을 경우 성능이 떨어지거나 모델이 불안정해질 수 있으므로 상관 계수가 큰 변수들을 제거 가능
| 구분 | 종류 | 설명 |
| 수치적 데이터 | 모집단 피어슨 상관계수 |
모집단 X, 모집단 Y 변수 사이의 상관 정도를 나타내는 값 |
| 표본집단 피어슨 상관계수 |
표본 집단 X, 표본 집단 Y 변수 사이의 상관 정도를 나타내는 값 | |
| 순서적 데이터 | 모집단 스피어만 상관계수 |
모집단 X의 순위를 나타낸 변수를 R, 모집단 Y의 순위를 나타낸 변수를 S라고 할 때, 순위 변수 R, S 사이의 상관 정도를 나타내는 값 |
| 표본집단 스피어만 상관계수 |
표본 집단 X의 순위를 나타낸 변수를 R, 표본 집단 Y의 순위를 나타낸 변수를 S라고 할 때, 순위 변수 R, S 사이의 상관 정도를 나타내는 값 | |
| 명목적 데이터 | 카이제곱 검정 (교차 분석) |
명목적 데이터일 경우 (지역, 종교 등) 두 변수 사이의 연관성 분석 |
★ 차원의 저주란?
차원의 저주는 데이터의 차원이 증가함에 따라 데이터 분석의 효율성과 정확도가 급격히 감소하는 현상을 말한다. 이 현상은 고차원의 데이터 공간에서 데이터 포인트들이 희박하게 분포하게 되어, 데이터 간의 거리가 멀어지는 현상 때문에 발생한다.
[머신러닝] 차원의 저주(Curse of Dimensionality)란?
고차원의 데이터 분석에서 발생하는 문제를 설명하는 용어로 "차원의 저주(Curse of Dimensionality)"가 있습니다. 이 문제는 특히 빅데이터 분석과 머신러닝에서 많이 다뤄지며, 데이터
puppy-foot-it.tistory.com
2. 표본 추출
(1) 표본 추출 (표본 표집, 표본 선정)
- 모집단 일부를 일정한 방법에 따라 표본으로 선택하는 과정
(2) 종류 - 단순 무작위 추출 / 계통 추출 / 층화 추출 / 군집 추출
- 단순무작위 추출: 모집단에서 정해진 규칙 없이 표본 추출 (표본의 크기가 커질수록 정확도가 높아지며, 추정값이 모수에 근접하므로 추정값의 분산 감소)
- 계통 추출: 모집단을 일정한 간격으로 추출하는 방식
- 층화 추출: 모집단을 여러 계층으로 나누고, 계층별로 무작위 추출을 수행 (층내는 동질적, 층간은 이질적)
- 군집 추출: 모집단을 여러 군집으로 나누고, 일부 군집의 전체를 추출하는 방식 (집단 내부는 이질적, 집단 외부는 동질적)
3. 확률분포
(1) 확률 - 베이즈 정리 / 베이지안 네트워크
- 비슷한 현상이 반복해서 일어날 경우에 어떤 사건이 발생할 가능성을 0과 1 사이의 숫자로 표현하는 방법
- 교사건: 사건 A와 B에 동시에 속하는 기본 결과들의 모임
- 조건부 확률: 어떤 사건이 일어난다는 조건에서 다른 사건이 일어날 확률 (두 개의 사건 A와 B에 대하여 사건 A가 일어난다는 선행조건 아래에 사건 B가 일어날 확률)
- 전 확률의 정리: 나중에 주어지는 사건 A의 확률을 구할 때 그 사건의 원인을 여러 가지로 나누어서, 각 원인에 대한 조건부 확률 P와 그 원인이 되는 확률 P의 곱에 의한 가중합으로 구할 수 있다는 법칙
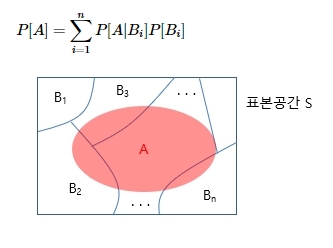
- 베이즈 정리: 어떤 사건에 대해 관측 전(사전확률) 원인에 대한 가능성과 관측 후 (사후확률)의 원인 가능성 사이의 관계를 설명하는 확률이론
[확률과 통계] 14. 베이즈 정리, Bayes' Theorem / Bayes' Rule
'베이즈 통계학'은 기존 통계학과 큰 차이점이 있습니다. 기존 통계학에서는 모집단을 변하지 않는 대상으...
blog.naver.com
- 베이지안 네트워크: 랜덤 변수의 집합과 방향성 비순환 그래프를 통하여 그 집합을 조건부 독립으로 표현하는 확률의 그래프 모형
【 도대체 베이지안 네트워크가 뭐야? ①】
* 베이지안 네트워크(BN; Bayesian Network) 란? 확률 변수(RV; Random variables)들 사이의 조건부 독립 등의 관계를 보임으로써, RV의 full joint distribution등을 간결하게 표현할 수 있는 그래프 표기법 (Graphical
jaysung00.github.io
(2) 확률분포 및 확률변수 - 확률변수(기댓값/분산) / 채비셰프 정리
- 확률분포는 확률변수가 특정한 값을 가질 확률을 나타내는 분포
- 확률분포는 확률변수의 종류에 따라 이산확률분포와 연속확률분포로 나뉨.
- 확률변수는 특정 확률로 발생하는 결과를 수치적 값으로 표현하는 변수
- 확률변수는 확률에 의해 그 값이 결정되는 변수
- 확률변수는 주로 대문자 X로 표시
[확률변수 - 기댓값]
- 기댓값은 확률변수의 값에 해당하는 확률을 곱하여 모두 더한 값
- 확률변수의 평균과 같으며, E(X)로 표시
- 해당 확률분포에서 평균적으로 기대할 수 있는 값이며, 해당 확률분포의 중심 위치를 설명해주는 값
[수리통계학] 확률변수의 기댓값(Expectation of Random Variable)
HTML 삽입 미리보기할 수 없는 소스 Review 참고 포스팅 : 2023.09.14 - [Statistics/Mathematical Statistics] - [수리통계학] 확률변수(Random Variable ; R.V.) [수리통계학] 확률변수(Random Variable ; R.V.) Review # 해당 포스
datalabbit.tistory.com
[확률변수 - 분산]
- 확률변수의 산포도를 나타내는 값으로 V(X) 또는 Var(X)로 표시
[확률과 통계] 3.통계 - 확률변수의 평균, 분산, 표준편차
안녕하세요. 포항에서 제일 똘똘한 지효석 선생님입니다. 오늘은 확률 변수의 평균, 분산, 표준편차...
blog.naver.com
[체비셰프 정리]
- 임의의 양수 k에 대하여 확률변수가 평균으로부터 k배의 표준 편차 범위 내에 있을 확률에 대한 예측값을 보수적으로 제공하는 정리
- 관측값들의 분포에 상관없이 성립하지만, 확률에 대한 하한값만을 제공
[기초통계학] 체비셰프 부등식(Chebyshev Inequality)
Review 참고 포스팅 : 2020/05/26 - [Statistics/Basic Statistics] - [기초통계학] 마르코프 부등식(Markov Inequality) [기초통계학] 마르코프 부등식(Markov Inequality) Review 참고 포스팅 : 2020/05/18 - [Statistics/Basic Statisti
datalabbit.tistory.com
(3) 확률분포 종류 - 포아송분포, 베르누이분포, 이항분포, 초기하분포, 연속확률분포,
ㄱ. 이산확률분포
- 이산확률변수 X가 가지는 확률분포
- 확률변수 X가 0, 1, 2, 3, ..과 같이 하나씩 셀 수 있는 값을 취함
- 포아송분포: 이산형 확률분포 중 주어진 시간 또는 영역에서 어떤 사건의 발생 횟수를 나타내는 확률 분포
- 베르누이분포: 특정 실험의 결과가 성공 또는 실패로 두 가지의 결과 중 하나를 얻는 확률분포
- 이항분포: n번 시행 중에 각 시행의 확률이 p일 때, k번 성공할 확률분포
- 초기하분포: 비복원추출에서 N개 중에 r개가 특정 그룹이고, n번 추출했을 때 특정 그룹에서 x개가 뽑힐 확률의 분포
[확률 질량 함수(PMF; Probability Mass Function)]
- 이산확률변수에서 특정 값에 대한 확률을 나타내는 함수
[누적 질량 함수(CMF; Cumulative Mass Function)]
- 이산확률변수가 특정 값보다 작거나 같을 확률을 나타내는 함수
[연속확률분포 (Continous Probability Distribution)
- 확률변수 X가 실수와 같이 연속적인 값을 취할 때는 이를 연속확률변수라 하고 이러한 연속확률변수 X가 가지는 확률분포
기초통계7 : 연속확률분포
확률밀도함수 정규분포 지수분포 기타 연속확률분포 https://kurt7191.tistory.com/11?category=1000998 기초통계6 : 확률변수와 이산확률분포 확률변수와 확률분포 이변량 확률분포 이항분포 포아송분포 http
kurt7191.tistory.com
[확률밀도함수(PDF; Probability Density Function)]
- 연속확률변수의 분포를 나타내는 함수
[누적밀도함수(CDF; Cumulative Density Function)]
- 연속확률변수가 특정 값보다 작거나 같을 확률을 나타내는 함수
[최대우도법(Maximum Likehood Method)]
- 어떤 확률변수에서 표집한 값들을 토대로 그 확률변수의 모수를 구하는 방법
※ 관련 내용은 너무 길기 때문에, 하단 링크 참고
[확률/통계] 확률분포 총 정리 (이산확률분포, 연속확률분포)
통계에서 확률변수와 확률분포가 있다. 확률변수는 이산확률변수와 연속확률변수로 나뉘고, 마찬가지로 확률분포도 이산확률분포와 연속확률분포로 나뉜다. 이산의 대표적인 분포는 이항분포
roytravel.tistory.com
4. 표본분포
(1) 표본분포
- 모집단에서 추출한 일정한 개수의 표본에 대한 분포 상태
- 통계량에 의해 모집단에 있는 모수 추론
- 모집단: 정보를 얻고자 하는 대상 되는 집단 전체
- 모수: 모집단의 특성을 나타내는 대푯값
- 표본집단: 모집단에서 선택된 구성 단위의 일부
- 통계량: 표본에서 얻은 평균이나 표준오차와 같은 값 (이 값을 통해 모수를 추정하며, 무작위로 추출할 경우 각 표본에 따라 달라지는 확률변수)
(2) 표본 추출 방법
- 복원추출: 한 번 뽑은 표본을 모집단에 다시 넣고 추출하는 방식
- 비복원 추출: 한 번 뽑은 표본을 모집단에 다시 넣지 않고 추출하는 방식
(3) 표본조사 용어
- 표본: 조사하는 모집단의 일부분
- 표본조사: 모집단의 일부분을 조사하는 행위
- 표본오차: 모집단의 일부인 표본에서 얻은 자료를 통해 모집단 전체의 특성을 추론함으로써 생기는 오차 (표본의 크기에 반비례 → 표본의 크기가 증가하면 표본오차 작아짐)
- 비표본 오차: 표본 오차를 제외한 모든 오차 (부주의, 실수, 알 수 없는 원인 등)
- 표본 편의: 모수를 작게 또는 크게 할 때 추정하는 것과 같이 표본 추출 방법에서 기인하는 오차 (비표본 오차의 한 종류)
(4) 표본분포와 관련된 법칙
- 큰 수의 법칙: 데이터를 많이 뽑을수록 (n이 커질수록) 표본평균의 분산은 0에 가까워진다는 법칙 (데이터의 퍼짐이 적어져 정확해짐)
- 중심 극한 정리: 데이터의 크기가 커지면 그 데이터가 어떠한 형태이든 그 데이터 표본의 분포는 최종적으로 정규분포를 따른다는 법칙
이전글
다음글
'자격증 > 빅데이터분석기사' 카테고리의 다른 글
| [빅데이터 분석기사] 3과목 빅데이터 모델링(3-1) (0) | 2024.03.13 |
|---|---|
| [빅데이터 분석기사] 2과목 빅데이터 탐색(2-2-2) (0) | 2024.03.13 |
| [빅데이터 분석기사] 2과목 빅데이터 탐색(2-1-2) (0) | 2024.03.13 |
| [빅데이터 분석기사] 2과목 빅데이터 탐색(2-1-1) (0) | 2024.03.12 |
| [빅데이터 분석기사] 2과목 빅데이터 탐색(1-2) (0) | 2024.03.12 |



