[1과목]
★ 프라이버시 보호모델(비식별화 조치)
- k-익명성: 주어진 데이터 집합에서 같은 값이 적어도 k개 이상 존재하도록 하여 쉽게 다른 정보로 결합할 수 없게 하는 모델 ▶ 공개된 데이터에 대한 연결 취약성을 방어하나, 동질성 공격과 배경지식에 의한 공격에 취약
- l-다양성: 주어진 데이터 집합에서 함께 비식별 되는 레코드들은 적어도 l개의 서로 다른 민감한 정보를 가져야 하는 모델 ▶ 동질성 공격, 배경지식에 의한 공격을 방어하나, 쏠림 공격과 유사성 공격에 취약
- t-근접성: 동질 집합에서 특정 정보의 분포와 전체 데이터 집합에서 정보의 분포가 t이하의 차이를 보여야 하는 모델 ▶ 쏠림 공격과 유사성 공격을 방어
- m-유일성: 원본 데이터와 동일한 속성 값의 조합이 비식별 결과 데이터에 최소 m개 이상 존재하도록 함 ▶ 재식별 가능성 위험 낮춤
★ 차등프라이버시
▶ 데이터 세트에 임의로 노이즈를 삽입함으로써 개인정보가 제3자에게 노출되지 않도록 보호하는 기법
★ 가명처리 / 총계처리 / 데이터값 삭제 / 범주화 / 데이터 마스킹
| 가명처리 | 개념 | 개인 식별이 가능한 데이터에 대하여 직접 식별할 수 없는 다른 값으로 대체 |
| 장점 | 그 자체로는 완전 비식별화 가능하며 데이터의 변형, 변질수준 낮음 | |
| 단점 | 일반화된 대체 값으로 가명처리 함으로써 성명을 기준으로 하는 분석에 한계 존재 | |
| 총계처리 | 개념 | 개인정보에 대하여 통곗값을 적용하여 특정 개인을 판단할 수 없도록 하는 기법 |
| 장점 | 민감한 정보에 대하여 비식별화 가능하며 다양한 통계분석 데이터 세트 작성에 유리 | |
| 단점 | - 집계 처리된 데이터를 기준으로 정밀한 분석 어려움 - 집계 수량이 적을 경우 데이터 결합 과정에서 개인정보 추출 또는 예측 가능 - 총계처리 적용 시 개인정보 묶어서 관리 | |
| 데이터값 삭제 | 개념 | 개인정보 식별이 가능한 특정 데이터값 삭제 처리 방법 |
| 장점 | 민감한 개인 식별 정보에 대하여 완전한 삭제 처리가 가능하여 예측, 추론 등이 어려움 | |
| 단점 | 데이터 삭제로 인한 분석의 다양성, 분석 결과의 유효성, 분석정보의 신뢰성 저하 | |
| 범주화 | 개념 | 단일 식별 정보를 해당 그룹의 대푯값으로 변환 (범주화) 하거나, 구간 값으로 변환(범위화) 하여 고유 정보 추적 및 식별 방지 기법 |
| 장점 | 범주나 범위는 통계형 데이터 형식이므로 다양한 분석 및 가공 가능 | |
| 단점 | - 범주, 범위로 표현 됨에 따라 정확한 수치에 따른 분석, 특정한 분석결과 도출 어려움 - 데이터 범위 구간이 좁혀질 경우 추적 및 예측 가능 | |
| 데이터 마스킹 | 개념 | 개인 식별 정보에 대하여 전체 또는 부분적으로 대체 값으로 변환하는 기법 |
| 장점 | 완전 비식별화 가능, 원시 데이터의 구조에 대한 변형 적음 | |
| 단점 | - 과도한 마스킹 적용 시 필요한 정보로 활용하기 어려움 - 마스킹의 수준이 낮을 경우 특정한 값의 추적 예측 가능 |
★ 기술통계 종류
※ 기술 통계: 통계적 수치를 계산하고 도출하거나 시각화를 활용하여 데이터에 대한 전반적인 이해를 돕는 통계 기법.
데이터 분석 목적으로 수집된 데이터를 확률·통계적으로 정리·요약하는 기초적인 통계
기술 통계에서 기술은 Technology 가 아닌, Description
▶ 통계적 수치에는 대표값(평균, 중위수 등), 산포도(분산, 범위 등), 첨도, 왜도, 공분산, 상관계수 등이 있음. (가설검정은 추론통계에 속함)
▶ 상관분석 / 회귀분석 / 분산분석 / 주성분분석 / 판별분석
★ 탐색적 데이터 분석(EDA; Exploration Data Analyst): 수집한 데이터를 분석하기 전에 그래프나 통계적인 방법을 이용하여 다양한 각도에서 데이터의 특징을 파악하고 자료를 직관적으로 보는 분석 방법
※ 모형화: 분석 문제를 단순화하여 수치나 변수 사이의 관계로 정의하는 것
★ 개인정보 수집 및 이용 위해 정보주체의 동의를 받을 때 고지사항 (15조 2항)
▶ 개인정보 수집 및 이용 목적 / 수집하려는 개인정보의 항목 / 개인정보의 보유 및 이용 기간 / 동의를 거부할 권리가 있다는 사실 및 동의 거부에 따른 불이익이 있는 경우 그 불이익의 내용
★ (상향식 접근 방식) 프로세스 분석을 통한 기회 발굴 절차: 프로세스 분류 → 프로세스 흐름 분석 → 분석 요건 식별 → 분석 요건 정의
★ 분석 순위 우선 순위 평가
▶ 시급성: ROI 관점의 비즈니스 효과 (전략적 중요도와 KPI를 통한 목표 가치) 와 관련
▶ 난이도: ROI 관점의 투자비용 요소 (데이터 획득/저장/가공 비용, 분석 적용 비용, 분석 수준) 와 관련
★ 재현 데이터: 실제로 측정된 원본 자료를 활용하여 통계적 방법이나 기계학습 방법 등을 이용하여 새롭게 생성한 모의 데이터
- 원본 자료와 최대한 유사한 통계적 성질을 보이는 가상의 데이터를 생성하기 위하여 개인정보의 특성을 분석하여 새로운 데이터 생성
- 원본 자료와 다르지만, 원본 자료와 동일 분포를 따르도록 통계적으로 생성한 자료
- 모집단의 통계적 특성을 유지하면서도 민감한 정보를 외부에 직접 공개하지 않음
★ 빅데이터를 활용한 인공지능의 특징
- 상호보완 관계로 빅데이터는 인공지능 구현 완성도를 높여주고, 빅데이터는 인공지능을 통해 문제 해결 완성도를 높이게 됨
- 빅데이터를 통해 자체 알고리즘을 가지고 학습하는 딥러닝 기술을 활용할 수 있게 되었고, 특정 분야에서 인간의 지능을 뛰어넘는 능력을 갖추게 됨
- 빅데이터의 다양한 데이터를 스스로 학습하는 딥러닝 기술은 다양한 분야에서 상용화가 이루어지고 있음
- 빅데이터를 활용한 인공지능은 자체 알고리즘을 가지고 스스로 문제 해결 기준을 설정하여 학습
★ 데이터 사이언티스트가 데이터 엔지니어와 다르게 지녀야 하는 소양
- 머신러닝 모델을 사용해 정형, 비정형 데이터에서 인사이트 창출 능력
- 사내 데이터를 이용해서 고객 행동 패턴 모델링 진행, 패턴을 찾아내거나 이상치 탐지
- 예측 모델링, 추천 시스템 등을 개발해 비즈니스 의사결정에 필요한 인사이트 제공
※ 데이터 분석 및 활용에 사용될 소프트웨어 개발 능력은 데이터 엔지니어가 지녀야할 능력
★ 데이터 분야 직무별 업무
| 데이터 엔지니어 | - 비즈니스를 이해하고 대량의 데이터 세트를 가공하는 업무 - 분석 도구를 개발하고 대용량 데이터 분산 처리 시스템을 개발하는 업무 (하둡, 스파크 등 이용) - 시스템 개발에 필요한 프로그래밍 언어 사용 스킬 필수 |
| 데이터 분석가 | - 최적의 의사결정을 내리는 데 도움을 주는 비즈니스 인사이트를 제공하는 업무 - 데이터의 경향, 패턴, 이상값 등을 인식하기 위한 시각화 진행 및 보고서 작성 업무 - 각 팀의 전략을 수립하거나 업무 효율화에 필요한 데이터 수집 및 분석 |
| 데이터 사이언티스트 | - 머신러닝 모델을 사용해 정형, 비정형 데이터에서 인사이트를 창출하는 업무 - 사내 데이터를 이용해서 고객 행동 패턴 모델링 진행, 패턴을 찾아내거나 이상값 탐지 업무 |
| 데이터 아키텍트 | - 기업의 데이터 관리를 위한 청사진 만드는 업무 (데이터베이스 통합, 중앙 집중화, 보호 등) - 기업의 데이터를 하둡 기반의 비정형 DB로 이관 시 이관 프로세스 정립, 모니터링, 테스트 주도 |
★ 개인정보 보호 원칙
- 개인정보 처리자는 개인정보의 처리 목적에 필요한 범위에서 적합하게 개인정보를 처리하여야 하며, 그 목적 외의 용도로 활용하여서는 아니된다
- 개인정보 처리자는 개인정보의 익명 처리가 가능한 경우에는 익명에 의하여 처리될 수 있도록 하여야 한다
- 개인정보처리자는 수집된 개인정보를 필요한 목적에 의해서 활용하고, 그 이외에는 원칙적으로 정보 주체의 사생활 침해를 하지 말아야 한다
- 개인정보처리자는 개인정보의 처리 방법 및 종류 등에 따라 정보 주체의 권리가 침해받을 가능성과 그 위험 정보를 고려하여 개인정보를 안전하게 관리하여야 한다
★ 데이터 분석 업무
▶ 분석용 데이터 준비 / 텍스트 분석 / 탐색적 분석(EDA) / 모델링 / 모델 평가 및 검증 / 모델 적용 및 운영 방안수립
★ HDFS: 네임 노드는 삭제한 노드를 관리하는 기능 있음
★ 스파크: 인 메모리 기반의 실시간 데이터 처리와 관련된 오픈소스 프로젝트
★ 스크라이브: 대용량 실시간 로그 수집 기술
★ 공공 데이터 포맷
▶ JSON, XML, CSV
★ 빅데이터 분석 방법론의 분석 절차
▶ 분석 기획 → 데이터 준비 → 데이터 분석 → 시스템 구현 → 평가 및 전개
| 분석 기획 | 비즈니스 이해 및 범위 설정 / 프로젝트 정의 및 계획 수립 / 프로젝트 위험 계획 수립 / 수행 계획 수립 |
| 데이터 준비 | 필요 데이터 정의 / 데이터 스토어 설계 / 데이터 수집 및 정합성 검증 |
| 데이터 분석 | 분석용 데이터 준비 / 텍스트 분석 / EDA / 모델링 / 모델 평가 및 검증 / 모델적용 및 운영방안 수립 |
| 시스템 구현 | 설계 및 구현 / 시스템 테스트 및 운영 |
| 평가 및 전개 | 모델 발전 계획 수립 / 프로젝트 평가 보고 |
★ 빅데이터 분석 기획 절차
▶ 범위 설정 → 프로젝트 정의 → 위험 계획 수립 → 수행 계획 수립
★ CRISP-DM 분석 방법론
▶ 비즈니스의 이해를 바탕으로 데이터 분석 목적의 6단계로 진행되는 데이터 마이닝 방법론
1) 절차: 업무 이해 → 데이터 이해 → 데이터 준비 → 모델링 → 평가 → 전개
2) 구성 요소: 단계(Phase) / (일반화, 세분화) 태스크 / 프로세스 실행
★ API 게이트웨이
▶ 시스템의 전반에 위치하여 클라이언트로부터 다양한 서비스를 처리하고 내부 시스템으로 전달하는 미들 웨어
★ 고품질 데이터 속성
▶ 정확성, 시의성(적시성), 완전성, 일관성
★ 분산파일시스템
▶ 네트워크를 공유하는 여러 호스트 컴퓨터의 파일에 접근할 수 있게 하는 파일 시스템
★ 데이터 품질 진단 절차
품질 계획 수립 → 품질 기준 및 진단대상 정의 → 데이터 품질 측정 → 품질 측정 결과 분석 → 데이터 품질 개선
| 품질 계획 수립 | 프로젝트 정의, 조직 정의 및 편성, 품질진단절차 정의, 세부시행계획 확정 |
| 품질 기준 및 진단 대상 정의 | 품질 기준 선정, 품질 이슈 조사, 데이터 관리 문서 수집, 진단 대상 중요도 평가, 진단 대상 선정, 핵심 데이터 항목 정의, 데이터 프로파일링, 업무규칙 정의 |
| 데이터 품질 측정 | 데이터 품질 측정 수행, 품질지수 산출 |
| 품질 측정 결과 분석 | 오류 원인 분석, 주요 발생 사례 정리, 개선 방안 도출, 시급성과 우선순위 부여 |
| 데이터 품질 개선 | 품질 개선 계획 수립, 개선 진행 상황 모니터링, 조율 및 진행 관리, 수행 내역 및 결과 보고 |
[2과목]
★ 불균형 데이터 처리 - 과소 표집 / 과대 표집 / 임곗값 이동 / 비용 민간 학습 / 앙상블 기법
- 과소 표집: 많은 클래스의 데이터 일부만 선택하는 기법 (정보가 유실되는 단점) ▶ 기법: 랜덤 과소 표집, ENN, 토멕 링크 기법, CNN, OSS
- 과대 표집: 소수 데이터를 복제해서 많은 클래스의 양만큼 증가시키는 기법 (일반화 오류 발생) ▶ 기법: 랜덤 과대 표집, SMOTE, Borderline - SMOTE, ADASYN
- 임곗값 이동(경곗값 이동): 임곗값을 데이터가 많은 쪽으로 이동시키는 방법, 학습 단계에서는 변화 없이 학습하고 테스트 단계에서 임곗값 이동
- 앙상블 기법: 같거나 서로 다른 여러 가지 모형들의 예측/분류 결과를 종합하여 최종적인 의사 결정에 활용하는 기법 ▶ 배깅(랜덤포레스트), 부스팅(AdaBoost, GBM: 경사하강법)
- 클래스가 불균형한 관련 데이터를 그대로 이용할 경우 과대적합 문제 발생 가능
- 불균형 문제를 처리하지 않으면 모델은 가중치가 더 높은 클래스를 더 예측하려 하므로 정확도는 높아질 수 있으나, 분포가 작은 클래스의 재현율은 낮아지는 문제 발생 (분포가 작은 데이터의 정밀도와 재현율(민감도) 이 낮아지는 문제 발생)
- 불균형 데이터는 성능 평가를 위해 정밀도, 재현율, F1 지표, AUC 활용
★ 상자 수염
- IQR: Q3-Q1
- 수염은 Q1, Q3 로부터 IQR의 1.5배 내에 있는 가장 멀리 떨어진 데이터까지 이어진 선
- 이상값은 수염밖에 위치
- 상자 수염에 표시된 이상값을 통해 이상값의 처리 여부 판단 가능
★ 파생 변수 생성 방법
- 단위 변환: 주어진 변수의 단위 혹은 척도를 변환하여 새로운 단위로 표현
- 표현 형식 변환: 단순한 표현 방법으로 변환
- 요약 통계량 변환: 요약 통계량을 활용하여 생성
- 변수 결합: 다양한 함수 등 수학적 결합을 통해 새로운 변수 정의
★ 표본상관계수
▶ 두 변수 간에 직선 관계가 있는지 나타내는 통계량 (통계적 유의성 알 수 없음)
★ 주성분 분석 (PCA)
- 여러 변수 간에 내재하는 상관관계, 연관성을 이용해 소수의 주성분으로 차원 축소
- 상관관계가 있는 고차원 자료를 자료의 변동을 최대한 보존하는 저차원 자료로 변환하는 차원축소 방법
- 고윳값, 고유벡터를 통해 분석
- 주성분 분석의 목적 중 하나는 데이터를 이해하기 위한 차원 축소
- 제1주성분은 데이터의 변동을 최대로 설명해주는 방향에 대한 변수들의 선형 결합식 (데이터 분산이 가장 큰 방향에 대한 변수들의 선형 결합식)
- 변동이 큰 축을 기준으로 한 차원씩 선택
- 이산형 변수에 사용 가능
- 주성분 분석에서 누적 기여율이 70% ~ 90% 사이가 되는 주성분의 수로 결정
- 데이터간 높은 상관관계가 존재하는 상황에서 상관관계를 제거하여 분석의 용이성 증가
- 스크리 산점도의 기울기가 완만해지기 전까지 주성분의 수로 결정할 수 있다
- 차원 축소 시 변수 추출 방법 사용
- Eigen Decomposition, Singular Value Decompostion 을 이용한 행렬 분해 기법
- 수학적으로 직교 선형 변환으로 정의
- 차원 축소를 통해 원본 데이터 직관적으로 파악 어려움 (단점)
★ 표본 추출 종류
- 단순 무작위 추출: 모집단에서 정해진 규칙 없이 표본 추출 (표본의 크기 커질수록 정확도 높아지며, 추정값이 모수에 근접하므로 추정값 분산 감소)
- 계통 추출: 모집단을 일정한 간격으로 추출
- 층화 추출: 모집단을 여러 계층으로 나누고, 계층별로 무작위 추출 수행 (층내 - 동질적 / 층간 - 이질적)
- 군집 추출: 모집단을 여러 군집으로 나누고, 일부 군집의 전체 추출 (집단 내부 - 이질적 / 집단 외부 - 동질적)
★ 확률 분포 종류
▶ 이산확률분포: 포아송 분포, 베르누이 분포, 이항 분포, 초기하 분포
▶ 연속확률분포: 정규 분포, 표준정규분포(Z-분포), T-분포, 지수분포, F-분포, 카이제곱분포, 감마분포
★ T-분포 / F-분포 / Z-분포
▶ T-분포: 모집단이 정규분포라는 정도만 알고, 모표준편차는 모를 때 모집단의 평균을 추정하기 위해 사용. 표본의 크기가 작은 소표본에 사용
▶ F-분포: 모집단 분산이 서로 동일하다고 가정되는 두 모집단으로부터 표본의 크기가 각각 n1, n2인 독립적인 2개의 표본을 추출하였을 때 2개의 표본분산의 비율
▶ Z-분포: 표본 통계량이 표본평균일 때, 이를 표준화(정규화) 시킨 분포. 표본의 크기가 큰 대표본에 사용
★ 중심 극한 정리
▶ 표본의 개수가 커지면 모집단의 분포와 상관없이 표본분포는 정규분포에 근사
- 표본 크기 n이 충분히 클 때 만족
- 모집단의 분포는 연속형, 이산형 모두 가능 (모집단의 분포 형태에 관계 없이 성립)
- 표본의 크기인 n이 증가할수록 (보통 30이상) 평균이 μ이고 분산이 σ^2 (제곱) 인 모집단으로부터 확률적으로 독립인 표본을 추출하면 표본평균은 평균이 μ이고 분신이 σ^2/n 인 정규분포에 근사
★ Box-Cox 변환
▶ 데이터를 정규분포에 가깝게 만들기 위한 목적으로 사용 (변수 변환 가능, 로그 변환 포함)
★ H0: μ ≤ 35, H1: μ ≥ 35, 표본평균: 38, 모집단표준편차: 6, 표본개수: 36, 신뢰도 99%일 때, Z값과 귀무가설 검정
▶ Z값은 (38-35)/ 6/√36 = 3
▶ p-값은 세로축에서 3(Z값), 가로축에서 0.01 (유의수준) 찾음 → 0.9987 → 1-0.9987 = 0.0013
p-값이 유의수준 0.01 보다 낮으므로, 귀무가설 기각
★ 유의확률( p-값)
▶ 귀무가설이 참이라는 가정에 따라 주어진 표본 데이터를 희소 또는 극한값으로 얻을 확률
- p-값 > 유의수준 : 귀무가설 채택 / p-값 < 유의수준: 귀무가설 기각
- 유의수준(α): 제1종 오류를 범할 최대 확률
- 신뢰수준(1-α): 귀무가설이 참일 때 이를 참이라고 판단하는 확률
- 베타수준(β): 제2종 오류를 범할 최대 확률
- 검정력(1- β): 귀무가설이 참이 아닌 경우 이를 기각할 수 있는 확률
- 기각역: 귀무가설을 기각시키는 검정통계량의 범위
- 제1종오류: 귀무가설이 참인데 잘못하여 이를 기각하게 되는 오류
- 제2종오류: 귀무가설이 거짓인데 잘못하여 이를 채택하게 되는 오류
★ 평균
- 산술 평균: 자료를 모두 더한 후 자료 개수로 나눈 값
- 기하 평균: 숫자들을 모두 곱한 후 거듭 제곱근을 취해서 얻는 평균 (성장률, 백분율 등)
- 조화 평균: 자료의 역수에 대해 산술 평균을 구한 후 그것을 역수로 취한 평균 (평균 성장률, 속도의 평균 등)
★ 초기하분포
▶ 특정 그룹에서 뽑힌 표본의 수에 대한 확률 분포
- 시행 마다 성공 확률 일정치 않음 (각각의 시행 독립적이지 않음.)
- 이산 확률 분포 가짐
※ 각각의 시행이 독립적인 것은 이항 분포
★ 중위수는 3사분위수보다 항상 작음
★ 데이터 중에 큰 값이 있을 경우 사분위수들은 상대적으로 영향 거의 받지 않음
★ 혈압을 낮춰주는 약을 개발했을 때 효과가 있는지 검정을 할 때 사용하는 가설 검정
▶ 대응 표본(쌍체 표본) 단측 검정
대응 표본(쌍체 표본); 실험 전후의 연구 대상을 비교할 때 많이 사용되는 비교 방법
혈압이 기존 약보다 낮은지 여부를 판단하므로 단측 검정
| 단측 검정 | 모수에 대해 표본자료를 바탕으로 모수가 특정 값과 통계적으로 큰지 작은지 여부 판단 |
| 양측 검정 | 모수에 대해 표본자료를 바탕으로 모수가 특정 값과 통계적으로 같은지 여부 판단 |
★ 정규화
- 최소-최대 정규화는 이상값에 영향을 많이 받으므로 Z-점수 정규화 사용
- Quantile 정규화는 비교하려는 샘플들의 분포를 완전히 동일하게 만들고 싶을 때 사용
★ 피어슨 상관계수 행렬표에서 분석을 위해 제거해야 하는 변수
- 두 변수가 같이 커지거나 같이 작아지는 경향이 있으면 상관계수가 높음
- 상관계수가 높은 변수가 여럿 존재하면 파라미터 수가 불필요하게 증가하여 차원 저주에 빠질 우려가 있음
- 기계학습 모델 (선형 모델, 신경망 등)은 상관계수가 큰 예측 변수들이 있을 경우 성능이 떨어지거나 모델이 불안정해질 수 있으므로 상관계수가 큰 변수들 제거
★ 인코딩: 문자열 값들을 숫자형으로 변경하는 방식
※인코딩 종류: 원-핫 인코딩, 레이블 인코딩, 카운트 인코딩, 대상 인코딩
원-핫 인코딩: 표현하고 싶은 단어의 인덱스에 1의 값을 부여하고, 다른 인덱스에는 0을 부여하는 방식
레이블 인코딩: 범주형 변수의 문자열을 수치형으로 변환하는 방식
카운트 인코딩: 각 범주의 개수를 집계한 뒤 그 값을 인코딩하는 방식
대상 인코딩: 범주형 자료의 값들을 훈련 데이터에서 목표에 해당하는 값으로 바꿔주는 방식 (원-핫 인코딩의 변수의 값이 많아지는 문제를 해결)
[3과목]
★ 선형 회귀 모형 가정 중 잔차항(오차)과 관련 없는 것은 선형성
▶ 선형회귀 모형 가정: 선형성 / 독립성 / 등분산성 / 비상관성 / 정규성(정상성)
- 선형성: 독립변수와 종속변수가 선형적
- 독립성: 잔차와 독립변수 값은 서로 독립적
- 등분산성: 잔차가 고르게 분포
- 비상관성: 잔차가 서로 독립하면 비상관성
- 정규성: 잔차항이 정규분포를 이뤄야 함
★ 회귀 분석 유형
▶ 단순선형 회귀, 다중선형 회귀, 다항 회귀, 곡선 회귀, 로지스틱 회귀, 비선형 회귀
- 단순선형 회귀: 독립변수가 1개이며, 종속변수와의 관계가 직선
- 다중선형 회귀: 독립변수가 K개이며 종속변수와의 관계가 선형 (1차 함수)
- 다항 회귀: 독립변수와 종속변수와의 관계가 1차 함수 이상인 관계 (독립변수가 1개일 경우에는 2차 함수 이상)
- 곡선 회귀: 독립변수가 1개이며, 종속변수와의 관계가 곡선
- 로지스틱 회귀: 종속변수가 범주형인 경우 적용 (단순 로지스틱 회귀 및 다중, 다항 로지스틱 회귀로 확장 가능)
- 비선형 회귀: 회귀식의 모양이 미지의 모수들의 선형관계로 이뤄져 있지 않은 모형
★ TF-IDF / 토픽 모델링 (텍스트 마이닝 기법)
- TF-IDF: 텍스트마이닝에서 여러 문서로 이루어진 문서 군이 있을 때 어떤 단어가 특정 문서 내에서 얼마나 중요한 것인지 추출하는 기법
- 토픽 모델링: 기계학습 및 자연어처리 분야에서 토픽이라는 문서 집합의 추상적인 주제를 발견하기 위한 통계적 모델 중 하나. 텍스트 본문의 숨겨진 의미 구조를 발견하기 위해 사용되는 텍스트 마이닝 기법
★ 다차원 척도법
- 개체들 사이의 유사성, 비유사성을 측정하여 2차원 또는 3차원 공간상에 점으로 표현하여 개체들 사이의 집단화를 시각적으로 표현
- 스트레스 값이 0에 가까울수록 적합도 수준이 좋고, 1에 가까울수록 나쁨
- 위클리드 거리와 유사도 이용하여 구함
★ 데이터 분석 절차
▶문제 인식 → 연구조사 → 모형화 → 자료 수집 → 자료 분석 → 분석 결과 공유
★ 앙상블 기법: 예측력이 약한 모형을 연결하여 강한 모형으로 만드는 기법
- 배깅: 훈련 데이터에서 다수의 부트스트랩 자료를 주어진 자료에서 동일한 크기의 표본을 랜덤 복원 추출로 뽑은 자료
(편향이 낮은 과소적합 모델에 효과적 / 편향이 높은 과대적합 모델에 효과적)
- 부스팅: 가중치를 주어 표본을 추출하는 기법. 가중치를 활용하여 약 분류기를 강 분류기로 만드는 방법
※ 각 기법의 대표 알고리즘
배깅 - 랜덤 포레스트: 분류기 결합
부스팅 - AdaBoost: 잘못 예측한 데이터에 가중치 부여하여 오류 개선
- GBM: 경사하강법 이용
★ 앙상블에서 베이스 모형의 독립성을 최적화 하기 위한 방법
- 입력변수를 다양하게 함
- 서로 다른 알고리즘 사용
- 매개변수 다양하게 함
★ 베이즈 정리
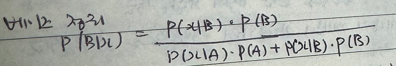
★ K-Fold / 홀드아웃(Holdout) / Dropout / Cross Validation
▶ K-Fold: 데이터 집합을 무작위로 동일 크기를 같은 k개의 부분 집합으로 나누고, 그 중 1개 집합은 평가 데이터로, 나머지 (K-1)개 집합은 훈련 데이터로 선정하여 분석 모형 평가. (K번 반복 수행. 결과를 K에 다수결 또는 평균으로 분석)
▶ Holdout: 비복원 추출 방법을 이용하여 랜덤하에 훈련 데이터와 평가 데이터로 나눠 검증
▶ Dropout: 인공신경망의 학습 과정에서 신경망 일부를 사용하지 않는 기법
▶ Cross Validation: 모델의 일반화 오차에 대해 신뢰할 만한 추정치를 구하기 위해 훈련, 평가 데이터를 기반으로 하는 검증 기법
★ 임베디드 기법
▶ 라쏘: 모든 가중치의 절댓값 합계 추가 (L1 노름 규제)
▶ 릿지: 모든 가중치의 제곱합 추가 (L2 노름 규제)
▶ 엘라스틱 넷: L1 규제, L2 규제 추가
★ 지도 학습 / 비지도 학습
- 지도 학습: 레이블이 알려진 학습 (주요 기법: 선형 회귀 분석, 로지스틱 회귀 분석 등)
- 비지도 학습: 레이블이 알려지지 않은 학습 (주요 기법: 군집 분석 등)
★ 독립변수 & 종속변수 유형별 분석 기법
- 독립변수: 연속형 + 종속변수: 연속형 ▶ 회귀분석, 인공신경망, K-NN(최근접이웃), 의사결정나무 (회귀)
- 독립변수: 연속형 + 종속변수: 이산형/범주형▶ 로지스틱 회귀분석, 판별 분석, K-NN, 의사결정나무 (분류)
- 독립변수: 이산형/범주형 + 종속변수: 연속형▶ 회귀분석, 인공신경망, 의사결정나무 (회귀)
- 독립변수: 이산형/범주형 + 종속변수: 이산형/범주형▶ 인공신경망, 의사결정나무 (분류), 로지스틱 회귀 분석
※ 꼭 들어감!
- 독립변수가 연속형이면 K-NN
- 독립변수가 이산형/범주형 이면 인공신경망
- 종속변수가 연속형이면 의사결정나무 (회귀)
- 종속변수가 이산형/범주형 이면 로지스틱 회귀 분석, 의사결정나무(분류)
★ 의사결정나무의 분석 과정
- 데이터의 분류 및 예측에 활용
- 부적절한 나뭇가지는 가지치기로 제거
- 이익, 위험, 비용 등을 고려하여 모형 평가
- 분석 목적과 자료 구조에 따라서 적절한 분리 기준과 정지 규칙 정하여 의사결정나무 생성
★ 로지스틱 회귀 분석
- 반응 변수를 1과 0으로 이진 분류하는 경우에 사용
- 반응 변수가 범주형일 경우 사용
- 반응 변수를 로짓으로 변환할 때 오즈(Odds) 사용
- 승산비를 로그 변환한 것이 로짓 함수
- 로짓 함수(반응 변수)의 값은 로그(로짓) 변환에 의해 음의 무한대부터 양의 무한대까지 값을 가짐
- 로지스틱 함수는 로짓 함수의 역함수
- 로지스틱 함수는 음의 무한대부터 양의 무한대까지의 값을 가지는 입력변수를 0부터 1사이의 값을 가지는 출력 변수로 변환한 것
★ 소프트맥수 함수
- 출력값이 여러 개로 주어지고 목표치가 다범주인 경우 각 범주에 속할 사후 확률 제공 함수
- 출력값은 0과 1 사이의 실수의 확률로 해석할 수 있음
- 출력값의 총합은 1
★ 활성화 함수: 순 입력합수로부터 전달받은 값을 출력값으로 변환해주는 함수
▶ 종류: 계단함수, 부호함수, 시그모이드 함수, tanh 함수, ReLU 함수, 소프트맥스 함수, Leaky ReLU 함수
- 하이퍼볼릭 탄젠스 (tahn) 함수는 -1에서 1의 값 가짐
- 부호함수는 임곗값을 기준으로 양의 부호 또는 음의부호 출력
- 계단함수는 임곗값을 기준으로 활성화 (y축 1) 또는 비활성화 (y축 0)
- 시그모이드 함수는 입력값이 0일 때, 미분값은 0.05
- ReLU 함수는 시그모이드의 기울기 소실 문제 해결
★ 비모수 통계: 평균이나 분산 같은 모집단의 분포에 대한 모수성을 가정하지 않고 분석
- 모집단의 분포에 대한 가정의 불만족으로 인한 오류의 가능성 작음
- 모수적 방법에 비해 통계량의 계산이 간편하여 직관적으로 이해 쉬움
- 이상값으로 인한 영향 적음
- 검정 통계량의 신뢰성 부족
★ SVM RBF (가우시안 RBF, SVM 에서 사용되는 커널 중 하나)
- 비선형 데이터가 있는 경우에 일반적으로 활용
- 데이터에 대한 사전 지식이 없는 경우 적절하게 분리할 때 활용
- 가장 많이 사용되는 커널
- 2차원의 점을 무한한 차원의 점으로 변환
▶ 그외 선형 커널 (기본 유형-1차원) / 다항 커널 (선형커널의 일반화 - 효율 적음) / 시그모이드 커널 (인공신경망의 다층 퍼셉트론 모델과 유사)
★ 요인분석
▶ 변수들 간의 상관관계를 고려한 분석방법
- 요인: 특정 현상에 영향을 미치는 중요한 인자
- 관측이 불가능 하나, 해석 가능
- 상관 계수가 높은 변수를 묶어 신규로 생성한 변수의 집합
★ 연관성 분석 측정 지표
| 지지도 | 전체 거래 중 항목 A와 B를 동시에 포함하는 거래의 비율 |
| 신뢰도 | A 상품을 샀을 때 B 상품을 살 조건부 확률에 대한 척도 |
| 향상도 | 규칙이 우연에 의해 발생한 것인지를 판단하기 위해 연관성의 정도를 측정하는 척도 - 향상도 =1: 서로 독립적 관계 - 향상도 > 1 양(+)의 상관관계 - 향상도 < 1 음(-)의 상관관계 |
★ 분산분석
▶ 두 개 이상의 집단의 평균 차이 검정
★ 윌콕슨 부호 순위 검정, 윌콕슨 순위 합 검정
- 윌콕슨 부호 순위 검정: 단일 표본 검정 기법
- 윌콕슨 순위 합 검정; 이변수 검정 기법
- 자료의 분포에 대한 대칭성 가정 필요
- 비모수적 방법
★ 자기 회귀 누적 이동평균 모형 (ARIMA)
- ARIMA 모형은 분기/반기/연간 단위로 다음 지표를 예측하거나 주간/월간 단위로 지표를 리뷰하여 트렌드를 분석하는 기법
- ARMA의 일반화 형태
- 백색 잡음은 독립적이고 동일한 분산 가짐
- 비정상 시계열 모형 ▶ 차분이나 변환을 통해 AR, MA, ARMA 모형으로 정상화 가능
- ARIMA (p, d, q)
▶ p: AR모형과 관련 있는 차수 / d: ARIMA에서 ARMA로 정상화활 때 차분 횟수 / q: MA모형과 관련 있는 차수
★ RNN 알고리즘
- 입력층, 은닉층, 출력층으로 구성되며 은닉층에서 재귀적인 신경망을 갖는 알고리즘
- 음성신호, 연속적 시계열 데이터 분석에 적합
- 장기 의존성 문제와 기울기 소실문제가 발생하여 학습이 이루어지지 않을수도 있음
- LTSM은 RNN의 장기의존성 문제를 보완하기 위해 설계한 신경망 알고리즘 (입력 / 망각 / 출력 게이트로 구성)
| 기울기 소실(GV; Gradient Vanishing) | 오차역전파 과정에서 입력층으로 갈수록 가중치에 따른 결과값의 기울기가 작아져 0에 수렴하는 문제 |
| 기울기 폭발(GE; Gradient Exploding) | 기울기가 점차 커지면서 가중치들이 비정상적으로 크게 업데이트 되는 문제 |
| 기울기 클리핑 | 기울기 폭발을 막기 위해 일정 임계값을 넘어서지 못하게 기울기 값을 자르는 방법 |
★ SNA (소셜 네트워크 분석)
▶ 개인과 집단 간의 관계를 노드와 링크로 그룹에 속한 사람들 간의 네트워크 특성과 구조를 분석하고 시각화하는 분석 기법
※ 중심성: 연결정도 중심성, 근접 중심성, 매개 중심성, 위세 중심성
[4과목]
★ ROC 커브: x축 - 거짓 긍정률(1-특이도) / y축 - 민감도
- AUC가 1.0에 가까울수록 분석 모형 성능 우수 / 0.5일 경우, 랜덤 선택에 가까운 성능
- 민감도 0, 특이도 1인 점 지님
- 민감도 1, 특이도 0인 점 지님
- 가장 이상적인 것은 민감도 1, 특이도 1일 때
- 가장 이상적으로 완벽한 분류 모형은 x축은 0, y축은 1일 때
- ROC 커브 밑부분 면적이 높을수록 좋은 모형으로 평가
- 그래프가 왼쪽 꼭대기에 가깝게 그려질수록 분류 성능 우수
- x축은 1-특이도, y축은 민감도
- 거짓긍정률과 참 긍정률을 통해 시각화한 그래프
- 민감도(=참 긍정률, TP Rate)를 세로 축으로, 특이도(=거짓 긍정률, FP Rate)를 가로축으로 사용
- ROC 곡선에서 거짓 긍정률과 참 긍정률은 어느 정도 비례 관계에 있음
★ F1-Score: 정밀도와 민감도를 하나로 합한 성능 평가 지표(0~1 사이의 범위)
- 정밀도와 민감도가 모두 클 때 F1-Score 도 큰 값
▶ 2* (정밀도*재현율) / (정밀도+재현율) ※ 재현율 = 민감도
★ 적합도 검정 기법: 표본 집단의 분포가 주어진 특정 이론을 따르고 있는지 검정하는 기법
- 자유도: (범주의 수)-1
- 적합도 검정의 자료를 구분하는 범주가 상호 배타적이어야 함
- 카이제곱 검정 기법의 유형에 속함
가정된 확률: 카이제곱 검정
정규성: 샤피로-윌크 / 콜모고로프-스미르노프
정규성(시각화): 히스토그램. Q-Q Plot
★ 히스토그램
- 양적 자료 표현에 사용
- 종속변수를 확률 단위로도 표현 가능
- 데이터 표현을 잘 하려면 구간을 잘 정해야 함
- 누적해서 표현하면 누적확률밀도함수 항상 가짐
★ 분석모형의 평가 방법
▶ 종속변수 유형에 따라 다름
- 종속변수가 범주형: 혼동행렬
- 종속변수가 연속형 : RMSE
- 종속변수가 범주형일 때 임곗값이 바뀌면 정분류율 변함
★ 혼동행렬
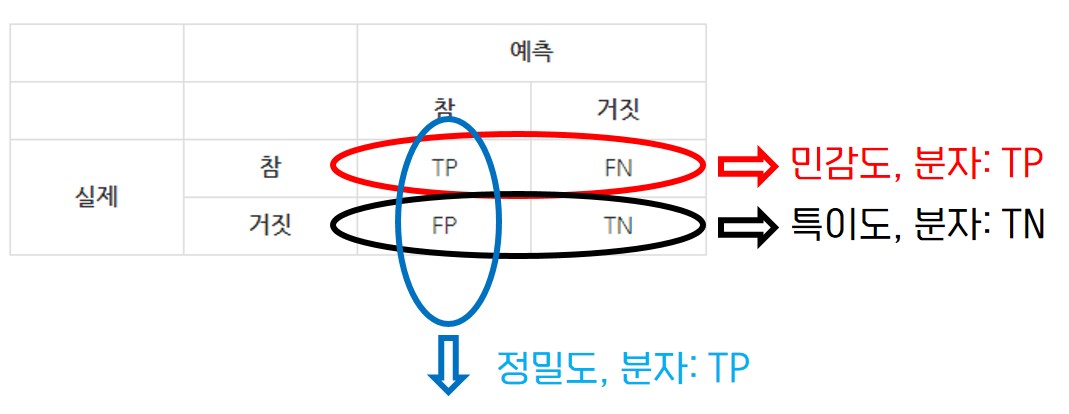

- 특이도: 실제로 '부정'인 범주 중에서 '부정'으로 올바르게 예측한 비율
- 민감도: 실제로 '긍정'인 범주 중에서 '긍정'으로 올바르게 예측한 비율
- 거짓긍정률(FPR): 실제로 '부정'인 범주 중에서 '긍정'으로 잘못 예측한 비율
- 정밀도: '긍정'으로 예측한 비율 중에서 실제로 '긍정'인 비율
★ 분석 모형 검증
- 데이터 수가 적으면 교차 검증 하는 것이 좋다
- 교차 검증을 통해 분석 모형의 일반화 성능 확인 가능
- 데이터 수가 많아서 검증 데이터가 많더라도 테스트 데이터로 성능 확인하는 과정 필요
★ 모형의 평가 기준
▶ 일반화의 가능성 / 효율성 / 예측과 분류의 정확성
★ 시계열 분해 그래프: 관측치를 통해 추세, 계절, 잔차(불규칙) 요인 확인 가능
▶ 예측은 확인 불가
구성요소 : 추세 요인, 계절 요인, 순환 요인, 불규칙 요인
★ 회귀 모형의 잔차가 등분산 가정을 만족하지 않은 경우
▶ 종속변수를 log로 변환하거나 WLS(Weighted Least Squre) 사용
★ 매개변수 / 초매개변수
▶ 매개변수(Parameter): 사람에 의해 수작업으로 측정되지 않음. 종종 학습된 모델의 일부로 저장됨.
▶ 초매개변수(Hyper Parameter): 데이터로부터 학습을 통해 얻어지는 것이 아닌 사용자가 직접 설정해주는 값. 모델의 알고리즘 구현 과정에서 사용
★ 왜도와 평균, 중위값, 최빈수 간의 관계
- 왜도 = 0, 좌우대칭, 평균 = 중위값 = 최빈수
- 왜도 > 0, 오른쪽으로 꼬리 김, 평균 > 중위값 > 최빈수
- 왜도 < 0, 왼쪽으로 꼬리 김, 평균 < 중위값 < 최빈수
▶ '영큰오평큰' 왜도가 0보다 크면 오른쪽으로 길고 평균이 가장 크다 라고 외우기!
★ 인공신경망의 과대적합 방지
- 가중치의 합 조절(규제 적용 - 라쏘, 릿지, 엘라스틱 넷)
- 학습률을 감소하는 방향으로 변경
- 설명 변수의 수 감소
- 데이터 세트 증강
- 모델의 복잡도 감소 (인공신경망의 은닉층 수 감소, 모델 수용력 낮춤)
- 드롭아웃 (신경망 일부 미사용)
★ 교차검증 (Cross Validation)
- 모델의 일반화 오차에 대해 신뢰할 만한 추정치를 구하기 위해 훈련, 평가데이터를 기반으로 하는 검증 기법
- 과대적합을 방지하는 데 활용될 수 있음
- 데이터의 모집단의 수가 적은 경우에 활용될 수 있음
- 훈련 / 검증 / 테스트용 데이터의 비율은 훈련용 데이터가 검증용, 테스트용 데이터보다 큰 비율로 지정
예) 훈련: 6 / 검증: 2 / 테스트: 2
★ 카이제곱
▶ 데이터의 분포와 사용자가 선택한 기대 또는 가정된 분포 사이의 차이를 나타내는 측정값
- 카이제곱 값이 클수록 귀무가설 기각
- 표본의 수가 많을수록 정규분포에 가까워짐
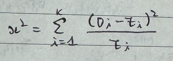
★ 데이터 시각화 절차(단계)
▶구조화 → 시각화 → 시각표현
| 구조화 | - 데이터 시각화 목표를 설정하고 분석 결과를 토대로 데이터의 표현 규칙과 패턴 탐색 - 시각화를 위한 요건을 정의한 후 사용자에 따른 시나리오를 작성하고 스토리를 구성 - 세부: 시각화 목표 설정 / 데이터 표현 규칙과 패턴 탐색 및 도출 / 시각화 요건 정의 / 사용자 시나리오 시각화 스토리 작성 |
| 시각화 | - 단순하고 명료한 메시지 전달을 위해 시각화 과정을 반복적으로 수행하여 시각화 - 구조화 단계에서 정의된 시각화 요건, 스토리를 기반으로 적절한 시각화 도구와 기술을 선택하여 데이터 분석 정보의 시각화를 구현 - 세부: 시각화 도구, 기술 선택 / 시각화 구현 |
| 시각표현 | - 시각화 단계에서 만들어진 결과물 보정 - 정보표현을 위한 그래픽 요소를 반영하여 그래픽 품질 향상 - 최종 시각화 결과물이 구조화 단계에서 정한 목적과 의도에 맞게 구현되었는지 확인 - 세부: 그래프 보정 / 전달 요소 강조 / 그래프 품질 향상 / 인터랙션 기능 적용 / 시각화 결과물 검증 |
★ 데이터 시각화 유형: 시간 / 분포 / 관계 / 비교 / 공간
| 시간 시각화 | 시간 흐름에 따른 변화를 통해 트렌드를 파악 ▶ 막대그래프, 누적 막대 그래프, 선 그래프, 영역 차트, 계단식 그래프, 추세선 |
| 분포 시각화 | 분류에 따른 변화를 최대, 최소, 전체 분포 등으로 구분 (전체에서 부분 간 관계 설명) ▶ 파이 차트, 도넛 차트, 트리맵, 누적 영역 차트 |
| 관계 시각화 | 집단 간의 상관관계를 확인하여 다른 수치의 변화 예측 ▶ 산점도, 산점도 행렬, 버블 차트, 히스토그램, 네트워크 그래프 |
| 비교 시각화 | 각각의 데이터 간의 차이점과 유사성 관계도 확인 ▶ 플로팅 바 차트, 히트맵, 체르노프 페이스, 스타 차트, 평행 좌표계 |
| 공간 시각화 | 지도를 통해 시점에 따른 경향, 차이 등을 확인 ▶ 등치 지역도, 등치선도, 도트 플롯맵, 버블 플롯맵, 카토그램 |
◆ 과목 또는 챕터별 상세 내용 공부가 필요하다면?
[빅데이터 분석기사] 시험 과목 및 주요 내용 (필기)
빅데이터 분석기사 (필기) 시험 과목 및 주요 내용 출처: 데이터자격검정 (dataq.or.kr) 필기과목명 주요항목 세부항목 1과목 빅데이터 분석 기획 빅데이터의 이해 빅데이터 개요 및 활용 빅데이터
puppy-foot-it.tistory.com
'자격증 > 빅데이터분석기사' 카테고리의 다른 글
| [빅분기 필기] (분노와 슬픔의) 시험 후기 (2) | 2024.04.06 |
|---|---|
| [빅분기 필기] 출제 빈도 높은 기출 오답 노트 (0) | 2024.04.04 |
| [빅데이터 분석기사] 4과목 기출문제 (1) | 2024.03.29 |
| [빅데이터 분석기사] 3과목 기출문제 (1) | 2024.03.29 |
| [빅데이터 분석기사] 2과목 기출문제 (1) | 2024.03.29 |
