기술 통계
평균, 중앙값, 모드, 차트, 종, 곡선을 계산하거나 데이터를 설명하기 위한 통계.
측정이나 실험에서 수집한 자료(data)의 정리, 요약, 해석, 표현 등을 통해 자료의 특성을 규명하는 통계적 방법
◆ 평균과 가중 평균
- 평균(mean): 어떤 값 집합을 평균한 값. 값을 모두 더한 다음, 값의 개수로 나누면 된다.
[파이썬으로 평균 계산하기]
# 파이썬으로 평균 계산하기
sample = [1, 3, 2, 5, 7, 0, 2, 3]
mean = sum(sample)/len(sample)
print(mean)
평균의 두 가지 버전인 표본 평균과 모집단 평균은 다음과 같이 표현한다.


※ ∑ (시그마) 는 모든 항목을 더한다는 의미이며, n과 N은 각각 표본과 모집단 크기를 나타내지만, 수학적으로 같은 의미(항목의 수)이다. 표본평균과 모집단평균 역시 계산은 동일하며 계산 대상이 표본인지 모집단인지에 따라 이름만 다를 뿐이다.
- 표본: 이상적으로는 무작위하고 편향되지 않은 집합. 표본을 사용해 모집단에 대한 속성을 추론한다. (모집단의 하위 집합)
- 모집단: 연구하고자 하는 특정 관심 그룹. 모집단 정의에는 경계가 있으며, 이러한 경계 중 일부는 광범위하며 넓은 지역이나 특정 연령대에 있는 대규모 그룹을 담는다. (예. '서울의 65세 이상의 모든 노인' 등)
- 가중 평균(weighted mean): 일반적으로 사용하는 평균은 각 값에 동일한 중요도를 부여한다. 하지만 아래와 같이 각 항목에 가중치를 다르게 부여하는 방식으로 평균을 구할 수도 있다.
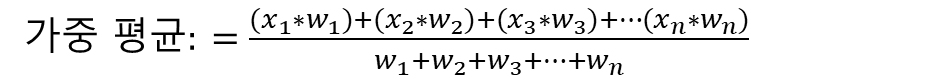
가중 평균은 일부 값이 다른 값보다 평균에 더 많이 기여하게 만드는 경우에 유용하다.
(예. 학업 시험에 가중치를 다르게 부여해 최종 성적을 매기는 것 - 중간 고사 20% 가중치, 기말고사 30%의 가중치 부여)
[파이썬에서 가중 평균 계산하기]
# 파이썬으로 가중 평균 계산하기
# 중간고사 가중치 0.2, 기말고사 가중치 0.3 (순서: 중간 기말 중간 기말)
sample = [90, 80, 63, 87]
weights = [0.20, 0.30, 0.20, 0.30]
weighted_mean = sum(s * w for s,w in zip(sample, weights)) / sum(weights)
print(weighted_mean)
※ zip() 함수는 입력으로 받은 반복 가능한 객체를 순회하면서 각 객체에서 원소를 하나씩 뽑아 만든 튜플을 반환한다.
◆ 중앙값
- 중앙값: 정렬된 값 집합에서 가장 가운데에 있는 값. 값을 순차적으로 정렬했을 때 가장 가운데에 있는 값.
※ 값의 갯수가 짝수일 경우에는 가장 가운데에 있는 두 값의 평균을 구한다.
[파이썬으로 중앙값 구하는 방법]
# 파이썬으로 중앙값 구하기
sample = [0, 1, 5, 7, 9, 10, 14]
def median(values):
ordered = sorted(values)
print('오름차순으로 정렬:', ordered)
n = len(ordered)
mid = int(n / 2) - 1 if n % 2 == 0 else int(n/2)
if n % 2 == 0:
return (ordered[mid] + ordered[mid+1]) / 2.0
else:
return (ordered[mid])
print('중앙값:', median(sample))
중앙값은 이상치(outlier) 또는 다른 값에 비해 매우 크거나 작은 값으로 인해 왜곡된 데이터에서 평균을 대신할 수 있는 유용한 대안이다. 중앙값은 이상치에 덜 민감하며 값의 정확한 위치가 아니라 상대적인 순서에 따라 데이터를 엄격하게 반으로 나눈다. 중앙값이 평균과 크게 차이나면 이상치로 인해 데이터셋이 왜곡되었다는 뜻이다.
※ 분위수(quantile)
기술 통계에는 분위수라는 개념이 있다. 중앙 이외에 다른 위치를 자르는 것만 제외하면 분위수 개념은 중앙값과 근본적으로 동일하다.
※ 사분위수(quartile)
데이터를 25% 단위로 잘라내는 분위수. 25%, 50%(중앙값), 75%
★ 이상치란 일반적인 데이터 분포를 따르지 않는 값으로, 다른 데이터와 차이가 매우 큰 값을 가진 데이터 포인트를 의미한다.
◆ 모드
- 모드: 가장 자주 발생하는 값 집합. 반복되는 데이터에서 가장 자주 발생하는 값을 찾을 때 유용.
두 번 이상 발생하는 값이 없으면 모드가 없는 것이다.
실전에서 모드는 데이터가 반복적이지 않는 한 많이 사용하지 않으며, 모드는 정수, 범주 및 기타 이산적인 변수에서 종종 볼 수 있다.
[파이썬에서 모드 계산하기]
# 파이썬으로 모드 계산하기
from collections import defaultdict
sample = [1, 3, 2, 5, 7, 0, 2, 3]
def mode(values):
counts = defaultdict(lambda: 0)
for s in values:
counts[s] += 1
max_count = max(counts.values())
modes = [v for v in set(values) if counts[v] == max_count]
return modes
print(mode(sample))
해당 데이터셋의 모드를 계산해보면 2와 3이 가장 많이 (그리고 동일하게) 발생하므로 바이모달임을 알 수 있다.
※ 바이모달 (bimodal): 두 값이 동일한 양의 빈도로 발생하는 것.
※ collections 모듈은 파이썬의 자료형(list, tuple, dict)들에게 확장된 기능을 주기 위해 제작된 파이썬의 내장 모듈이다.
표와 인덱싱 같은 데이터를 다룰 때 특히 유용하다.
※ defaultdict 는 딕셔너리의 서브 클래스로 첫 번째 매개변수에 존재하지 않는 키에 대한 딕셔너리 초깃값을 지정할 수 있다. 이 매개변숫값은 lambda와 같은 호출 가능한 객체여야 하며 기본값은 None이다.
◆ 분산과 표준 편차
- 분산 (variance): 데이터를 설명할 때 평균과 모든 데이터 포인트 간의 차이를 측정하는 경우가 많으며, 이를 통해 데이터가 얼마나 퍼져 있는지를 알 수 있다. 이러한 차이를 하나의 숫자로 축약해 데이터가 얼마나 퍼져 있는지 설명하는 방법.
각 데이터의 평균과의 차이를 제곱해서 더한 다음 차이를 제곱한 값의 평균을 구하는 방식으로 분산을 측정한다.
관측값에서 평균을 뺀 값을 제곱하고, 그것을 모두 더한 후 전체 개수로 나눠서 구한다. 즉, 차이값의 제곱의 평균이다.
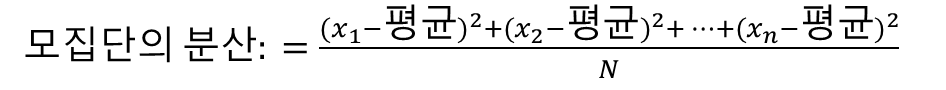
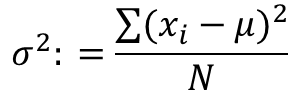
[파이썬으로 분산 계산하기]
# 파이썬으로 분산 계산하기
data = [0, 1, 5, 7, 9, 10, 14]
def variance(values):
mean = sum(values) / len(values)
_variance = sum((v - mean) **2 for v in values) / len(values)
return _variance
print(variance(data))
- 표준 편차(standard deviation): 분산을 제곱근한 것이다. 편차들(deviations)의 제곱합(SS, sum of square)에서 얻어진 값의 평균치인 분산의 성질로부터 다시 제곱근해서 원래 단위로 만들어줌으로써 얻게된다.
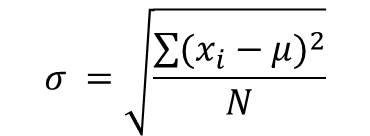
파이썬에서는 variance() 함수와 sqrt() 함수를 사용해 표준 편차를 구현할 수 있다.
[파이썬으로 표준 편차 계산하기]
# 파이썬으로 표준 편차 계산하기
from math import sqrt
data = [0, 1, 5, 7, 9, 10, 14]
def variance(values):
mean = sum(values) / len(values)
_variance = sum((v - mean) **2 for v in values) / len(values)
return _variance
def std_dev(values):
return sqrt(variance(values))
print(std_dev(data))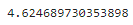
★ 표본의 분산과 표준 편차
앞서 설명한 분산과 표준 편차는 모집단이며,
이를 표본으로 계산할 때에는 공식이 조금 달라진다.
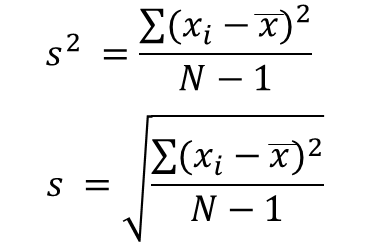
표본의 편향을 줄이고 표본에 기반한 모집단의 분산을 과소 평가하지 않기 위해 차이의 제곱 평균을 구할 때 총 항목수에서 -1을 한 값으로 나눈다.
[파이썬에서 표본의 표준 편차 계산]
# 파이썬에서 표본의 표준 편차 계산
from math import sqrt
data = [0, 1, 5, 7, 9, 10, 14]
def variance(values, is_sample: bool = False):
mean = sum(values) / len(values)
_variance = sum((v - mean) **2 for v in values) / (len(values) - (1 if is_sample else 0))
return _variance
def std_dev(values, is_sample: bool = False):
return sqrt(variance(values, is_sample))
print("분산 = {}".format(variance(data, is_sample=True)))
print("표준 편차 = {}".format(std_dev(data, is_sample=True)))
분산/표준 편차가 클수록 범위가 넓으므로 신뢰도가 떨어진다.
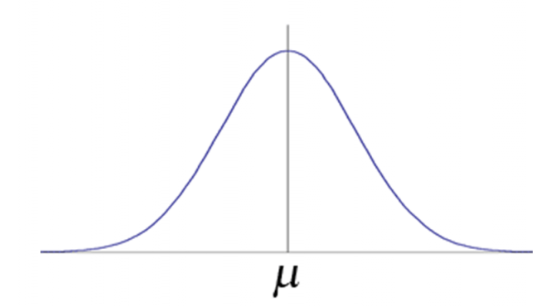
◆ 정규 분포
가우스 분포(Gaussian distribution) 라고도 알려진 정규 분포(normal distribution)는 평균 근처가 가장 질량이 크고 대칭 형태를 띤 종 모양의 분포이다.
이 분포의 퍼짐 정도는 표준 편차로 정의되며, 양쪽의 꼬리는 평균에서 멀어질수록 가늘어진다.
정규 분포는 자연, 공학, 과학 및 기타 다른 분야에서 많이 볼 수 있다.
예를 들어, 어느 중학교 학생 50명의 몸무게를 표본 추출한다고 가정해보자.
# 중학생 50명 몸무게
import pandas as pd
data = {
"몸무게 구간": ["57.4~57.9", "57.9 ~ 58.4", "58.4 ~ 58.9", "58.9 ~ 59.4", "59.4 ~ 59.9", "59.9 ~ 60.4",
"60.4 ~ 60.9", "60.9 ~ 61.4", "61.4 ~ 61.9", "61.9 ~ 62.4", "62.4 ~ 62.9", "62.9 ~ 63.4",
"63.4 ~ 63.9", "63.9 ~ 64.4", "64.4 ~ 64.9", "64.9 ~ 65.4", "65.4 ~ 65.9", "65.9 ~ 66.4",
"66.4 ~ 66.9", "66.9 ~ 67.4", "67.4 ~ 67.9", "67.9 ~ 68.4", "68.4 ~ 68.9", "68.9 ~ 69.4",
"69.4 ~ 69.9", "69.9 ~ 70.4"],
"인원 수": [1, 1, 0, 0, 1, 1, 4, 2, 1, 4, 1, 2, 2, 4, 1, 4, 5, 4, 1, 2, 3, 1, 1, 2, 2, 0]
}
# 데이터 프레임 생성
df = pd.DataFrame(data)
# 인원 수 합계
total = df['인원 수'].sum()
# 합계 행 추가
total_row = pd.DataFrame({
"몸무게 구간": ["합계"],
"인원 수": [total]
})
# 새로운 행 합치기
df_1 = pd.concat([df, total_row], ignore_index=True)
# 표 출력
print(df_1)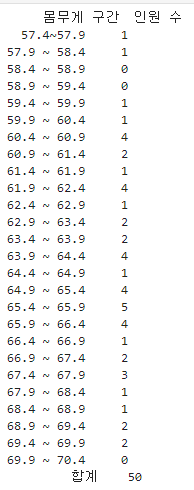
이를 시각화해 모집단에서 어떤 학생이 표본으로 추출될 가능성이 더 높은지 확인하려고 한다.
이때 사용할 수 있는 방법 중 한 가지 방법은 동일 크기의 범위로 값을 구간으로 묶는 히스토그램을 만든 다음, 각 범위 안에 속한 값이 개수를 표시하는 막대그래프를 그리는 것이다.
import matplotlib.pyplot as plt
# 히스토그램 그리기
plt.figure(figsize=(10, 6))
plt.bar(df['몸무게 구간'], df['인원 수'], color='skyblue')
plt.title('Weight Distribution of Middle School Students')
plt.xlabel('Weight Range (kg)')
plt.ylabel('Number of People')
plt.xticks(rotation=45)
plt.grid(axis='y')
# Show the plot
plt.tight_layout()
plt.show()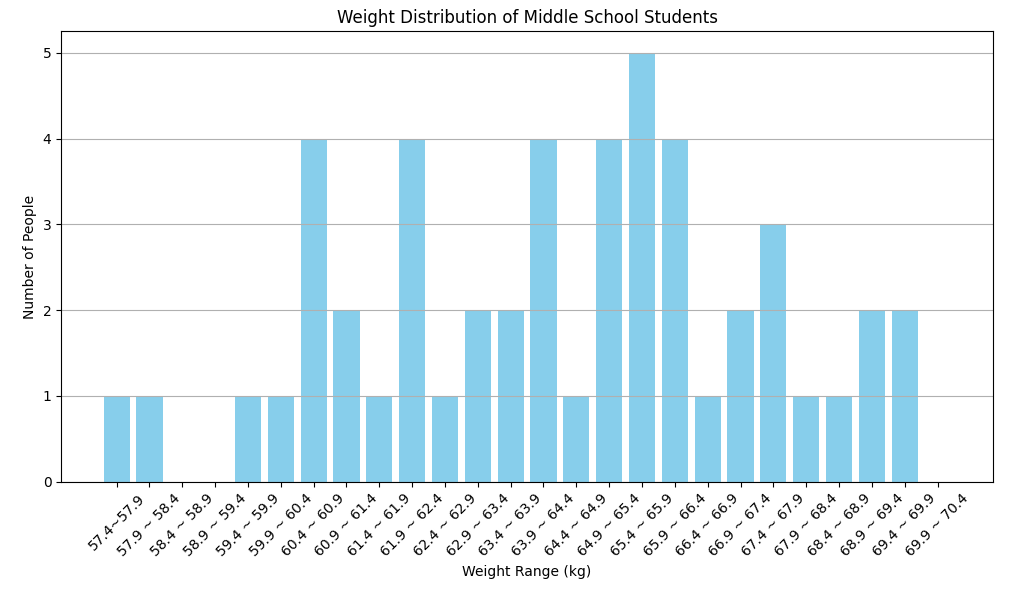
이 히스토그램의 경우, 구간이 너무 작기 때문에 데이터에서 의미 있는 형태를 드러내지 못한다. 따라서 구간을 더 크게 만들어야 한다.
구간을 3kg 으로 늘려서 만든 히스토그램
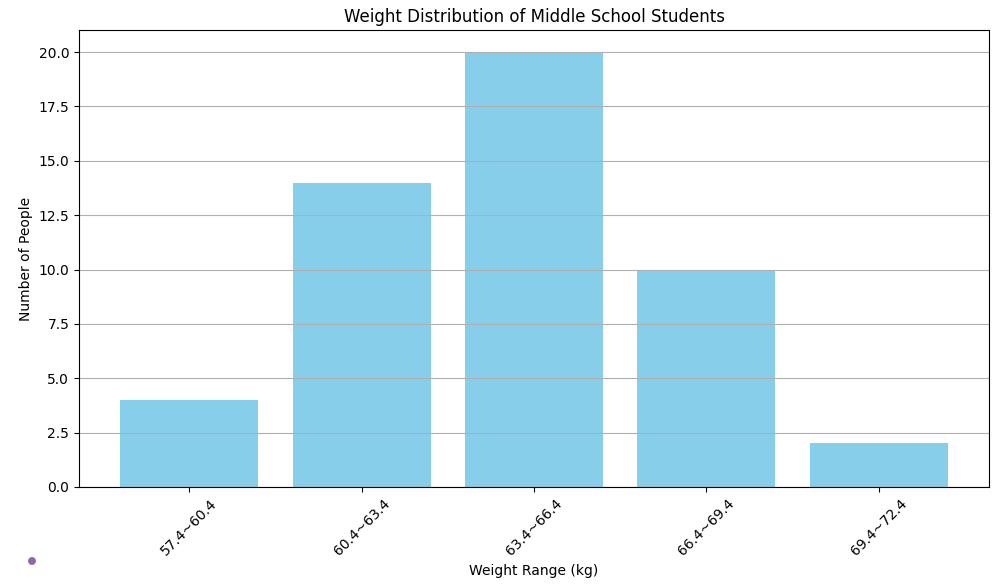
구간 크기를 적절하게 설정하면 데이터에 의미 있는 종 모양을 얻기 시작한다. 이는 표본이 정규 분포를 따른다는 증거일 가능성이 높다.
적절한 크기로 히스토그램을 만들고 확률 분포처럼 면적이 1.0이 되도록 규모를 조정하면 대략적인 종 모양 곡선을 볼 수 있다.
import seaborn as sns
from scipy.stats import norm
# 평균값과 표준편차 계산
mean = np.average(np.array([57.5, 58.2, 58.7, 59.2, 59.7, 60.2, 60.7, 61.2, 61.7, 62.2,
62.7, 63.2, 63.7, 64.2, 64.7, 65.2, 65.7, 66.2, 66.7,
67.2, 67.7, 68.2, 68.7, 69.2, 69.7, 70.2])) # 몸무게 범위 중앙값
std_dev = np.std(np.array([57.5, 58.2, 58.7, 59.2, 59.7, 60.2, 60.7, 61.2, 61.7, 62.2,
62.7, 63.2, 63.7, 64.2, 64.7, 65.2, 65.7, 66.2, 66.7,
67.2, 67.7, 68.2, 68.7, 69.2, 69.7, 70.2]))
# 정규 분포 곡선을 위한 x값 생성
x = np.linspace(mean - 4*std_dev, mean + 4*std_dev, 1000)
# Calculate the normal distribution (probability density function)
y = norm.pdf(x, mean, std_dev)
# 정규 분포 그리기
plt.figure(figsize=(10, 6))
plt.plot(x, y, color='skyblue', label='Normal Distribution')
plt.fill_between(x, y, alpha=0.2)
plt.title('Normal Distribution of Weight')
plt.xlabel('Weight (kg)')
plt.ylabel('Probability Density')
plt.axhline(0, color='black', lw=0.5)
plt.axvline(mean, color='red', linestyle='--', label='Mean')
plt.legend()
plt.grid()
# Show the plot
plt.tight_layout()
plt.show()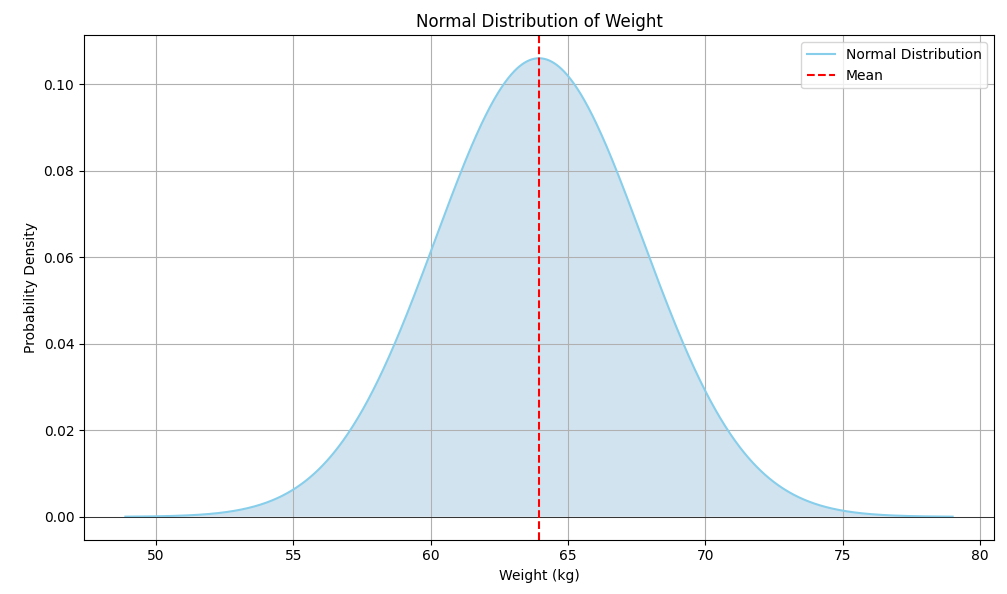
[정규 분포의 속성]
- 정규 분포는 대칭이다. 평균을 중심으로 양쪽이 거울에 반사된 것처럼 동일하다.
- 대부분의 질량은 평균 부근에 있다.
- 퍼짐 정도(좁거나 넓음)가 있으며 표준 편차로 이를 나타낸다.
- 꼬리는 가능성이 가장 낮은 부분이며 0에 수렴하지만 0이 되지는 않는다.
- 자연과 일상생활에서 일어나는 많은 현상과 유사하다.
확률 밀도 함수(PDF, probability density function)  |
[파이썬에서 정규 분포 함수 만들기]
# 파이썬에서 정규 분포 함수 만들기 (정규 분포는 가능도를 반환)
def normal_pdf(x: float, mean: float, std_dev: float) -> float:
return(1.0 / (2.0 * math.pi * std_dev **2) ** 0.5) * math.exp(-1.0 * ((x - mean) **2 / (2.0 * std_dev **2)))
누적 분포 함수(CDF, cumulative distribution function)
정규 분포에서 세로축은 확률이 아니라 데이터에 대한 가능도를 나타낸다. 확률을 얻으려면 주어진 범위의 곡선 아래 면적을 구해야 한다. 몸무게가 62~66kg 인 학생의 확률을 알고 싶을 때는 베타 분포와 마찬가지로 정규 분포의 CDF를 사용하면 된다.
CDF는 주어진 분포에 대해 주어진 x 값까지의 면적을 계산한다.
# CDF, PDF 그리기
# 중학생 50명 몸무게 정규 분포
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
from scipy.special import erf
# Data setup
data = {
"Weight range": ["57.4 ~ 57.9", "57.9 ~ 58.4", "58.4 ~ 58.9", "58.9 ~ 59.4", "59.4 ~ 59.9",
"59.9 ~ 60.4", "60.4 ~ 60.9", "60.9 ~ 61.4", "61.4 ~ 61.9", "61.9 ~ 62.4",
"62.4 ~ 62.9", "62.9 ~ 63.4", "63.4 ~ 63.9", "63.9 ~ 64.4", "64.4 ~ 64.9",
"64.9 ~ 65.4", "65.4 ~ 65.9", "65.9 ~ 66.4", "66.4 ~ 66.9", "66.9 ~ 67.4",
"67.4 ~ 67.9", "67.9 ~ 68.4", "68.4 ~ 68.9", "68.9 ~ 69.4", "69.4 ~ 69.9",
"69.9 ~ 70.4"],
"Number of people": [1, 1, 0, 0, 1, 1, 4, 2, 1, 4, 1, 2, 2, 4, 1, 4, 5, 4, 1, 2, 3, 1, 1, 2, 2, 0]
}
# Create a DataFrame
df = pd.DataFrame(data)
# 평균값과 표준편차 계산
mean = np.average(np.array([57.5, 58.2, 58.7, 59.2, 59.7, 60.2, 60.7, 61.2, 61.7, 62.2,
62.7, 63.2, 63.7, 64.2, 64.7, 65.2, 65.7, 66.2, 66.7,
67.2, 67.7, 68.2, 68.7, 69.2, 69.7, 70.2])) # 몸무게 범위 중앙값
std_dev = np.std(np.array([57.5, 58.2, 58.7, 59.2, 59.7, 60.2, 60.7, 61.2, 61.7, 62.2,
62.7, 63.2, 63.7, 64.2, 64.7, 65.2, 65.7, 66.2, 66.7,
67.2, 67.7, 68.2, 68.7, 69.2, 69.7, 70.2]))
# x값
x = np.linspace(mean - 4*std_dev, mean + 4*std_dev, 1000)
# Calculate PDF and CDF
pdf_value = norm.pdf(x, loc=mean, scale=std_dev)
cdf_value = norm.cdf(x, loc=mean, scale=std_dev)
# Plot PDF, CDF, and histogram
plt.plot(x, pdf_value, color='skyblue', label='PDF')
plt.plot(x, cdf_value, color='green', label='CDF')
# Labels and title
plt.xlabel('Weight (kg)')
plt.ylabel('Probability Density')
plt.title('Weight Distribution')
plt.legend()
plt.grid()
plt.show()
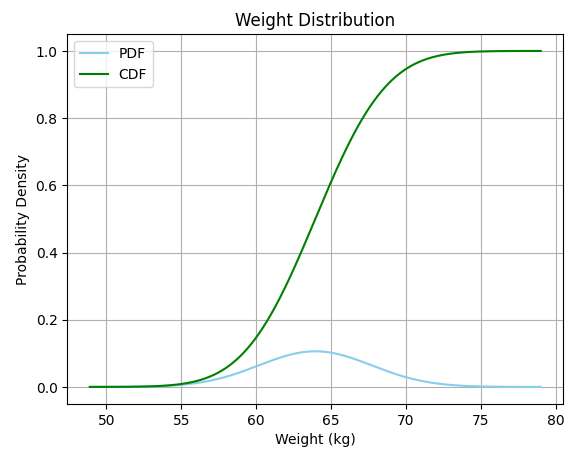
S자형 곡선(시그모이드 곡선)인 CDF는 해당 위치까지 PDF 면적을 나타낸다. 음의 무한대부터 평균까지의 면적에 해당하는 CDF 값은 0.5 또는 50%이다.
평균까지 면적이 0.5 또는 50%인 이유는 정규 분포의 대칭성 때문이다. 따라서 이 종 모양 곡선의 다른 쪽의 면적도 50%라고 예상할 수 있다.
사이파이를 사용해 평균까지의 면적을 계산하려면 norm.cdf() 함수를 사용하면 된다.
x = norm.cdf(mean, mean, std_dev)
print(x)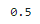
몸무게가 62~66kg 사이인 학생을 관측할 확률을 구하려면 66까지의 면적을 계산한 다음, 62까지의 면적을 빼면 되는데,
사이파이로 두 개의 CDF 연산을 빼면 된다.
x_1 = norm.cdf(66, mean, std_dev) - norm.cdf(62, mean, std_dev)
print(x_1)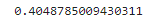
62~66kg 사이의 학생을 관찰할 확률은 0.404, 40.4% 이다.
역 CDF(inverse CDF)
예를 들어 학생의 95%가 속하는 몸무게를 찾고 싶을 경우, 역 CDF를 사용하면 이 작업을 쉽게 사용할 수 있다.
이는 CDF를 역방향으로 사용하는 것이므로 두 좌표축을 바꾸는 역 CDF를 사용한다.
x_2 = norm.ppf(0.95, mean, std_dev)
print('학생의 95%가 속하는 몸무게:', x_2)
학생의 95%가 70.13kg 이하임을 알 수 있다.
역CDF를 사용해 정규 분포를 따르는 난수(random number)도 생성할 수 있다. 학생의 몸무게 1,000개를 생헝하는 시뮬레이션을 만들려면 0.0에서 1.0 사이의 임의의 값을 생성해 역CDF에 전달한 다음, 몸무게 값을 반환하면 된다.
# 난수 생성하기
import random
for i in range(0, 1000):
random_p = random.uniform(0.0, 1.0)
random_weight = norm.ppf(random_p, mean, std_dev)
print("생성된 난수:", random_weight)
난수의 경우, numpy나 다른 라이브러리를 사용해 특정 분포를 따르는 난수를 생성할 수도 있다.
import numpy as np
random_weights = np.random.normal(mean, std_dev, size=1000)
print(random_weights)다음 내용
[개발자를 위한 수학] 기술 통계: z 점수(+파이썬)
기술 통계 이전 내용 [개발자를 위한 수학] 기술 통계: 평균, 분산, 정규 분포(+파이썬)기술 통계 평균, 중앙값, 모드, 차트, 종, 곡선을 계산하거나 데이터를 설명하기 위한 통계.측정이나 실
puppy-foot-it.tistory.com
[출처]
개발자를 위한 필수 수학
위키백과
DevHwi - 티스토리
Weekly I learned - 벨로그
실용 파이썬 프로그래밍: 프로그래밍 유경험자를 위한 강좌
윤영민 교수의 사유공간 블로그
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [개발자를 위한 수학] 추론 통계 (3) | 2024.10.06 |
|---|---|
| [개발자를 위한 수학] 기술 통계: z 점수(+파이썬) (0) | 2024.10.06 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.2) - 3 (2) | 2024.10.05 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.2) - 2 (0) | 2024.10.04 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.2) - 1 (0) | 2024.10.04 |



