★ 시작에 앞서 ★
해당 내용은 '<현대통계학-제6판>, 다산출판사, 2024' 에 나와있는 챕터별 연습문제를 교재를 응용하여 풀이하고, 수학적인 문제에 대한 답변을 파이썬으로 구현해보기 위해 작성하는 글이다.
해당 답변을 구현하는 방식은 답안지 없이 필자가 스스로 구현하는 것이므로, 정확한 (혹은 가장 효과적인) 답변이 아닐 수 있다. 이 글의 목적은 통계학 공부와 파이썬 프로그래밍 언어 공부를 동시에 하고자 함이며, 통계학을 공부하고 싶으신 분들은 해당 교재를 구매하는 것을 추천한다.
또한, 연습문제 번호 및 문제 내용은 필자가 임의대로 작성하였으며, 교재와는 다를 수 있다.
잘못된 부분이 있다면 언제든 피드백 부탁 드립니다! 감사합니다
챕터3 주요 개념: 중심경향(최빈값, 중앙값, 산술평균), 분산도(분산, 표준편차), 비대칭도
챕터3 연습문제1
다음 자료에서 산술평균, 중앙값, 최빈값을 구하라
[풀이]
# 산술평균, 중앙값, 최빈값(mode) 계산하기
from collections import defaultdict
number_1 = [3, 5, 2, 6, 5, 9, 5, 2, 8, 6]
number_2 = [51.6, 48.7, 50.3, 49.5, 48.9]
# 평균
mean_1 = sum(number_1)/len(number_1)
mean_2 = sum(number_2)/len(number_2)
# 중앙값
def median(values):
ordered = sorted(values)
n = len(ordered)
mid = int(n/2) - 1 if n % 2 == 0 else int(n/2)
if n % 2 == 0:
return (ordered[mid] + ordered[mid+1]) /2.0
else:
return (ordered[mid])
# 최빈값
def mode(values):
counts = defaultdict(lambda:0)
for s in values:
counts[s] += 1
max_count = max(counts.values())
modes = [v for v in set(values) if counts[v] == max_count]
return modes
# 답안
print('1번:', '평균:', mean_1, '중앙값:', median(number_1), '최빈값:', mode(number_1))
print('2번:', '평균:', mean_2, '중앙값:', median(number_2), '최빈값:', mode(number_2))
[평균, 중앙값, 최빈값(mode) 의 개념이 궁금하다면?]
[개발자를 위한 수학] 기술 통계: 평균, 분산, 정규 분포(+파이썬)
기술 통계 평균, 중앙값, 모드, 차트, 종, 곡선을 계산하거나 데이터를 설명하기 위한 통계.측정이나 실험에서 수집한 자료(data)의 정리, 요약, 해석, 표현 등을 통해 자료의 특성을 규명
puppy-foot-it.tistory.com
챕터3 연습문제2
각각 15, 20, 10, 18명으로 구성된 4개의 학급이 있다. 각 학급의 체중 평균이 63kg, 62kg, 66kg, 64kg 이라면 전체 학생들의 평균 체중은?
[풀이]
두 개 이상의 집단이 서로 다른 수치를 가졌을 때, 해당 집단을 합친 전체 집단의 평균은 일반 평균을 구하는 방법으로 계산하면 안 된다. 두 집단의 크기가 다르기 때문에 이런 경우는 각 집단의 크기를 가중치로 하여 평균을 계산해야 한다.
# 가중 평균 구하기
number = [63, 62, 66, 64] #몸무게 평균
weights = [15, 20, 10, 18] #학급 인원 수
weighted_mean = sum(s * w for s, w in zip(number, weights)) / sum(weights)
print('가중 평균:', weighted_mean)
챕터3 연습문제3
어느 공장근로자들의 추석상여금 분포표(단위: 만원)를 이용하여, 추석상여금의 산술평균, 중앙값, 최빈값을 구하라.
# 추석상여금 분포표 - 산술평균, 중앙값, 최빈값
import pandas as pd
data = {
"상여금(만원)" : ["118~126", "127~135", "136~144", "145~153", "154~162", "163~171", "172~180"],
"인원" : [3, 5, 9, 12, 5, 4, 2]
}
# 표 생성
df = pd.DataFrame(data)
print(df)
※ 최빈값(mode)은 양적 자료, 질적 자료에서 모두 쓰이나, 양적 자료의 연속형 자료의 경우에는 관찰값이 모두 다를 수 있다. 이때에는 최빈값은 없으나 자료를 등급으로 묶어서 각 등급에 해당되는 빈도수를 적는다면 가장 빈도수가 많은 등급이 최빈등급(modal class)가 되고, 같은 등급 안에서는 등급의 중간에 빈도수가 집중되어 있을 것이라는 가정하에 그 등급의 중간점이 최빈값이 된다.
import pandas as pd
from collections import defaultdict
# 데이터 생성
data = {
"상여금(만원)" : ["118~126", "127~135", "136~144", "145~153", "154~162", "163~171", "172~180"],
"인원" : [3, 5, 9, 12, 5, 4, 2]
}
# 표 생성
df = pd.DataFrame(data)
# 구간의 중간값을 계산하는 함수
def calculate_midpoint(range_str):
start, end = map(int, range_str.split('~'))
return (start + end) / 2
# 구간별 중간값 리스트 생성
bonus_midpoints = [calculate_midpoint(b) for b in data["상여금(만원)"]]
number_of_people = data["인원"]
# 산술평균 계산
mean = sum([m * n for m, n in zip(bonus_midpoints, number_of_people)]) / sum(number_of_people)
# 중앙값 계산 함수
def median(values, weights):
ordered_pairs = sorted(zip(values, weights))
cumulative_weight = sum(weights)
midpoint = cumulative_weight / 2
cumulative_sum = 0
for value, weight in ordered_pairs:
cumulative_sum += weight
if cumulative_sum >= midpoint:
return value
# 최빈값 계산 함수
def mode(values, weights):
counts = defaultdict(int)
for v, w in zip(values, weights):
counts[v] += w
max_count = max(counts.values())
modes = [v for v, count in counts.items() if count == max_count]
return modes
# 결과 출력
print('평균:', mean)
print('중앙값:', median(bonus_midpoints, number_of_people))
print('최빈값:', mode(bonus_midpoints, number_of_people))
<코드 풀이>
- 118~126"과 같은 문자열 구간을 숫자로 변환하여 평균 계산이 가능하도록 입력. 각 구간의 중간값을 사용하여 산술 평균 계산.
- bonus 리스트는 숫자형 값으로 변환하여 계산해야 하므로 구간의 중간값을 사용.
- 중앙값 계산 시 구간의 중간값 사용. (인원의 가중치 반영)
- 최빈값의 경우, 인원 수를 고려하여 상여금 구간에서 가장 많은 인원이 등장한 구간(최빈 등급) 반환.
챕터3 연습문제4
아래의 자료에서 범위, 산술평균, 평균편차, 표준편차, 분산을 구하라
※ 범위(range)
양극단의 두 수치가 얼마나 떨어져 있는가(분산도)를 살펴보는 방법. 관찰값들 중에서 가장 큰 수치와 가장 작은 수치의 차이다.
※ 평균편차(average deviation, AD)
평균편차는 관찰값과 산술평균과의 차이들의 평균이다.
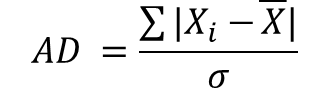
관찰값과 산술평균의 차이를 절대치를 사용해서 계산해야 한다.
# 범위, 산술평균, 평균편차, 표준편차, 분산 계산
import numpy as np
from math import sqrt
number_1 = [12, 6, 7, 3, 15, 10, 18, 5]
number_2 = [9, 3, 8, 8, 9, 8, 9, 18]
# 범위구하기
range_1 = max(number_1) - min(number_1)
range_2 = max(number_2) - min(number_2)
# 산술평균
mean_1 = np.mean(number_1)
mean_2 = np.mean(number_2)
# 절대편차 구하기
absolute_deviation_1 = [abs(x - mean_1) for x in number_1]
absolute_deviation_2 = [abs(x - mean_2) for x in number_2]
# 평균편차 구하기
average_deviation_1 = np.mean(absolute_deviation_1)
average_deviation_2 = np.mean(absolute_deviation_2)
# 분산
def variance(values):
mean = sum(values) / len(values)
_variance = sum(( v - mean)**2 for v in values) / len(values)
return _variance
# 표준편차
def std_dev(values):
return sqrt(variance(values))
# 답안
print('1:', '범위:', range_1, '평균:', mean_1, '평균편차:', average_deviation_1, '표준편차:', std_dev(number_1), '분산:', variance(number_1))
print('2:', '범위:', range_2, '평균:', mean_2, '평균편차:', average_deviation_2, '표준편차:', std_dev(number_2), '분산:', variance(number_2))
챕터3 연습문제5
다음은 10명의 학생들에게 실시한 검사의 정답 수를 세어 본 결과다. 이 자료에서 분산과 표준편차, 비대칭도를 구하라.
※ 비대칭도: 관찰값들이 어느 쪽으로 치우쳐 있는가를 말하는 것. (왜도, skewness)
도수분포표에서 비대칭도를 조사하려면 중심경향값인 산술평균과 중앙값을 비교해 보면 된다.
- 완전히 대칭상태인 분포에서는 산술평균과 중앙값이 일치한다.
- 왼쪽꼬리분포에서는 평균이 중앙값보다 작게 된다. 평균-중앙값은 음(-)의 값을 갖는다.
- 오른쪽꼬리분포에서는 평균-중앙값이 양(+)의 값을 갖게 된다.
▶ 데이터세트의 왜곡(비대칭성)을 계산하려면 Python의 scipy.stats 모듈을 사용할 수 있다
※ 중심경향(central tendency; 집중경향)은 모집단 혹은 표본으로부터 얻어진 자료를 도표화 하면 많은 자료가 어떤 특정한 값으로 몰리는 현상. 자료를 대표하는 값이며, 가로축의 양쪽으로부터 어느 한 점을 중심으로 모이는 경향이다.
[풀이]
# 검사의 정답 수: 분산과 표준편차, 비대칭도
import numpy as np
from math import sqrt
from scipy.stats import skew
correct = [3, 5, 7, 8, 9]
person = [2, 3, 2, 2, 1]
# 가중 평균 (Weighted Mean)
def weighted_mean(values, weights):
return sum(v * w for v, w in zip(values, weights)) / sum(weights)
# 가중 표준편차 (Weighted Standard Deviation)
def weighted_std_dev(values, weights):
return sqrt(weighted_variance(values, weights))
# 가중 분산 (Weighted Variance)
def weighted_variance(values, weights):
mean = weighted_mean(values, weights)
variance = sum(w * (v - mean)**2 for v, w in zip(values, weights)) / sum(weights)
return variance
# 비대칭도
# 두 데이터 결합
data = []
for i in range(len(correct)):
data.extend([correct[i]] * person[i])
# 비대칭도(왜도) 계산
asymmetry = skew(data)
# 결과 출력
print("가중 표준편차:", weighted_std_dev(correct, person))
print("가중 분산:", weighted_variance(correct, person))
print("왜도:", asymmetry)
챕터3 연습문제6
한 학급의 통계학 시험점수를
1) 도수분포표로 정리하라 (시험점수 / 빈도)
2) 시험점수의 산술평균, 중앙값, 최빈값을 각각 구하라
3) 분산과 표준편차를 구하라
4) 피어슨의 비대칭도(Sk)를 구하라
※ 피어슨의 비대칭도(Pearson's coefficient of skewness, Sk):
산술평균과 중앙값의 차이가 표준편차에 비하여 얼마나 떨어져 있는가를 나타낸다. 비대칭도를 측정하는 방법으로 많이 쓰인다.

[풀이1 - 도수분포표 생성]
# 통계학 시험점수
import numpy as np
from math import sqrt
from scipy.stats import skew
import pandas as pd
# 데이터 생성
data = {
"점수" : ["50~59", "60~69", "70~79", "80~89", "90~99"],
"인원" : [2, 12, 26, 15, 5]
}
df = pd.DataFrame(data)
# "점수"를 인덱스로 설정
df.set_index("점수", inplace=True)
# 결과 출력
print(df)
[풀이2 - 산술평균, 중앙값, 최빈값]
# 구간의 중간값을 계산하는 함수
def calculate_midpoint(range_str):
start, end = map(int, range_str.split('~'))
return (start + end) / 2
# 구간별 중간값 리스트 생성
score_midpoints = [calculate_midpoint(b) for b in data["점수"]]
number_of_people = data["인원"]
# 산술평균 계산
mean = sum([m * n for m, n in zip(score_midpoints, number_of_people)]) / sum(number_of_people)
# 중앙값 계산 함수
def median(values, weights):
ordered_pairs = sorted(zip(values, weights))
cumulative_weight = sum(weights)
midpoint = cumulative_weight / 2
cumulative_sum = 0
for value, weight in ordered_pairs:
cumulative_sum += weight
if cumulative_sum >= midpoint:
return value
# 최빈값 계산 함수
def mode(values, weights):
counts = defaultdict(int)
for v, w in zip(values, weights):
counts[v] += w
max_count = max(counts.values())
modes = [v for v, count in counts.items() if count == max_count]
return modes
# 결과 출력
print('평균:', mean)
print('중앙값:', median(score_midpoints, number_of_people))
print('최빈값:', mode(score_midpoints, number_of_people))
[풀이3 - 분산과 표준편차, 피어슨 비대칭도]
먼저, 앞의 코드를 활용하여 각 점수의 구간별 중앙값을 구한다.
# 구간별 중간값 리스트 생성
score_midpoints = [calculate_midpoint(b) for b in data["점수"]]
print(score_midpoints)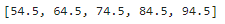
각 구간별 중앙값을 이용하여 나머지 지표를 계산한다.
import numpy as np
from math import sqrt
# 각 점수의 중앙값 (scores)과 인원수 (number_of_people)
scores = [54.5, 64.5, 74.5, 84.5, 94.5]
number_of_people = [2, 12, 26, 15, 5]
# 가중 평균 (Weighted Mean)
def weighted_mean(values, weights):
return sum(v * w for v, w in zip(values, weights)) / sum(weights)
# 가중 분산 (Weighted Variance)
def weighted_variance(values, weights):
mean = weighted_mean(values, weights)
variance = sum(w * (v - mean)**2 for v, w in zip(values, weights)) / sum(weights)
return variance
# 가중 표준편차 (Weighted Standard Deviation)
def weighted_std_dev(values, weights):
return sqrt(weighted_variance(values, weights))
# 산술 평균
mean_value = weighted_mean(scores, number_of_people)
# 피어슨 비대칭도
sk = (3 * (mean_value - 74.5)) / weighted_std_dev(scores, number_of_people)
# 결과 출력
print("가중 표준편차:", weighted_std_dev(scores, number_of_people))
print("가중 분산:", weighted_variance(scores, number_of_people))
print("피어슨 비대칭도:", sk)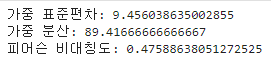
[최종 - 전체코드 결합]
연습문제6의 풀이2, 3을 결합한 코드는 다음과 같다.
# 통계학 시험점수 - 모든 코드 결합(도수분포표 제외)
# 통계학 시험점수
import numpy as np
from math import sqrt
from scipy.stats import skew
import pandas as pd
# 데이터 생성
data = {
"점수" : ["50~59", "60~69", "70~79", "80~89", "90~99"],
"인원" : [2, 12, 26, 15, 5]
}
df = pd.DataFrame(data)
# "점수"를 인덱스로 설정
df.set_index("점수", inplace=True)
# 구간의 중간값을 계산하는 함수
def calculate_midpoint(range_str):
start, end = map(int, range_str.split('~'))
return (start + end) / 2
# 구간별 중간값 리스트 생성
score_midpoints = [calculate_midpoint(b) for b in data["점수"]]
number_of_people = data["인원"]
# 산술 평균
mean_value = weighted_mean(scores, number_of_people)
# 중앙값 계산 함수
def median(values, weights):
ordered_pairs = sorted(zip(values, weights))
cumulative_weight = sum(weights)
midpoint = cumulative_weight / 2
cumulative_sum = 0
for value, weight in ordered_pairs:
cumulative_sum += weight
if cumulative_sum >= midpoint:
return value
# 최빈값 계산 함수
def mode(values, weights):
counts = defaultdict(int)
for v, w in zip(values, weights):
counts[v] += w
max_count = max(counts.values())
modes = [v for v, count in counts.items() if count == max_count]
return modes
# 각 점수의 중앙값 (scores)
mid_scores = score_midpoints
# 가중 평균 (Weighted Mean)
def weighted_mean(values, weights):
return sum(v * w for v, w in zip(values, weights)) / sum(weights)
# 가중 분산 (Weighted Variance)
def weighted_variance(values, weights):
mean = weighted_mean(values, weights)
variance = sum(w * (v - mean)**2 for v, w in zip(values, weights)) / sum(weights)
return variance
# 가중 표준편차 (Weighted Standard Deviation)
def weighted_std_dev(values, weights):
return sqrt(weighted_variance(values, weights))
# 피어슨 비대칭도
sk = (3 * (mean_value - median(score_midpoints, number_of_people))) / weighted_std_dev(scores, number_of_people)
# 결과 출력
print('평균:', mean_value)
print('중앙값:', median(score_midpoints, number_of_people))
print('최빈값:', mode(score_midpoints, number_of_people))
print("가중 표준편차:", weighted_std_dev(scores, number_of_people))
print("가중 분산:", weighted_variance(scores, number_of_people))
print("피어슨 비대칭도:", sk)
다음 내용
[파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.3)-2
★ 시작에 앞서 ★ 해당 내용은 ', 다산출판사, 2024' 에 나와있는 챕터별 연습문제를 교재를 응용하여 풀이하고, 수학적인 문제에 대한 답변을 파이썬으로 구현해보기 위해 작성하는 글이다.해
puppy-foot-it.tistory.com
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [개발자를 위한 수학] 선형대수학: 벡터, 선형변환 (1) | 2024.10.07 |
|---|---|
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.3)-2 (1) | 2024.10.07 |
| [개발자를 위한 수학] 추론통계: 가설 검정 (+파이썬) (0) | 2024.10.06 |
| [개발자를 위한 수학] 추론 통계 (3) | 2024.10.06 |
| [개발자를 위한 수학] 기술 통계: z 점수(+파이썬) (0) | 2024.10.06 |



