★ 시작에 앞서 ★
해당 내용은 '<현대통계학-제6판>, 다산출판사, 2024' 에 나와있는 챕터별 연습문제를 교재를 응용하여 풀이하고, 수학적인 문제에 대한 답변을 파이썬으로 구현해보기 위해 작성하는 글이다.
해당 답변을 구현하는 방식은 답안지 없이 필자가 스스로 구현하는 것이므로, 정확한 (혹은 가장 효과적인) 답변이 아닐 수 있다. 이 글의 목적은 통계학 공부와 파이썬 프로그래밍 언어 공부를 동시에 하고자 함이며, 통계학을 공부하고 싶으신 분들은 해당 교재를 구매하는 것을 추천한다.
또한, 연습문제 번호 및 문제 내용은 필자가 임의대로 작성하였으며, 교재와는 다를 수 있다.
잘못된 부분이 있다면 언제든 피드백 부탁 드립니다! 감사합니다
이전 내용
[파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.6)-2
★ 시작에 앞서 ★ 해당 내용은 ', 다산출판사, 2024' 에 나와있는 챕터별 연습문제를 교재를 응용하여 풀이하고, 수학적인 문제에 대한 답변을 파이썬으로 구현해보기 위해 작성하는 글이다.해
puppy-foot-it.tistory.com
챕터 7 주요 내용
- 연속확률분포: 길이, 속도, 무게, 부피 등 일정범위 내에서 어떠한 실숫값이라도 취할 수 있는 연속확률변수의 확률분포.
연속형 확률분포는 높이가 아니라 면적으로 확률을 나타내게 된다.
- 균일분포(uniform distribution): 확률변수가 취하는 모든 구간에서 각 사건의 발생확률이 일정하다.

- 정규분포 (또는 가우스분포, Gaussian distribution): 연속확률분포 중 가장 널리 이용되는 분포. 표본을 통한 통계적 추정 및 가설검정이론의 기본이 된다.
정규곡선(normal curve)으로부터 유래한 분포로서 19세기 초 가우스가 물리계측의 오차를 계산하는 과정에서 도입된 확률분포이다.
정규분포는 평균과 표준편차에 의해 결정되므로 정규분포의 모양은 다양하다. 따라서 분포족 혹은 분포모임(a family of distributions) 으로도 불린다. 그러므로 계산 시마다 특정한 정규분포마다 확률밀도함수를 이용하여 계산한다는 것이 번거롭고 매우 어렵기 때문에, 수많은 가능한 정규분포에 모두 적용할 수 있는 표준정규분포를 이용하여 분포의 모양을 통일한 다음, 확률을 계산하는 방식으로 사용한다.
[정규분포의 특성]
- 정규분포의 모양과 위치는 분포의 평균과 표준편차로 결정된다
- 정규분포의 확률밀도함수는 평균(𝜇)을 중심으로 대칭인 종모양이다.
- 정규곡선은 X축에 맞닿지 않으므로 확률변수 X가 취할 수 있는 값의 범위는 -oo < X < +oo 이다
- 분포의 평균(𝜇)과 표준편차(𝜎)가 어떤 값을 갖더라도, 정규곡선과 X축 사이의 전체 면적은 1이다.
[정규분포의 확률밀도함수]

- 표준정규분포(standard normal distribution, Z-분포): 표준정규분포는 모든 정규분포를 평균 𝜇=0, 표준편차 𝜎=1 이 되도록 표준화한 것이다. 어떤 확률변수 X의 관찰값이 그 분포의 평균으로부터 표준편차의 몇 배 정도나 떨어져 있는가를 다음과 같이 표준화된 확률변수 Z로 나타내기 때문에 Z-분포라고도 한다.

표준화된 정규분포를 이용하면 각 확률변수 간의 비교뿐만 아니라 정규분포에서의 특정한 면적의 확률을 계산할 때도 편리하다.
표준정규분포가 중요한 이유는 제각기 다른 정규분포라 하더라도 이를 표준정규분포로 표준화하였을 경우 Z값이 일치하면 그때의 확률이 모두 같다는 데 있다.
그러므로 모든 정규분포에서 넓이의 계산, 즉 확률의 계산은 표준정규분포의 Z값에 따른 넓이만 알면 되며, 이 넓이를 표로 만든 것이 표준정규분포표이다. (Z값은 추론통계에서 가장 많이 사용되고 있다.)

[표준정규분포표 확인 - 출처: 전북특별자치도교육청]
표준정규분포표 보는 법
Z = 1이 0.3413 ▶ Z=0에서 Z=1 사이의 넓이가 0.3413 이라는 것을 뜻한다.
Z = 1.04 에서 0.3508 ▶ Z=0에서 Z=1.04 사이의 넓이가 전체 면적의 35.08% 를 차지한다는 뜻이다.
만약, Z값이 1과 2 사이에 있을 확률을 알고 싶다면
- Z=0과 Z=2 사이의 면적을 구한다 (1)
- Z=0과 Z=1 사이의 면적을 구한다 (2)
- (1)의 면적에서 (2)의 면적을 뺀다
0.4772 - 0.3413 = 0.1359
[특정 Z 값 사이에 있을 확률 계산법]
Q1. Z=-1 ~ Z=1 사이에 확률변수가 있을 확률
P(-1≤Z ≤0) + P(0 ≤Z ≤1)
= 2 * P(0 ≤Z ≤1)
= 2 * 0.3413
= 0.6826
Q2. Z=-2 보다 작거나 Z=2 보다 큰 사이에 확률변수가 있을 확률
P(Z ≤-2) + P(Z≥+2)
= 1 - P(-2 ≤Z ≤=2)
= 1 - 2 * P(0 ≤Z ≤2)
= 1 - 2 * 0.4772
= 0.0456
[면적을 알고 있을 때 이에 대응하는 Z값을 찾는 법]
Q1. 평균(Z=0)에서 오른쪽으로 45% 해당하는 Z값은?
이럴 때는 표에서 0.45에 가장 가까운 값을 찾으면 된다.
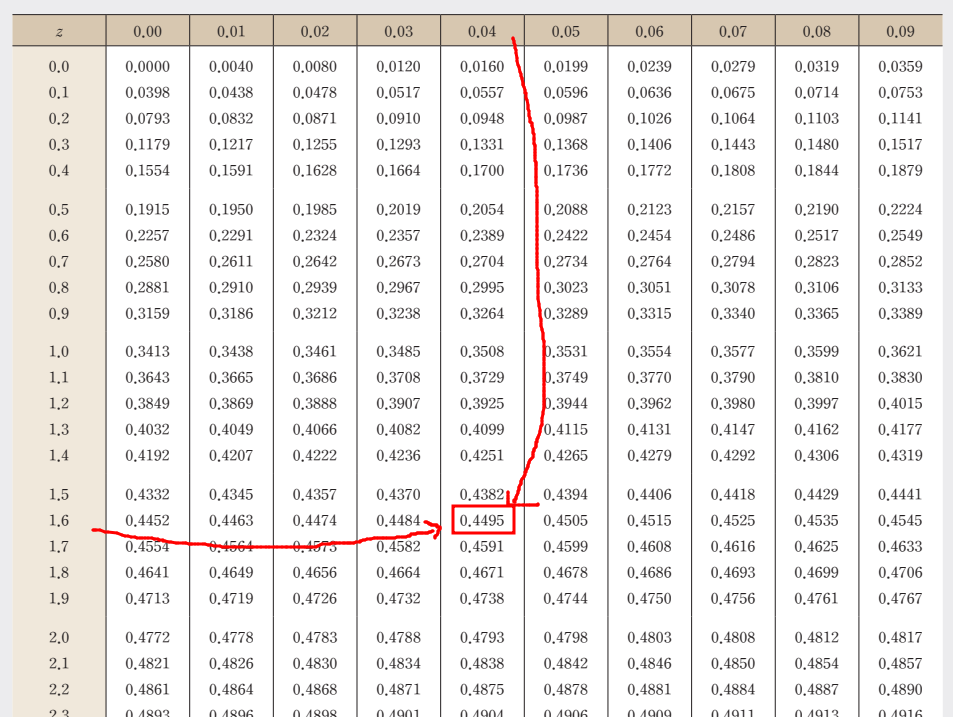
따라서, 값은 1.64
Q2. 평균에서 각각 30%에 해당하는 Z의 양쪽값은?
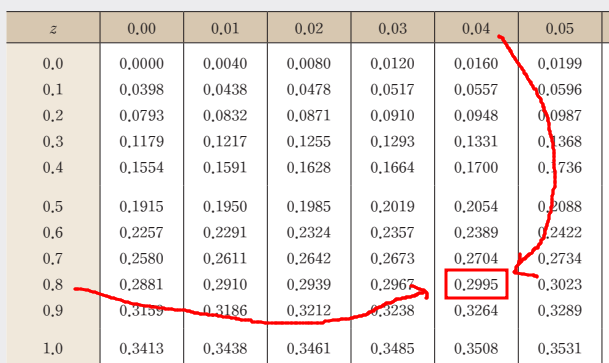
값은 ±0.84 (양쪽값이므로 ±)
정규분포의 확률계산 예제1 - 파이썬 코드 풀이
Q. 한 기업에서 신입사원을 대상으로 하는 인적성 검사를 실시한 결과 평균=100, 표준편차 =10이었다. 이 기업 신입사원들의 인적성 검사 점수분포가 정규분포를 이룬다고 가정할 때, 인적성 점수가 100에서 110 사이인 사원의 비율은?
# 정규분포
from scipy.stats import norm
# 평균과 표준편차 설정
mu = 100 # 평균
sigma = 10 # 표준편차
# CDF 계산
cdf_110 = norm.cdf(110, loc=mu, scale=sigma) # 110 이하일 확률
cdf_100 = norm.cdf(100, loc=mu, scale=sigma) # 100 이하일 확률
# 100에서 110 사이의 확률 계산
probability = cdf_110 - cdf_100
# 결과 출력
print(f'인적성 점수가 100에서 110 사이인 사원의 비율: {probability:.4f}')
파이썬에서 정규분포 확률을 계산하려면 scipy 라이브러리의 scipy.stats.norm 모듈을 사용하는 것이 일반적이다.
- PDF (Probability Density Function): 특정 값에서의 확률밀도를 계산.
scipy.stats.norm.pdf(x, loc=평균, scale=표준편차)
- CDF (Cumulative Distribution Function): 특정 값 이하의 확률을 계산.
scipy.stats.norm.cdf(x, loc=평균, scale=표준편차)
2. 그렇다면, 인적성 점수가 120 이상인 사원의 비율은?
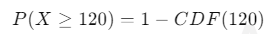
앞서 구한 100점과 110점의 CDF 를 구하듯이, 120점에 대한 확률을 구한 뒤 이를 1에서 빼면 된다.
from scipy.stats import norm
# 평균과 표준편차 설정
mu = 100 # 평균
sigma = 10 # 표준편차
# 120 이하일 확률 계산
cdf_120 = norm.cdf(120, loc=mu, scale=sigma)
# 120 이상일 확률 계산
probability = 1 - cdf_120
# 결과 출력
print(f'인적성 검사 점수가 120점 이상일 확률: {probability:.4f}')
두 답변을 합치면,
100에서 110 사이인 사원 비율: 34.13% (0.3413)
120점 이상인 사원 비율: 2.28% (0.0228)
정규분포의 확률계산 예제2 - 파이썬 코드 풀이
Q. 파이초등학교 학생들의 평균 키가 145cm 이고, 표준편차는 20cm 라고 한다. 학생들의 키의 분포가 정규분포를 이룬다고 하면 전체 학생 중에서 키가 120~135cm 인 학생의 비율은?
# 파이 초등학교 키에 따른 비율
from scipy.stats import norm
# 평균과 표준편차 설정
mu = 145 # 평균
sigma = 20 # 표준편차
# CDF 계산
cdf_120 = norm.cdf(120, loc=mu, scale=sigma) # 120 이하일 확률
cdf_135 = norm.cdf(135, loc=mu, scale=sigma) # 135 이하일 확률
# 120에서 135 사이의 확률 계산
probability = cdf_135 - cdf_120
# 출력
print(f'키가 120에서 135 사이인 학생의 비율: {probability:.4f}')
정규분포의 확률계산 예제3- 파이썬 코드 풀이
Q. 규포중학교의 중간고사 시험점수가 정규분포를 이루고 있고, 평균이 60점이며 표준편차는 15점이라고 한다. 이 학교에서 상위 10%에 해당하는 사람에게 장학금을 주려고 하는데, 몇 점 이상의 학생에게 지급하여야 하는가?
▶
정규분포에서 상위 10%에 해당하는 점수를 찾는 문제이다. 이를 위해 역누적분포함수(Percent Point Function, PPF)를 사용하면 되며, scipy.stats.norm.ppf 함수는 누적 확률을 기준으로 해당하는 점수를 구할 수 있다.
- 상위 10%에 해당하는 사람들은 누적 확률이 90% 이상인 학생들이다. 따라서 누적확률 0.9에 해당하는 점수를 찾아야 한한다.
- 평균이 60점, 표준편차가 15점인 정규분포에서 누적확률 0.9에 해당하는 점수를 계산한다
# 장학금 주기 위한 점수 기준
from scipy.stats import norm
# 평균과 표준편차 설정
mu = 60 # 평균
sigma = 15 # 표준편차
# ppf 계산
ppf = norm.ppf(0.9, loc=mu, scale=sigma) # 상위 10% (=누적 90%)
print('장학금을 받기 위한 점수 기준:{:.1f}'.format(ppf))
다음 내용
[파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.7)-2
puppy-foot-it.tistory.com
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.8)-1 (2) | 2024.10.11 |
|---|---|
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.7)-2 (3) | 2024.10.11 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.6)-2 (0) | 2024.10.11 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.6)-1 (5) | 2024.10.10 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.5) (2) | 2024.10.10 |



