이전 내용
[머신러닝] 모델 훈련 - 1
머신러닝 모델 훈련 머신러닝 모델이 어떻게 작동하는지 잘 이해하고 있으면 적절한 모델, 올바른 훈련 알고리즘, 작업에 맞는 좋은 하이퍼 파라미터를 빠르게 찾을 수 있다. 또한 디버깅이나
puppy-foot-it.tistory.com
학습 곡선
학습 곡선은 모델의 훈련 오차와 검증 오차를 훈련 반복 횟수의 함수로 나타낸 그래프이다.
고차 다항 회귀를 적용하면 일반 선형 회귀에서보다 훨씬 더 훈련 데이터에 잘 맞추려 할 것이다,
아래의 코드는 300차 다항 회귀 모델을 훈련 데이터에 적용하여 단순한 선형 모델이나 2차 다항 회귀 모델과 결과를 비교해본 것이다.
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
plt.figure(figsize=(6, 4))
for style, width, degree in (("r-+", 2, 1), ("b--", 2, 2), ("g-", 1, 300)):
polybig_features = PolynomialFeatures(degree=degree, include_bias=False)
std_scaler = StandardScaler()
lin_reg = LinearRegression()
polynomial_regression = make_pipeline(polybig_features, std_scaler, lin_reg)
polynomial_regression.fit(X, y)
y_newbig = polynomial_regression.predict(X_new)
label = f"{degree} degree{'s' if degree > 1 else ''}"
plt.plot(X_new, y_newbig, style, label=label, linewidth=width)
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([-3, 3, 0, 10])
plt.grid()
plt.show()
훈련하는 동안 훈련 세트와 검증 세트에서 일정한 간격으로 모델을 평가하고 그 결과를 그래프로 그리면 되는데, 모델을 점진적으로 훈련할 수 없는 경우 훈련 세트의 크기를 점점 늘려가면서 여러 번 훈련해야 한다.
사이킷런에는 이를 위해 교차 검증을 사용하여 모델을 훈련하고 평가하는 learning_curve() 함수가 있다.
- 이 함수는 훈련 세트의 크기를 증가시키면서 모델을 재훈련하지만, 모델이 점진적 학습을 지원하는 경우 learning_curve()를 호출할 때 exploit_incremental_learning=True 로 지정하면 대신 모델을 점진적으로 훈련시킨다.
- 이 함수는 모델을 평가한 훈련 세트 크기를 반환한다
- 이 함수는 각각의 크기와 교차 검증 폴드에서 측정한 훈련 및 검증 점수를 반환한다
from sklearn.model_selection import learning_curve
from sklearn.linear_model import LinearRegression
train_sizes, train_scores, valid_scores = learning_curve(
LinearRegression(), X, y, train_sizes=np.linspace(0.01, 1.0, 40), cv=5,
scoring='neg_root_mean_squared_error')
train_errors = -train_scores.mean(axis=1)
valid_errors = -valid_scores.mean(axis=1)
plt.plot(train_sizes, train_errors, 'r-+', linewidth=2, label='Train Set')
plt.plot(train_sizes, valid_errors, 'b-', linewidth=3, label='Valid Set')
plt.xlabel("Training set size")
plt.ylabel("RMSE")
plt.grid()
plt.legend(loc="upper right")
plt.axis([0, 80, 0, 2.5])
plt.show()
▶ 위의 학습 곡선은 두 곡선이 수평한 구간을 만들고 꽤 높은 오차에서 매우 가까이 근접해 있는 과소적합 모델의 전형적인 모습이다. 이러한 경우에는 훈련 샘플을 더 추가해도 효과가 없기 때문에 더 복잡한 모델을 사용하거나 더 나은 특성을 선택해야 한다.
[훈련 오차]
- 훈련 세트에 하나 혹은 두 개의 샘플이 있을 땐 모델이 완벽하게 작동
- 훈련 세트에 샘플이 추가됨에 따라 모델이 훈련 데이터를 완벽히 학습하는 것이 불가능해짐 (잡음, 비선형)
- 곡선이 어느 정도 평편해질 때까지 오차 계속 상승
[검증 오차]
- 초기에는 모델이 적은 수의 훈련 샘플로 훈련될 때는 제대로 일반화될 수 없어 검증 오차가 큼
- 모델에 훈련 샘플이 추가되며 학습이 되고 검증 오차 감소
- 데이터를 제대로 모델링할 수 없으므로 오차가 완만하게 감소하면서 훈련 세트의 그래프와 가까워짐
같은 데이터로 10차 다항 회귀 모델의 학습 곡선 그려보기
from sklearn.pipeline import make_pipeline
polynomial_regression = make_pipeline(
PolynomialFeatures(degree=10, include_bias=False),
LinearRegression())
train_sizes, train_scores, valid_scores = learning_curve(
polynomial_regression, X, y, train_sizes=np.linspace(0.01, 1.0, 40), cv=5,
scoring='neg_root_mean_squared_error')
train_errors = -train_scores.mean(axis=1)
valid_errors = -valid_scores.mean(axis=1)
plt.plot(train_sizes, train_errors, 'r-+', linewidth=2, label='Train Set')
plt.plot(train_sizes, valid_errors, 'b-', linewidth=3, label='Valid Set')
plt.xlabel("Training set size")
plt.ylabel("RMSE")
plt.grid()
plt.legend(loc="upper right")
plt.axis([0, 80, 0, 2.5])
plt.show()
[10차 다항 회귀의 학습 곡선과 이전 학습 곡선과의 차이점]
- 훈련 데이터의 오차가 이전보다 훨씬 낮다
- 두 곡선 사이에 공간이 있다. 이는 검증 데이터에서보다 훈련 데이터에서 모델이 훨씬 더 나은 성능을 보인다는 뜻이며, 곧 과대적합 모델의 특징을 의미한다. 그러나 더 큰 훈련 새트를 사용하면 두 곡선이 점점 가까워진다
▶ 과대적합 모델을 개선하는 한 가지 방법은 검증 오차가 훈련 오차에 근접할 때까지 더 많은 훈련 데이터를 추가하는 것이다.
★ 편향/분산 트레이드오프
모델의 일반화 오차가 세 가지 다른 종류의 오차의 합으로 표현될 수 있다.
- 편향: 일반화 오차 중에서 편향은 잘못된 가정으로 인한 것이다. 편향이 큰 모델은 훈련 데이터에 과소 적합되기 쉽다.
편향의 예) 데이터가 실제로는 2차인데 선형으로 가정하는 경우
- 분산: 훈련 데이터에 있는 작은 변동에 모델이 과도하게 민감하기 때문에 나타난다. 자유도가 높은 모델이 높은 분산을 가지기 쉬워 훈련 데이터에 과대적합되는 경향이 있다.
- 줄일 수 없는 오차: 데이터 자체에 있는 잡음 때문에 발생한다. 이 오차를 줄일 수 있는 유일한 방법은 데이터에서 잡음을 제거하는 것이다.
잡음 제거의 예) 고장 난 센서 같은 데이터 소스를 고치거나 이상치를 감지해 제거
- 모델의 복잡도가 커지면, 분산이 늘어나고 편향은 줄어듦.
- 모델의 복잡도가 줄어들면, 편향이 커지고 분산이 작아짐.
<보다 자세한 내용>
[머신러닝] 회귀 - 다항 회귀와 과대(과소) 적합
이전 내용 [머신러닝] 회귀 - LinearRegression 클래스사이킷런 LinearRegression scikit-learn: machine learning in Python — scikit-learn 1.5.2 documentationComparing, validating and choosing parameters and models. Applications: Improve
puppy-foot-it.tistory.com
규제가 있는 선형 모델
과대적합을 줄이는 좋은 방법은 모델을 규제하는 것인데, 자유도를 줄이면 데이터에 과대적합되기 더 어려워지기 때문이다. 선형 회귀 모델에서는 보통 모델의 가중치를 제한함으로써 규제를 가한다.
[릿지 회귀]
릿지 회귀는 학습 알고리즘을 데이터에 맞추는 것 뿐만 아니라 모델의 가중치가 가능한 한 작게 유지되도록 한다. 규제항은 훈련하는 동안에만 비용 함수에 추가되며, 모델의 훈련이 끝나면 모델의 성능을 규제가 없는 MSE(또는 RMSE)로 평가한다.
사이킷런에서 정규 방정식을 사용한 릿지 회귀 적용의 예
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=0.1, solver='cholesky') # 루이솔레스키가 발견한 행렬 분해 사용
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
확률적 경사 하강법 사용의 예
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(penalty='l2', alpha=0.1 / m, tol=None,
max_iter=1000, eta0=0.01, random_state=42)
sgd_reg.fit(X, y.ravel()) # fit() 은 1차원 타깃을 기대하므로 y.rabel()로 씀
sgd_reg.predict([[1.5]])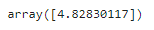
- penalty 매개변수는 사용할 규제 지정 (l2로 지정시 SGD가 MSE 비용 함수에 가중치 벡터의 l2 노름의 제곱에 alpha를 곱한 규제항이 추가됨.
- m으로 나누지 않는 것만 빼면 릿지 회귀와 같으므로, alpha=0.1/m 을 사용해 Ridge(alpha=0.1)과 같은 결과를 만듦.
※ RidgeCV 클래스도 릿지 회귀를 수행하지만 교차 검증을 사용하여 하이퍼파라미터를 자동으로 튜닝한다.
GridSearchCV를 사용하는 것과 거의 동일하지만 릿지 회귀에 최적화되어 있고 훨씬 더 빠르게 실행된다. 그 외 여러다른 추정기에도 LassoCV 및 ElasticNetCV와 같은 효율적인 CV 변형 모델이 있다. (주로 선형 모델)
[라쏘 회귀]
라쏘 회귀는 선형 회귀의 또 다른 규제 버전으로 릿지 회귀와는 달리 비용 함수에 가중치 벡터의 l1 노름을 사용한다.
라쏘 회귀의 중요한 특징은 덜 중요한 특성의 가중치를 제거하려고 한다는 점인데, 라쏘 회귀는 자동으로 특성 선택을 수행하고 희소 모델을 만든다.
Lasso 클래스를 사용한 간단한 사이킷런 예제
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
Lasso 대신 SGDRegressor을 사용할 수도 있다.
sgd_reg = SGDRegressor(penalty='l1', alpha=0.1, tol=None,
max_iter=1000, eta0=0.01, random_state=42)
sgd_reg.fit(X, y.ravel()) # fit() 은 1차원 타깃을 기대하므로 y.rabel()로 씀
sgd_reg.predict([[1.5]])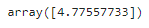
[엘라스틱넷]
엘라스틱넷 회귀는 릿지 회귀와 라쏘 회귀를 절충한 모델이며, 규제항은 릿지와 회귀의 규제항을 단순히 더한 것이며, 혼합 정도는 혼합 비율 r을 사용해 조절한다.
- r = 0: 엘라스틱넷은 릿지 회귀와 같다
- r = 1: 엘라스틱넷은 라쏘 회귀와 같다
사이킷런의 ElasticNet을 사용한 간단한 예제
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])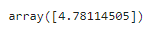
★ 엘라스틱넷 회귀, 릿지 회귀, 라쏘 횟쉬, 규제가 없는 일반적인 선형 회귀를 사용해야 하는 때
- 규제가 약간 있는 것이 대부분의 경우에 좋으므로 규제가 없는 일반적인 선형 회귀는 피하는 게 좋다
- 릿지가 기본이나, 몇 가지 특성만 유용하다고 생각되면 라쏘나 엘라스틱넷이 낫다
- 특성 수가 훈련 샘플 수보다 많거나 특성 몇 개가 강하게 연관되어 있을 때는 보통 라쏘가 문제를 일으키므로 엘라스틱넷이 좋다
[릿지 회귀, 라쏘 회귀, 엘라스틱넷에 대한 보다 자세한 개념은]
[머신러닝] 회귀 - 규제 선형 모델: 릿지, 라쏘, 엘라스틱넷
이전 내용 [머신러닝] 회귀 - 다항 회귀와 과대(과소) 적합이전 내용 [머신러닝] 회귀 - LinearRegression 클래스사이킷런 LinearRegression scikit-learn: machine learning in Python — scikit-learn 1.5.2 documentationCo
puppy-foot-it.tistory.com
[조기 종료]
검증 오차가 최솟값에 도달하면 바로 훈련을 중지시키는 것을 말하며 경사 하강법 같은 반복적인 학습 알고리즘을 규제하는 방식이다. 이 규제 기법은 매우 효과적이고 간단하다.
확률적 경사 하강법이나 미니배치 경사 하강법에서는 곡선이 그리 매끄럽지 않아 최솟값에 도달했는지 확인하기 어려울 수 있는데, 이럴 때는 검증 오차가 일정 시간 동안 최솟값보다 클 때(모델이 더 나아지지 않는다고 확신이 들 때) 학습을 멈추고 검증 오차가 최소였을 때의 모델 파라미터로 되돌리는 것이다.
from copy import deepcopy
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
import warnings
warnings.filterwarnings('ignore')
# 이전과 동일한 2차방정식 데이터셋을 생성하고 분할.
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1)
X_train, y_train = X[: m // 2], y[: m // 2, 0]
X_valid, y_valid = X[m // 2 :], y[m // 2 :, 0]
preprocessing = make_pipeline(PolynomialFeatures(degree=90, include_bias=False),
StandardScaler())
X_train_prep = preprocessing.fit_transform(X_train)
X_valid_prep = preprocessing.transform(X_valid)
sgd_reg = SGDRegressor(penalty=None, eta0=0.002, random_state=42)
n_epochs = 500
best_valid_rmse = float('inf')
train_errors, val_errors = [], [] #아래 그림을 위한 코드.
for epoch in range(n_epochs):
sgd_reg.partial_fit(X_train_prep, y_train)
y_valid_predict = sgd_reg.predict(X_valid_prep)
val_error = mean_squared_error(y_valid, y_valid_predict, squared=False)
if val_error < best_valid_rmse:
best_valid_rmse = val_error
best_model = deepcopy(sgd_reg)
# 훈련 오차를 평가하여 그림에 저장.
y_train_predict = sgd_reg.predict(X_train_prep)
train_error = mean_squared_error(y_train, y_train_predict, squared=False)
val_errors.append(val_error)
train_errors.append(train_error)
# 그림 생성.
best_epoch = np.argmin(val_errors)
plt.figure(figsize=(6, 4))
plt.annotate('Best model',
xy=(best_epoch, best_valid_rmse),
xytext=(best_epoch, best_valid_rmse + 0.5),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.05))
plt.plot([0, n_epochs], [best_valid_rmse, best_valid_rmse], "k:", linewidth=2)
plt.plot(val_errors, "b-", linewidth=3, label="Validation set")
plt.plot(best_epoch, best_valid_rmse, "bo")
plt.plot(train_errors, "r--", linewidth=2, label="Training set")
plt.legend(loc="upper right")
plt.xlabel("Epoch")
plt.ylabel("RMSE")
plt.axis([0, n_epochs, 0, 3.5])
plt.grid()
plt.show()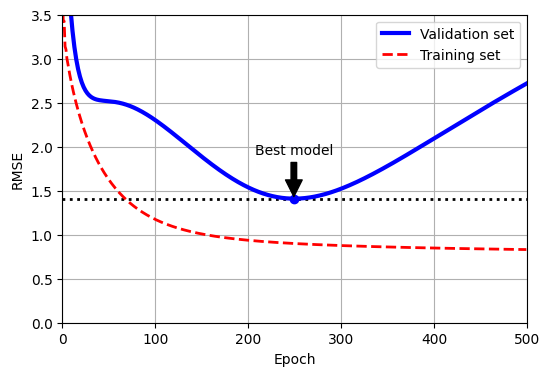
<코드 설명>
이 코드는 먼저 다항 특성을 추가하고 훈련 세트와 검증 세트 모두에 대해 모든 입력 특성의 스케일을 조정한다. 그런 다음 규제가 없고 학습률이 작은 SGDRegressor 모델을 생성한다.
훈련 반복에서는 fit() 대신 partial_fit()을 호출하여 점진적인 학습을 수행하고 각 에포크에서 검증 세트의 RMSE를 측정해 지금까지 확인된 가장 낮은 RMSE 보다 낮으면 best_model 변수에 모델의 복사본을 저장한다.
이 구현은 실제로 학습을 중지시키지는 않지만 학습 후 최상의 모델로 되돌릴 수 있다. 또한, copy.deepcopy()를 사용하여 모델을 복사하는데, 이 함수는 모델의 하이퍼파라미터와 학습된 파라미터를 모두 복사한다.
(sklearn.base.clone() 은 모델의 하이퍼파라미터만 복사)
1. 필요한 라이브러리 설정
- copy 모듈의 deepcopy는 객체의 깊은 복사용.
- sklearn.metrics의 mean_squared_error는 모델의 오류 측정을 위해 사용.
- sklearn.preprocessing의 StandardScaler는 데이터 표준화를 위해 사용
2. 데이터셋 생성 및 분할
- 데이터 생성: 난수 생성기는 일관되게 하기 위해 np.random.seed(42)로 설정.
- X는 -3에서 3 사이의 값들로 이루어진 100개의 샘플을 가지며, y는 2차 방정식을 기반으로 생성된 타겟 값.
- 데이터는 X_train, y_train (훈련 데이터)와 X_valid, y_valid (검증 데이터)로 분할.
3. 데이터 전처리
- PolynomialFeatures는 변수의 다항 특성을 생성하며, degree=90은 최대 차수를 90으로 설정.
- StandardScaler는 각 특성을 표준화하여 평균을 0, 분산을 1로 만듦.
- make_pipeline을 사용해 전처리 파이프라인을 생성하고, 이를 훈련 및 검증 데이터에 적용.
4. 모델 학습 및 평가
- SGDRegressor는 확률적 경사 하강법으로 선형 모델을 학습하며, 여기서는 규제가 없는(penalty=None) 형태로 사용되며 학습률은 eta0=0.002로 설정.
- n_epochs는 학습 반복 횟수를 나타내며, 500으로 설정.
- 모델은 각 에포크 동안 partial_fit을 통해 훈련.
- 검증 데이터로 예측한 결과와 실제 값을 이용해 val_error를 계산하고, 이를 통해 최적 모델(best_model)을 저장.
- 마찬가지로 훈련 데이터에 대한 예측 결과로 train_error를 계산하고 오류 리스트에 저장.
5. 결과 시각화
- best_epoch는 검증 오류가 최소인 에포크를 찾음.
- 그래프를 생성하여 훈련 및 검증 데이터의 RMSE를 시각화하며, 최적 모델의 위치를 강조.
로지스틱 회귀
로지스틱 회귀는 샘플이 특정 클래스에 속할 확률을 추정하는 데 널리 사용된다.
[머신러닝] 로지스틱 회귀
이전 내용 [머신러닝] 회귀 - 규제 선형 모델: 릿지, 라쏘, 엘라스틱넷이전 내용 [머신러닝] 회귀 - 다항 회귀와 과대(과소) 적합이전 내용 [머신러닝] 회귀 - LinearRegression 클래스사이킷런 LinearReg
puppy-foot-it.tistory.com
◆ 확률 추정
선형 회귀 모델과 같이 로지스틱 회귀 모델은 입력 특성의 가중치 합을 계산하고 편향을 더한다. 대신 선형 회귀처럼 바로 결과를 출력하지 않고 결괏값의 로지스틱을 출력한다.
로지스틱은 0과 1 사이의 값을 출력하는 시그모이드 함수(S자 형태)이다.
◆ 훈련과 비용 함수
로지스틱 회귀 모델의 훈련을 시키는 목적은 양성 샘플에 대해서는 높은 확률을 추정하고 음성 샘플에 대해서는 낮은 확률을 추정하는 모델의 파라미터 벡터를 찾는 것이다.
이 비용 함수는 t가 0에 가까워지면 -log(t) 가 매우 커지므로 타당하고 볼 수 있다. 그러므로
- 모델이 양성 샘플을 0에 가까운 확률로 추정하면 비용이 크게 증가
- 음성 샘플을 1에 가까운 확률로 추정해도 비용이 크게 증가
- t가 1에 가까우면 -log(t)는 0에 가까워지면서 기대한 대로 음성 샘플의 확률을 0에 가깝게 추정하거나 양성 샘플의 확률을 1에 가깝게 추정하면 비용은 0에 가까워짐.
※ 로그 손실(log loss): 모든 훈련 샘플의 비용을 평균한 것. (전체 훈련 세트에 대한 비용 함수)
이 비용 함수는 볼록 함수이므로 경사 하강법이 전역 최솟값을 찾는 것을 보장한다. 모든 편도함수를 포함한 그레이디언트 벡터를 만들면 배치 경사 하강법 알고리즘을 만들 수 있다.
◆ 결정 경계
붓꽃(iris) 데이터셋을 사용하여 꽃잎의 너비를 기반으로 Iris-Versicolor 종을 감지하는 분류기 만들기
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# 데이터 로드
iris = load_iris(as_frame=True)
# 데이터 분할
X = iris.data[['petal width (cm)']].values
y = iris.target_names[iris.target] =='virginica'
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
# 훈련 세트에서 로지스틱 회귀 모델 훈련
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_train, y_train)
# 꽃잎의 너비가 0~3cm 인 꽃에 대해 모델의 추정 확률 계산
X_new = np.linspace(0, 3, 1000).reshape(-1, 1) # 열 벡터로 바꿈
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] > 0.5][0,0]# 시각화
plt.plot(X_new, y_proba[:,0], 'b--', linewidth=2,
label="Not Iris virginica proba")
plt.plot(X_new, y_proba[:, 1], 'g-', linewidth=2, label='Iris-Virginica proba')
plt.plot([decision_boundary, decision_boundary], [0,1], 'k', linewidth=2,
label='Dicision Boundary')
plt.arrow(x=decision_boundary, y=0.08, dx=-0.3, dy=0,
head_width=0.05, head_length=0.1, fc="b", ec="b")
plt.arrow(x=decision_boundary, y=0.92, dx=0.3, dy=0,
head_width=0.05, head_length=0.1, fc="g", ec="g")
plt.plot(X_train[y_train == 0], y_train[y_train == 0], "bs")
plt.plot(X_train[y_train == 1], y_train[y_train == 1], "g^")
plt.xlabel("Petal width (cm)")
plt.ylabel("Probability")
plt.legend(loc="center left")
plt.axis([0, 3, -0.02, 1.02])
plt.grid()
plt.show()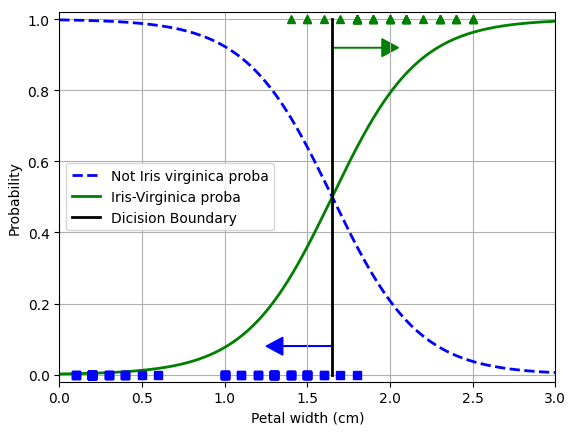
Iris-Virginica (삼각형) 꽃잎 너비는 1.4~2.5cm에 분포하며, 다른 붓꽃(사격형)은 일반적으로 꽃잎 너비가 더 작아 0,1~1.8cm에 분포한다. 꽃잎 너비가 2.0cm 이상인 꽃은 분류기가 Iris-Virginica라고 강하게 확신하며 1cm 미만이면 Iris-Virginica가 아니라고 강하게 확신한다.
print('결정 경계:', decision_boundary)
클래스를 예측하려고 하면 가장 가능성이 높은 클래스를 반환하는데, 양쪽의 확률이 똑같이 50%가 되는 1.65cm 근방에서 결정 경계가 만들어지고 꽃잎 너비가 1.6cm보다 크면 분류기는 Iris-Virginica로 분류하고, 그보다 작으면 아니라고 예측할 것이다.
log_reg.predict([[1.7], [1.5]])
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = iris.target_names[iris.target] == 'virginica'
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
log_reg = LogisticRegression(C=2, random_state=42)
log_reg.fit(X_train, y_train)
# 등고선 그래프
x0, x1 = np.meshgrid(np.linspace(2.9, 7, 500).reshape(-1, 1),
np.linspace(0.8, 2.7, 200).reshape(-1, 1))
X_new = np.c_[x0.ravel(), x1.ravel()] # 그림의 포인트당 하나의 샘플
y_proba = log_reg.predict_proba(X_new)
zz = y_proba[:, 1].reshape(x0.shape)
# 결정 경계
left_right = np.array([2.9, 7])
boundary = -((log_reg.coef_[0, 0] * left_right + log_reg.intercept_[0])
/ log_reg.coef_[0, 1])
plt.figure(figsize=(10, 4))
plt.plot(X_train[y_train == 0, 0], X_train[y_train == 0, 1], "bs")
plt.plot(X_train[y_train == 1, 0], X_train[y_train == 1, 1], "g^")
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)
plt.clabel(contour, inline=1)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.27, "Not Iris virginica", color="b", ha="center")
plt.text(6.5, 2.3, "Iris virginica", color="g", ha="center")
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.axis([2.9, 7, 0.8, 2.7])
plt.grid()
plt.show()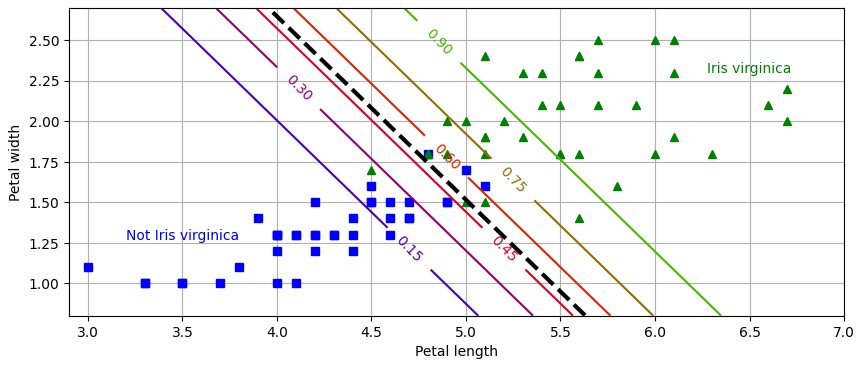
훈련이 끝나면 로지스틱 회귀 분류기가 꽃잎 너비와 꽃잎 길이라는 두 개의 특성을 기반으로 새로운 꽃이 Iris-Virginica 인지 확률을 추정할 수 있으며, 점선은 모델이 50% 확률을 추정하는 지점으로 이 모델의 결정 경계이다.
15%부터 90%까지 나란한 직선들은 모델이 특정 확률을 출력하는 포인트를 나타내고, 모델은 맨 오른쪽 위의 직선을 넘는 꽃들을 90% Iris-Virginica 라고 판단할 것이다.
다른 선형 모델처럼 로지스틱 회귀 모델도 l1, l2 페널티를 사용하여 규제할 수 있으며, 사이킷런은 l2 페널티를 기본으로 한다.
[소프트맥스 회귀]
로지스틱 회귀 모델은 여러 개의 이진 분류기를 훈련시켜 연결하지 않고 직접 다중 클래스를 지원하도록 일반화될 수 있는데, 이를 소프트맥스 회귀 또는 다항 로지스틱 회귀라고 한다.
샘플 x가 주어지면 먼저 소프트맥스 회귀 모델이 각 클래스 k에 대한 점수를 계산하고, 그 점수에 소프트맥스 함수 (또는 정규화된 지수 함수)를 적용하여 각 클래스의 확률을 추정한다.
각 클래스는 자신만의 파라미터 벡터가 있으며, 이 벡터들은 파라미터 행렬에 행으로 저장된다.
샘플x에 대해 각 클래스의 점수가 계산되면 소프트맥스 함수를 통과시켜 클래스 k에 속할 확률을 추정할 수 있다. 이 함수는 각 점수에 지수 함수를적용한 후 정규화(모든 지수 함수 결과의 합으로 나눔)하며, 일반적으로 이 점수를 로짓 또는 로그-오즈 라고 한다.
로지스틱 회귀 분류기와 마찬가지로 기본적으로 소프트맥스 회귀 분류기는 추정 확률이 가장 높은 클래스(가장 점수가 높은 클래스)를 선택하며, argmax 연산은 함수를 최대화하는 변수의 값을 반환한다.
소프트맥스 회귀 분류기는 한 번에 하나의 클래스만 예측하므로, (다중 출력이 아님) 종류가 다른 상호 배타적인 클래스에서만 사용해야 한다. 예를 들어 붗꽃 에서는 사용할 수 있으나, 하나의 사진에서 여러 사람의 얼굴을 인식하는 데는 사용할 수 없다.
소프트맥스 회귀는 모델이 타깃 클래스에 대해서는 높은 확률을, 다른 클래스에 대해서는 낮은 확률을 추정하도록 만드는 것이 목적이다. 크로스 엔트로피 비용 함수를 최소화하는 것은 타깃 클래스에 대해 낮은 확률을 예측하는 모델을 억제하므로 이 목적에 부합한다.
※ 크로스 엔트로피: 추정된 클래스의 확률이 타깃 클래스에 얼마나 잘 맞는지 측정하는 용도로 종종 사용된다.
사이킷런의 LogisticRegression은 클래스가 둘 이상일 때 자동으로 소프트맥스 회귀를 사용하며, multi_class 매개변수를 'multinomial'로 바꾸면 소프트맥스 회귀를 사용할 수 있다. 또한 소프트맥스 회귀를 사용하려면 solver 매개변수에 'lbfgs'와 같이 소프트맥스 회귀를 지원하는 알고리즘을 지정해야 한다.
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = iris['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
softmax_reg = LogisticRegression(C=30, random_state=42)
softmax_reg.fit(X_train, y_train)
# 꽃잎의 길이가 5cm, 너비가 2cm인 붓꽃을 발견했다고 가정
softmax_reg.predict([[5, 2]])
softmax_reg.predict_proba([[5, 2]]).round(2)
iris.target_names
▶ 꽃잎의 길이가 5cm, 너비가 2cm인 붓꽃을 발견했다고 가정하고 모델에 품종 구분을 질의하면 96%의 확률로 클래스 2에 해당하는 Iris-Virginica 출력
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(["#fafab0", "#9898ff", "#a0faa0"])
x0, x1 = np.meshgrid(np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1))
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)
zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y == 2, 0], X[y == 2, 1], "g^", label="Iris virginica")
plt.plot(X[y == 1, 0], X[y == 1, 1], "bs", label="Iris versicolor")
plt.plot(X[y == 0, 0], X[y == 0, 1], "yo", label="Iris setosa")
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap="hot")
plt.clabel(contour, inline=1)
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.legend(loc="center left")
plt.axis([0.5, 7, 0, 3.5])
plt.grid()
plt.show()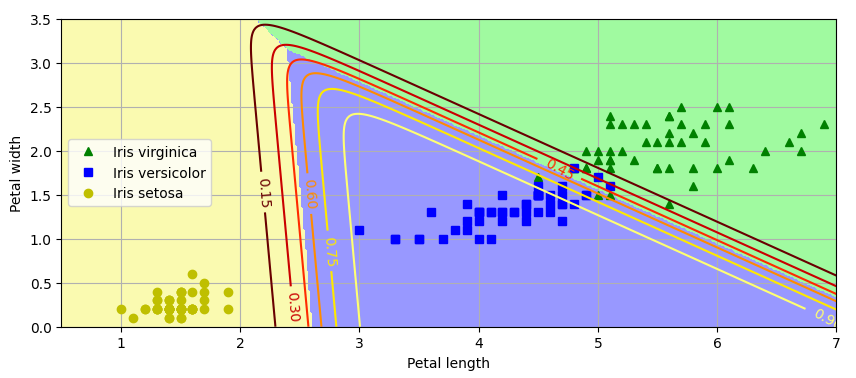
위의 그림은 만들어진 결정 경계를 배경색으로 구분하여 나타내고 있으며, Iris-Versicolor 클래스에 대한 확률을 곡선으로 나타냈다.
다음 내용
[머신러닝] 서포트 벡터 머신(SVM)
머신러닝 기반 분석 모형 선정 [머신러닝] 머신러닝 기반 분석 모형 선정머신러닝 기반 분석 모형 선정 지도 학습, 비지도 학습, 강화 학습, 준지도 학습, 전이 학습 1) 지도 학습: 정답인 레
puppy-foot-it.tistory.com
[출처]
핸즈 온 머신러닝
'[파이썬 Projects] > <파이썬 머신러닝>' 카테고리의 다른 글
| [머신러닝] 결정 트리 (추가) (1) | 2024.11.14 |
|---|---|
| [머신러닝] 서포트 벡터 머신(SVM) (1) | 2024.11.14 |
| [머신러닝] 모델 훈련 - 1 (6) | 2024.11.09 |
| [머신러닝] 분류: MNIST 데이터셋 실습 - 2 (0) | 2024.11.09 |
| [머신러닝] 분류: MNIST 데이터셋 실습 - 1 (0) | 2024.11.09 |



