★ K-Fold에 대한 설명으로 옳지 않은 것은?
1. 데이터를 K개로 나눈다.
2. 1개는 훈련 데이터, (K-1)개는 검증 데이터로 사용 ▶ 1개는 평가 데이터, (K-1) 개는 훈련 데이터
3. K번 반복 수행
4. 결과를 K에 다수결 또는 평균으로 분석
▶ K-Fold Cross Validation: 데이터 집합을 무작위로 동일 크기를 갖는 부분 집합으로 나누고, 그중 1개 집합을 평가 데이터로 (Test SET), 나머지 (K-1) 개 집합을 훈련 데이터 (Training Set)로 선정하여 분석 모형을 평가하는 기법.
모든 데이터를 훈련과 평가에 사용할 수 있으며, K번 반복 수행하며, K값이 증가하면 수행 시간과 계산량도 많아짐.
★ 다음 중 비복원 추출을 이용한 교차 검증 방법은?
1. Bootstrap
2. Holdout Cross Validation
3. K-Fold Cross Validation
4. Leave-One-Out Cross Validation
▶ Holdout Cross Validation: 전체 데이터를 비복원 추출 방법을 이용하여 랜덤하게 훈련 데이터와 평가 데이터로 나눠 검증하는 기법
★ 다음 중 주어진 자료에서 단순 랜덤 복원추출 방법을 활용하여 동일한 크기의 표본을 여러 개 생성하는 샘플링 방법은?
1. 모수 유의성 검정
2. 부트스트랩
3. 랜덤 샘플링
4. 홀드 아웃 교차 검증
★ 10개의 샘플 데이터를 LpOCV (Leave-p-Out Cross Validation)틀 통하여 교차 검증을 실시할 때, p=2일 경우에는 반복되는 교차 검증은 몇 번인가?
1. 20
2. 80
3. 45
4. 90
▶ n개의 데이터에서 LpOCV를 사용할 때 반복되는 교차 검증의 횟수는 nCp.
nCp= 10! / (10-2)! * 2! = 10! / 8! * 2! = 10 * 9 / 2 * 1 = 45
◎LpOCV : LOOCV에서 1개의 샘플이 아닌 p개의 샘플을 테스트에 사용하는 교차 검증 기법 (게산 시간에 대한 부담이 매우 큼)
◎ LOOCV: 전체 데이터 N개에서 1개의 샘플만을 평가 데이터에 사용하고 나머지 (N-1)개는 훈련 데이터로 사용하는 과정을 N번 반복하는 교차 검증 기법 (많은 데이터를 훈련에 사용할 수 있으나, 수행 시간과 계산량이 많다.)
★ 다음은 혼동행렬 (Confusion Matrix) 이다. 민감도 (Sensitive)와 정밀도 (Precision) 는?
| 실제 (Actual) | |||
| 참 | 거짓 | ||
| 예측 (Predict) | 참 | 4 | 2 |
| 거짓 | 1 | 3 | |
민감도: 4/5, 정밀도: 2/3
▶ 민감도의 계산식: TP/TP+FN = 4/4+1 = 4/5 | 정밀도의 계산식: TP/TP+FP = 4/4+2 = 2/3
★ 혼동행렬의 평가지표에서 실제로 '부정'인 범주 중에서 '부정'으로 올바르게 에측한 비율은?
1. 민감도 (Sensitive)
2. 특이도 (Specificity)
3. 지지도 (Support)
4. 유사도 (Similarity)
▶ 특이도는 실제로 '부정'인 범주 중에서 '부정'으로 올바르게 예측 (TN)한 비율
특이도의 계산식: TN/TN+FP
★ 다음은 암진단을 예측한 것과 실제 암 진단 결과를 혼동 행렬로 나타낸 것이다. 아래 표를 보고 TPR, FPR의 확률을 계산하시오.
| Actual | |||
| 0 | 1 | ||
| Predict | 0 | 45(TP) | 15(FP) |
| 1 | 5(FN) | 235(TN) | |
TPR: 9/10, FPR: 3/50
▶ TPR = TP/TP+FN = 45/45+5 = 45/50 = 9/10 | FPR = FP/FP+TN = 15/15+235 = 15/250 = 3/50
★ y=0 혹은 y=1 값을 가지는 이진 분류 분석에서 민감도, 특이도가 둘 다 1일 때 정확도는?
1. 0
2. 1/2
3. 1
4. 알 수 없음
▶ 민감도가 1이라면 FN은 0이 되고, 특이도가 1이라면 FP는 0
정확도에서 FP와 FN이 0이 되면 TP+TN / TP +TN = 1
★ 혼동 행렬에서 FN이 의미하는 것은?
1. 실제 True, 예측 True
2. 실제 False, 예측 True
3. 실제 True, 예측 False
4. 실제 False, 예측 False
★ 재현율(Recall)이 60%, 정밀도 (Precision)가 40%일 때, F1-Score는?
48%
▶ F1-Score = 2* {(정밀도*재현율)/(정밀도+재현율)} = 2*{(0.6*0.4)/(0.6+0.4)} = 0.48/1 = 48%
★ 분석 모델에서 구한 분류의 예측 범주와 데이터의 실제 분류 범주를 교차 표 형태로 정리한 평가지표는?
▶ 혼동행렬
★ 아래에서 설명하고 있는 혼동 행렬을 통한 분류 모형의 평가지표는?
| - 참 긍정률 (TP Rate) 라고도 불리는 지표 - 실제로 '긍정'인 범주 중에서 '긍정'으로 올바르게 예측 (TP)한 비율 - Recall, Hit Ratio, TP Rate 로도 지칭 |
1. 정확도 (Accuracy) ▶ 실제 분류 범주를 정확히 예측한 비율
2. 정밀도 (Precision) ▶ '긍정'으로 예측한 비율 중에서 실제로 '긍정' (TP)인 비율
3. 특이도 (Specificity) ▶ 실제로 '부정'인 범주 중에서 '부정'으로 올바르게 예측 (TN)한 비율
4. 민감도 (Sensitive)
◎ 혼동행렬 (Confusion Matrix)
분석 모델에서 구한 분류의 예측 범주와 데이터의 실제 분류 범주를 교차 표 형태로 정리한 행렬
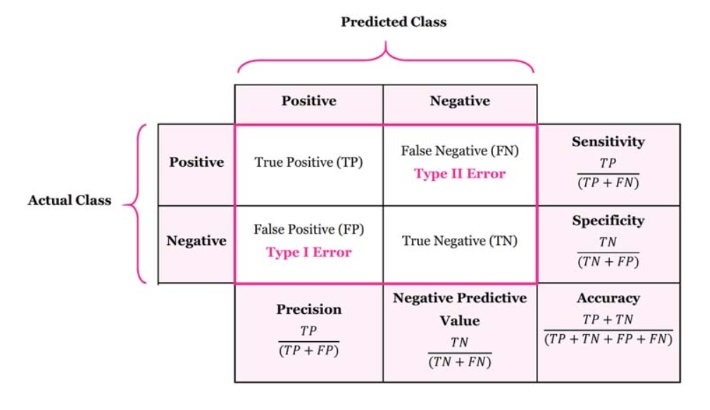
1) 작성 방법
| 예측이 정확한 경우 |
True Positive (TP) | 실제값, 예측값 모두 Positive |
| True Negative (TN) | 실제값, 예측값 모두 Negative | |
| 예측이 틀린 경우 |
False Positive (FP) | 실제값 Negative, 예측값 Positive |
| False Negative (FN) | 실제값 Positive, 예측값 Negative |
2) 평가지표
| 평가지표 | 계산식 | 설명 |
| 정확도 (Accuracy) | TP + TN / TP+TN+FP+FN | - 실제 분류 범주를 정확히 예측한 비율 - 전체 예측에서 참 긍정(TP)과 참 부정(TN)이 차지하는 비율 |
| 오차 비율 (Error Rate) |
FP + FN / TP+TN+FP+FN | - 실제 분류 범주를 잘못 분류한 비율 - 오차비율 = 1- (정확도) |
| 참 긍정률 = 재현률 = 민감도 (Sensitive) |
TP / TP + FN | - 실제로 '긍정'인 범주 중에서 '긍정'으로 올바르게 예측(TP)한 비율 |
| 특이도 (Specificity) | TN / TN+FP | - 실제로 '부정'인 범주 중에서 '부정'으로 올바르게 예측 (TN)한 비율 |
| 거짓 긍정률 (FP Rate) | FP / TN + FP | - 실제로 '부정'인 범주 중에서 '긍정' 으로 잘못 예측 (FP)한 비율 |
| 정밀도 (Precision) | TP / TP + FP | - '긍정'으로 예측한 비율 중에서 실제로 '긍정' (TP)인 비율 |
| F1 지표 (F1-Score) | 2 x {(정밀도 * 재현율) / (정밀도+ 재현율)} |
★ 다음 중 ROC 커브에 대한 설명으로 적합하지 않은 것은?
1. x축은 특이도를 의미한다.
2. y축은 민감도를 의미한다.
3. AUC (Area Under ROC) 1.0에 가까울수록 분석 모형 성능 우수
4. AUC (Area Under ROC) 0.5일 경우, 랜덤 선택에 가까운 성능
▶ x축은 특이도가 아닌 거짓 긍정률 (FP Rate)(=1-특이도)
y축은 참 긍정률 (TP Rate) = 재현율 (Recall) = 민감도 (Sensitive)
★ 다음 중 ROC 곡선에 대한 설명으로 올바르지 않은 것은?
1. ROC 곡선은 가로축(x)을 혼동 행렬의 거짓 긍정률로 두고 세로축(y)을 참 긍정률로 두어 시각화한 그래프
2. 거짓 긍정률(FPR) 은 특이도와 같음
3. AUC 는 ROC 곡선 아래의 면적으로, 면적을 모형의 평가지표로 삼는다
4. 참 긍정률(TPR) 은 민감도와 같음
▶ 거짓 긍정률은 1-특이도와 같음
★ ROC 곡선에 대한 설명으로 틀린 것은?
1. 민감도0, 특이도 1인 점을 지닌다
2. 민감도 1, 특이도 0인 점을 지닌다
3. 가장 이상적인 것은 민감도 1, 특이도 1일 때이다
4. ROC 곡선의 가로축의 값이 증가할수록 특이도 증가
▶ ROC 곡선은 가로축을 혼동 행렬의 거짓 긍정률로 두고 세로축을 참 긍정률로 두어 시각화한 그래프
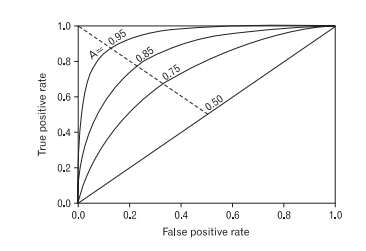
◎ ROC 커브 (곡선) (Receiver Operating Characteristic Curve)
- ROC 곡선은 가로축(x)을 혼동 행렬의 거짓 긍정률 (FP RATE)로 두고 세로축(y)을 참 긍정률 (TP Rate)로 두어 시각화한 그래프
- 그래프가 왼쪽 꼭대기에 가깝게 그려질수록 분류 성능 우수
- 거짓 긍정률과 참 긍정률은 어느 정도 비례 관계
- 진단의 정확도를 측정할 때 사용하며, ROC 곡선 아래의 면적을 모형의 평가지표로 삼는다
- AUC의 값은 항상 0.5~1의 값을 가지며, 1에 가까울수록 좋은 모형
★ 독립변수와 종속변수의 유형에 따른 분석방법으로 틀린 것은?
1. T-검정은 종속변수가 수치형이고 2개 범주의 독립변수를 사용하여 분석하는 방법이다
2. 로짓 모형은 종속변수가 범주형이고 독립변수가 수치형 또는 범주형일 경우 사용하는 분석 방법이다
3. X^2 검정(카이제곱 검정)은 독립변수와 종속변수가 모두 범주형일 경우 사용하는 분석 방법이다
4. 공분산 분석(ANCOVA)는 종속변수가 범주형, 독립변수가 연속형인 방법이다.
▶ 공분산 분석 (ANCOVA)은 분산 분석과 회귀 분석을 결합한 모형 (독립변수 - 범주형, 종속변수 - 연속형)
★ 다음 중 회귀 모형의 평가에 많이 사용되는 모형의 평가지표이며 오차 제곱합으로 계산되는 평가지표는?
1. AE ▶ 평균 오차 (Average Error)
2. SSE
3. MAE ▶ 평균 절대 오차 (Mean Absolute Error)
4. 결정계수 ▶ 회귀 모형이 실젯값을 얼마나 잘 나타내는지에 대한 비율
▶ SSE (Error Sum of Square): 예측값과 실젯값의 차이인 오차의 제곱 합으로 계산. (회귀 모형의 평가에 많이 사용)
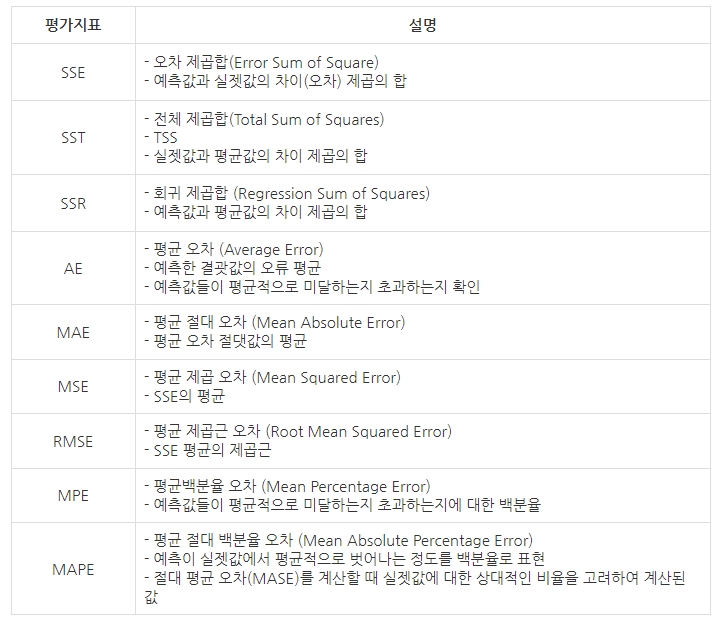
★ 다음 중 회귀모형의 기본 평가지표에 대한 설명 중 가장 올바르지 않은 것은?
1. SSE: 오차 제곱합. 예측값과 실제값의 차이 제곱의 합
2. SST: 전체 제곱합, 예측값과 평균값의 차이 제곱의 합
3. AE: 평균 오차. 에측한 결과값의 오류 평균
4. MAE: 평균 절대 오차. 실제값과 예측값 차이의 절대값에 대한 평균
▶ SST는 전체 제곱합 (실제값과 평균값의 차이 제곱의 합)
★ 다음 중 회귀 모형의 결정계수에 대한 설명으로 가장 올바르지 않은 것은?
1. 선형 회귀 분석의 성능 검증지표로 많이 이용 됨
2. 회귀 모형이 실제값을 얼마나 잘 나타내는지에 대한 비율
3. 결정계수가 1에 가까울수록 실제값을 잘 설명
4. 값의 범위는 -1 ≤ R^2 ≥ 1
▶값의 범위는 0 ≤ R^2 ≥ 1
★ 다음 중 수정된 결정계수에 대한 설명 중 가장 옳지 않은 것은?
1. 적절하지 않은 독립변수를 추가하는 것에 페널티를 부과한 결정계수
2. 모형에 유용한 변수들을 추가할수록 수정된 결정계수의 값은 감소
3. 수정된 결정계수는 항상 결정계수보다 작음
4. 독립변수의 개수가 다른 모형을 평가할 때 사용
▶ 수정된 결정계수는 모형에 유용한 변수들을 추가할수록 수정된 결정계수의 값 증가
★ 다음 중 Q-Q Plot에 대한 설명 중 가장 옳지 않은 것은?
1. Q-Q Plot은 그래프를 통하여 정규성 가정을 검정하는 방법
2. 대각선 참조선을 따라서 값들이 분포하게 되면 정규성 가정을 만족한다고 판단
3. 결과 해석이 객관적
4. 대각선 참조선을 따라서 값들이 한쪽으로 치우치는 모습이라면 정규성 가정에 위배되었다고 판단
▶Q-Q Plot은 한쪽으로 치우쳤다라고 판단하는 기준이 모호하므로 (주관적) 보조용으로 사용
★ 다음 중 데이터의 정규성을 확인하기 위한 방법으로 가장 올바르지 않은 것은?
1. 히스토그램
2. 샤피로-윌크 검정
3. 더빈-왓슨 테스트
4. Q-Q Plot
▶ 더빈-왓슨 테스트는 회귀 모형 오차항의 자기 상관이 있는지에 대한 검정
| 검정기법 | 샤피로-윌크 검정, 콜모고로프-스미르노프 적합성 검정 등 |
| 시각화 | 히스토그램, Q-Q Plot |
★ 다음 중 정규성 기법 중 Q-Q Plot에 대한 설명으로 올바르지 않은 것은?
1. 그래프를 이용하여 정규성 가정을 시각적으로 검정하는 방법
2. Q-Q Plot에서 대각선 참조선을 따라서 값들이 분포하게 되면 정규성 가정을 만족한다고 판단
3. 데이터가 어떤 특정한 분포를 따르는가를 비교할 때도 사용
4. 정규성 가정에 위배되었다는 판단 기준이 모호해서 Q-Q Plot은 보조용으로 사용하는 것을 권장
▶ 데이터가 어떤 특정한 분포를 따르는가를 비교할 때에는 콜모고로프-스미르노프 적합성 검정 (K-S 검정) 사용
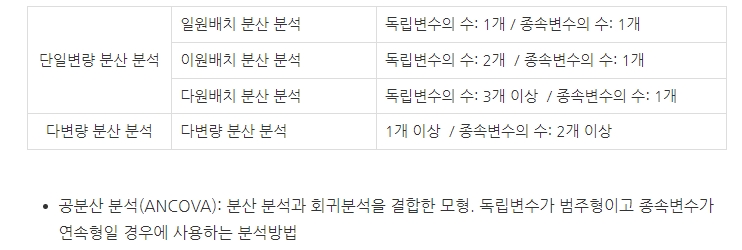
★ 다음 중 두 모집단 분산 간의 비율에 대한 검정으로 가장 옳은 것은?
1. F-검정 ▶ 두 표본의 분산에 대한 차이가 통계적으로 유의한가 판별
2. 일원 분산 분석
3. ANOVA
4. 이원 분산 분석
▶ 분산분석 (ANOVA): 두 개 이상의 집단 간 비교를 수행하고자 할 때 집단 내의 분산, 총 평균과 각 집단의 평균 차이에 의해 생긴 집단 간 분산 비교로 얻은 F-분포를 이용하여 가설검정 수행
★ 다음 중 귀무가설에서 검정 통계량의 분포를 정규분포로 근사할 수 있는 통계 검정은?
1. Z-검정
2. T-분포
3. 분산 분석
4. 카이제곱 검정
★ 다음 중에서 표본 집단의 분포가 주어진 특정 이론을 따르고 있는지를 검정하는 기법은?
1. 적합도 검정
2. F-검정
3. 모수 유의성 검정
4. T-검정
★ 다음 중 T-분포에 대한 설명으로 올바르지 않은 것은?
1. 적은 표본으로도 모집단 평균을 추정하려고 정규분포 대신에 사용되는 확률 분포
2. 자유도가 감소할수록 표준 정규분포에 가까워짐
3. 모집단이 정규분포라는 정도만 알고, 모분산을 모를 때 표본분산으로 대체하여 모평균을 구할 때 사용
4. 표준 정규분포와 유사하게 0을 중심으로 좌우대칭이나, 표준 정규분포보다 평평
▶ 자유도가 증가할수록 표준 정규분포에 가까워짐


★ 분석 변수 선택 기법 중 가중치의 제곱합을 추가하는 것은?
1. 릿지 (Ridge)
2. 라쏘 (Lasso) ▶ 기존 비용 함수에 모든 가중치 w들의 절댓값 합계 추가 (L1 규제)
3. 엘라스틱 넷 (Elastic Net) ▶ 기존 비용 함수에 L1 규제, L2 규제(릿지) 추가
4. RFE (Recursive Feature Elimination)
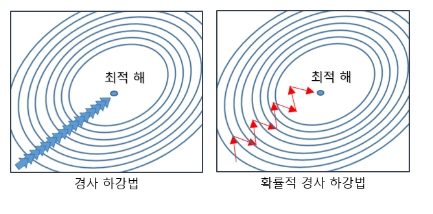
★ 다음은 확률적 경사 하강법 (SGD)에 대한 설명이다. ( ) 안에 들어갈 올바른 용어는?
| - 확률적 경사 하강법 (Stochastic Gradient Descent; SGD) 이란 손실 함수의 기울기를 구하여, 그 기울기를 따라 조금씩 아래로 내려가 최종적으로는 손실 함수가 가장 작은 지점에 도달하도록 하는 알고리즘이다 - 손실 함수 그래프에서 ( A ) 에 갇혀 ( B ) 을 찾지 못하는 경우가 많고, 손실 함수가 비등방성 함수일 때에서는 최적화에 있어 매우 비효율적이고 오래 걸리는 탐색 경로를 보여준다. |
1. A: 전역 극소점, B: 지역 최대점
2. A: 지역 최대점, B: 전역 극소점
3. A: 전역 극소점, B: 지역 극소점
4. A: 지역 극소점, B: 전역 극소점
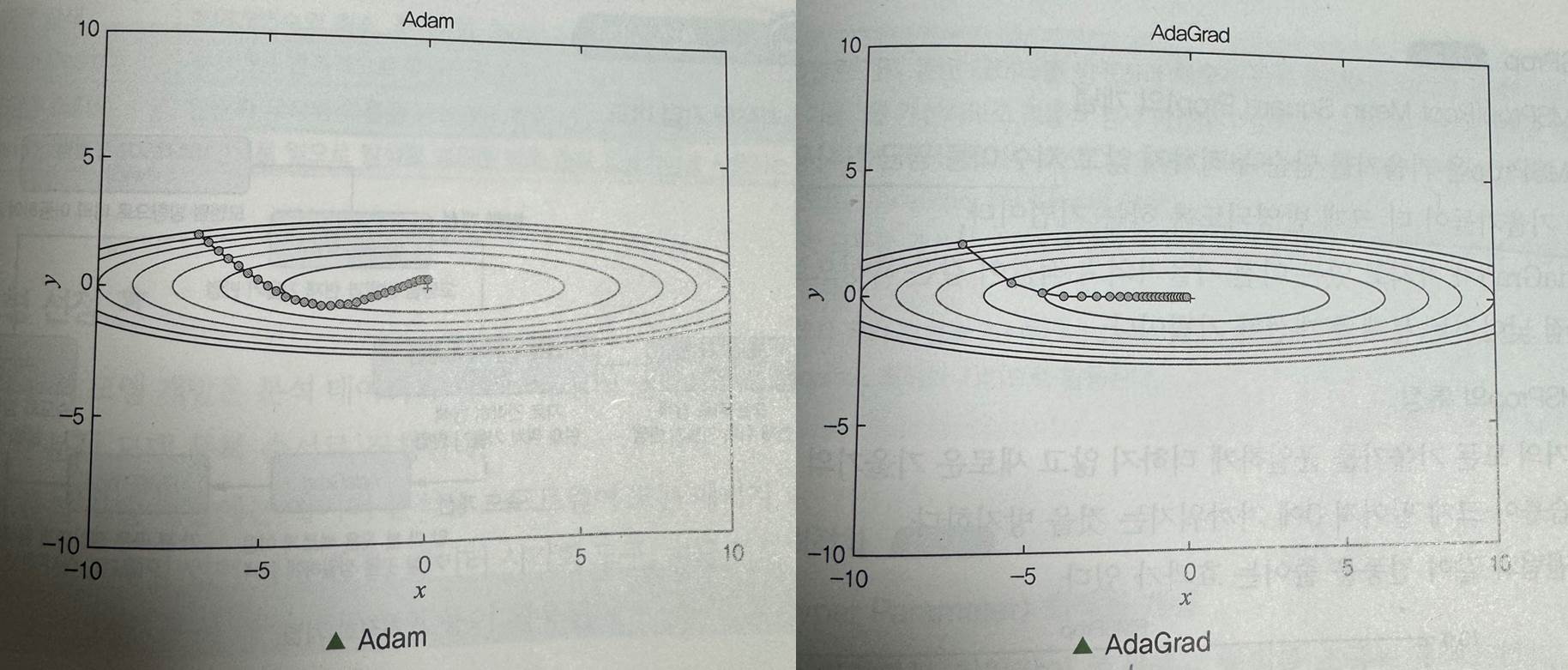
[매개 변수 최적화 기법]


★ 다음 중 인공신경망에서 Dropout과 같은 효과를 나타내는 것은?
1. 학습률 조정
2. 활성화 함수 변경
3. 은닉층 수 감소
4. 부스팅
▶ Dropout: 인공신경망에서 과대적합을 방지하기 위해 사용, (은닉층 수 감소 역시 과대적합 방지 위한 방법)
※ 과대적합: 제한된 훈련 데이터 세트가 지나치게 특화되어 새로운 데이터에 대한 오차가 매우 커지는 현상
(모델의 매개변수 수가 많거나 훈련 데이터 세트의 양이 부족한 경우에 발생)
- 방지 기법에는 데이터 증강, 모델의 복잡도 감소, 가중치 규제 적용 (릿지, 라쏘, 엘라스틱 넷) 등 있음.
★ 다음 중 인공신경망의 복잡도를 결정하는 것은?
1. 은닉층의 수
2. 비용 함수
3. 손실 함수
4. 노이즈
▶ 인공신경망의 복잡도는 은닉층의 수나 모델의 수용력 등으로 결정

★ 다음 중 비교 시각화의 유형으로, 설명 변수가 늘어날 때마다 축이 늘어나는 시각화 방법은?
1. 플로팅 바 차트
2. 막대 차트
3. 스타 차트
4. 히트맵
▶ 스타 차트: 각 변수를 표시 지점을 연결선을 통해 그려 별 모양의 도형으로 나타낸 차트
*설명 변수가 늘어날수록 축이 늘어남
★ 다음에서 설명하는 시각화 기법은?
| - 여러 축을 평행으로 배치하는 비교 시각화 기술 - 수직선엔 변수를 배치 - 측정 대상은 변수값에 따라 위아래로 이어지는 연결 선으로 표현 |
1. 산점도
2. 박스플룻
3. 스타 차트
4. 평행 좌표계
▶ 데이터 분석의 초기 단계에서 많은 변수 중 변수 간의 경향을 찾을 때 유용
★ 다음 중 히스토그램에 대한 설명으로 틀린 것은?
1. 질적, 양적 자료 표현에 사용
2. 종속변수를 확률 단위로도 표현 가능
3. 데이터 표현을 잘하려면 구간을 잘 정해야 함
4. 누적해서 표현하면 누적확률밀도함수를 항상 가짐
▶ 히스토그램은 양적 자료 표현에 사용
★ 다음 중 비교 시각화 유형에 대한 설명으로 가장 옳지 않은 것은?
1. 히트맵: 칸 별로 색상을 구분하여 데이터 값을 표현하는 시각화 그래프로 여러 가지 변수 비교 가능
2. 플로팅 바 차트: 막대가 가장 낮은 수치부터 가장 높은 수치까지 걸쳐있게 표현한 차트. 범주 내 값의 다양성, 중복 및 이상값 파악 가능
3. 체르포트 페이스; 데이터를 눈, 코, 귀, 입 등과 일대일 대응하여 얼굴 하나로 표현하는 시각화 방법
4. 스타 차트: 각 변수를 표시 지점을 연결선을 통해 그려 별 모양의 도형으로 나타낸 차트. 중심점은 축이 나타내는 값의 최대값, 가장 먼 끝점은 최소값 의미
▶ 스타 차타의 중심점 = 최소값, 가장 먼 끝점 = 최대값
| 시간 시각화 | - 시간에 따른 데이터의 변화 표현 - 시계열 데이터에서 주요 관심 요소는 경향성 - 개별적인 데이터보다는 전체적인 흐름 파악 필요 |
막대 그래프, 누적 막대 그래프, 선 그래프, 영역 차트, 계단식 그래프, 추세선 |
| 공간 시각화 | - 지도상에 해당하는 정보를 표현하는 시각화 방법 - 지도 위에 위치 표시를 위해 대부분 위도와 경도 이 |
등치지역도, 등치선도, 도트 플롯맵, 버블 플롯맵, 카토그램 등 |
| 분포 시각화 | - 데이터의 최대값, 최소값, 전체 분포 등을 나타냄 - 시계열 데이터와 비슷한, 구분 단위가 시간이 아니라 데이터가 차지하는 영역을 기준으로 한다는 점에서 차이 |
파이 차트, 도넛 차트, 트리맵, 누적 영역 차트 |
| 관계 시각화 | - 다변량 데이터 사이에 존재하는 변수 사이의 연관성, 분포와 패턴을 찾는 시각화 방법 - 상관관계: 변수 사이의 연관성 - 한 가지 요소의 변화가 다른 요소의 변화와 관련 있는지 표현하는 시각화 기법 |
산점도, 산점도 행렬, 버블 차트, 히스토그램, 네트워크 그래프 |
| 비교 시각화 | - 다변량 변수를 갖는 자료를 제한된 2차원에 효과적으로 표현하는 시각화 방법 | 플로팅 바 차트(간트 차트), 히트맵, 체르노프 페이스, 스타 차트, 평행 좌표 그래프 등 |
★ 다음 중 인포그래픽의 유형으로 가장 거리가 먼 것은?
1. 지도형 (연예인 선호도, 매장분포)
2. 도표형 (대부분의 수치 데이터)
3. 스토리텔링형 (유명인사, 기업정보 뉴스)
4. 문자형 (텍스트 중심의 정보)
[인포그래픽]

[4과목 정리]
[빅데이터 분석기사] 4과목 빅데이터 결과 해석(1)
[목차] [빅데이터 분석기사] 시험 과목 및 주요 내용 (필기) 빅데이터 분석기사 (필기) 시험 과목 및 주요 내용 출처: 데이터자격검정 (dataq.or.kr) 필기과목명 주요항목 세부항목 세세항목 빅데이터
puppy-foot-it.tistory.com
[빅데이터 분석기사] 4과목 빅데이터 결과 해석(2)
[목차] [빅데이터 분석기사] 시험 과목 및 주요 내용 (필기) 빅데이터 분석기사 (필기) 시험 과목 및 주요 내용 출처: 데이터자격검정 (dataq.or.kr) 필기과목명 주요항목 세부항목 세세항목 빅데이터
puppy-foot-it.tistory.com
'자격증 > 빅데이터분석기사' 카테고리의 다른 글
| [빅데이터 분석기사] 3과목 기출문제 오답노트 (1) | 2024.03.24 |
|---|---|
| [빅데이터 분석기사] 2과목 기출문제 오답노트 (1) | 2024.03.23 |
| [빅데이터 분석기사] 1과목 기출 문제 오답노트 (0) | 2024.03.16 |
| [빅데이터 분석기사] 4과목 빅데이터 결과 해석(2) (0) | 2024.03.16 |
| [빅데이터 분석기사] 4과목 빅데이터 결과 해석(1) (0) | 2024.03.15 |


