정수론
숫자를 특정 방식으로 설계한 이유와 숫자 자체에 대해 생각하는 수학의 영역
[숫자 체계]
1. 자연수
양수 - 예. 1, 2, 3, 4
2. 범자연수
자연수 + 0
9보다 큰 숫자에서 비어 있는 열의 자리를 표시하기 위해 개발
3. 정수
범자연수 + 음수의 자연수
음수(-, 마이너스) - 예. -1, -2, -3, -4
음수는 이익과 손실을 측정하는 재무 분야에서 유용
4. 유리수
분수로 표현할 수 있는 모든 숫자 + 유한소수 + 정수
유리수는 비율로 나타낼 수 있기 때문에 유비수 라고도 부름.
시간, 자원 등을 언제나 이산적인 단위로 측정할 수 없으므로 유리수가 필요
예 - 3/4, 6.5, 2/1=2
5. 무리수
분수로 표현할 수 없으며, 소수점 자릿수가 무한대로 늘어날 수 있다.
대표적인 무리수 - π(파이), √ (루트, 제곱근), e(오일러의 수, 자연상수)
★ 오일러의 수: 자연로그의 밑이 되는 자연상수 e를 오일러의 수라 하며 e=2.71828···의 값을 가지는 무리수이다.
6. 실수
유리수 + 무리수
7. 복소수와 허수
1) 허수: - 음수의 제곱근
2) 복소수: -1 미만의 모든 마이너스 수에 대한 수학적 공리의 문제를 피하기 위해, 허수를 가지고 만든 식으로, 이 식을 하나의 숫자로 취급.
대부분의 데이터 과학 작업에서는
범자연수, 자연수, 정수와 실수를 사용한다.
연산 순서
수식의 연산순서는
괄호 → 지수 → 곱셈 → 나눗셈 → 덧셈 → 뺄셈 순으로, 왼쪽에서 오른쪽으로 계산한다.
해당 단어들의 앞글자를 따면
PEMDAS
P - Parentheses, 괄호
E - Exponent, 지수
M - Multiply, 곱셈
D - Divide, 나눗셈
A - Add, 덧셈
S - Subtract, 뺄셈
PEMDAS 로 연산의 순서를 기억
예를 들어, 아래와 같은 식을 계산한다고 한다면
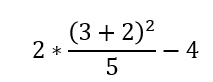
1) 괄호 계산: 3+2=5
2) 5를 제곱해 지수 계산: 5*5 = 25
3) 곱셈 계산: 2*25/5 = 50/5
4) 나눗셈 계산: 50/5 = 10
5) 덧셈(또는 뺄셈) 계산: 10-4 = 6
이를 파이썬으로 계산할 때에는 아래와 같이 입력하면 된다.
my_value = 2 * (3+2)**2 / 5 -4
print(my_value)
정답은 6.0
★ 보다 복잡한 표현식에서는 괄호를 사용해 연산 순서를 제어하는 것이 좋다.
따라서, 아래와 같이 괄호를 통해 연산 순서를 명확히 해주는게 좋다.
# 보다 정확하게
my_value = 2 * ((3+2)**2 / 5) -4
print(my_value)변수
수학에서 변수란,
지정되지 않았거나 알 수 없는 숫자를 나타내는 이름있는 플레이스홀더(Named Placeholder) 라고 정의한다.
어떤 실수를 나타내는 변수 x가 있을 때 그 변수가 무엇인지 지정하지 않고도 곱할 수 있다.
# 변수
x = int(input("숫자를 입력하시오"))
number = 3 * x
print(number)
[특정 변수 유형을 위한 표준적인 변수 이름]
θ (세타): 각도를 나타냄. > 파이썬에서는 theta 로 지정하여 사용
β (베타): 선형 회귀의 매개변수 > 파이썬에서는 beta 로 지정하여 사용
[변수 이름에 첨자 붙이기]
변수 이름에 첨자를 붙여 하나의 변수 이름에 대한 여러 인스턴스를 나타낼 수 있다.
ex) x1, x2, x3, ... x_1, x_2, x_3, ...
함수(function)
함수는 두 개 이상의 변수 간의 관계를 정의한다.
구체적으로, 함수는 입력 변수를 받아 표현식에 연결한 다음, 출력 변수를 생성한다.
입력 변수(input variable)는 도메인 변수(domain variable) 또는 독립 변수(independent variable),
출력 변수(output variable)는 종속 변수(dependent variable)이라고 부르기도 한다.
함수는 변수 간의 예측 가능한 관계를 모델링하기 때문에 유용하다.
y = 2x + 1 이라는 간단한 선형 함수를 예로 들면,
x 값이 주어지면 x를 이용해 y 값을 구한다. (x는 독립 변수, y는 종속 변수)
종속 변수 y에 대한 또 다른 관례는 f(x)와 같이 명시적으로 x의 함수라고 쓰며,
f(x) = 2x + 1 이라고도 표현한다.
# 파이썬에서 선형 함수 선언하기
def f(x):
return 2 * x + 1
x_values = [0, 1, 2, 3]
for x in x_values:
y = f(x)
print(y)
합계 (시그마)
∑ (시그마): 원소들의 합
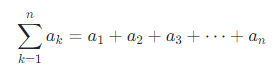
예제1)
예를 들어, 숫자 1부터 5까지의 각 숫자에 2를 곱한 다음 이를 모두 더하는 경우, 시그마를 사용하면 아래와 같이 표현할 수 있다.
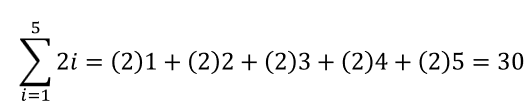
이를 파이썬으로 실행하면
# 시그마(원소들의 합)
summation = sum(2*i for i in range(1, 6))
# range 함수는 마지막 값 포함하지 않음. 1,6 = 1부터 5까지
print(summation)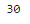
▶ i는 루프를 반복할 때 연속적인 인덱스 값을 나타내는 플레이스홀더 변수
예제2)
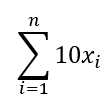
크기가 n인 숫자 배열을 반복하면서 각 숫자에 10을 곱한 다음 모두 더하시오.
이 경우, 파이썬을 사용해 네 개의 숫 자 배열에 이 표현식을 실행한다.
x = [1, 4, 6, 2]
n = len(x)
summation = sum(10*x[i] for i in range(0, n))
# 프로그래밍언어에서는 인덱스 0부터 시작
print(summation)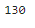
★ 합계 기호 ∑ 는 '여러 개를 더한다'는 의미이며, 인덱스 i와 최댓값 n을 사용해 합계에 들어가는 반복을 표현한다.
거듭제곱
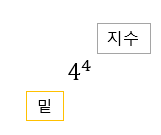
거듭제곱(exponentiation)은 지정된 횟수만큼 숫자를 곱하는 것이다.
예를 들어, 4의 4제곱은 4를 4번 곱하라는 뜻이다.
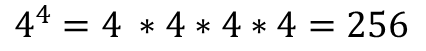
밑(base)은 거듭제곱하려는 변수 또는 값이며, 지수(exponent)는 밑을 곱하는 횟수이다.
지수를 단순한 곱셈으로 확장해서 하나의 지수로 통합하면 다음과 같다.
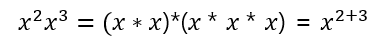
위처럼, 밑이 같은 거듭제곱을 곱할 때에는 단순히 지수를 더하면 되는데, 이를 지수 법칙이라고 한다.
◆ 거듭제곱의 나눗셈
x^2를 x^5 로 나누는 경우엔
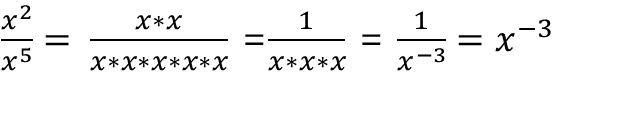
이 되는데, 분자와 분모 모두에 동일한 거듭제곱이 있으면 이를 상쇄할 수 있다.
또한, 지수가 음수일 때에도 지수 법칙을 적용할 수 있다.
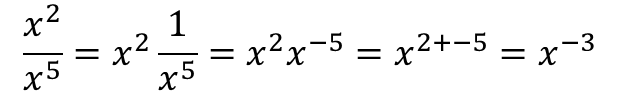
또한, 밑이 어떤 수든 지수가 0이면 결과값은 1이 된다. (a=b, b=c 이면 a=c 라는 등식의 성질에 따라)
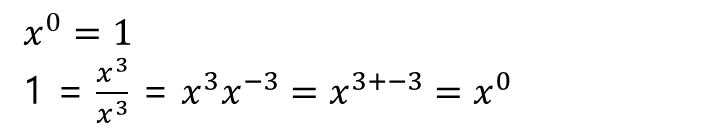
◆ 분수 지수
분수 지수는 제곱근과 같은 근을 표현하는 다른 방법이다.
예를 들어, √4 는 '어떤 숫자를 거듭 제곱하면 4가 되는가?' 라고 묻는 것이고, 답은 2이다.
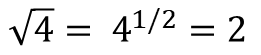
세제곱근은
제곱근과 비슷하지만 스스로를 세 번 곱해 결괏값이 되는 숫자를 구한다.
8의 세제곱근은 '스스로를 세 번 곱하면 8이 되는 숫자는 무엇인가?' 라고 묻는 것이다.

8의 세제곱근을 세 법 곱하면? 세제곱근은 사라지고 결괏값은 8이 된다.
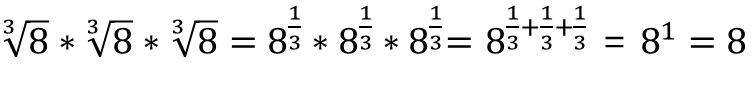
★ 거듭제곱의 거듭제곱
거듭제곱의 거듭제곱은 지수의 곱셈에 해당한다.
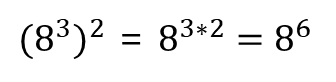
이를 좀 더 길게 풀어보면
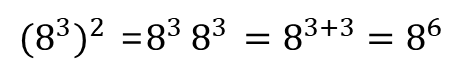
★ 분자가 1이 아닌 분수 지수
분자가 1이 아닌 분수 지수는 8의 세제곱근을 구한 다음 이를 제곱하는 것과 같다.
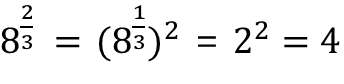
π 같은 무리수의 지수의 경우, 유리수로 근사해 게산한다.
즉, 소수점 이하 일정 자리까지만 계산한다.
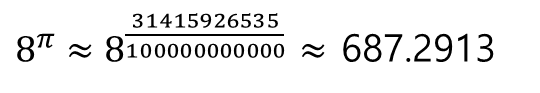
[출처]
네이버 지식백과
개발자를 위한 필수 수학
위키백과
나무위키
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [통계학] 자료 정리 - 2 (1) | 2024.10.03 |
|---|---|
| [통계학] 자료 정리 - 1 (4) | 2024.10.02 |
| [개발자를 위한 수학] 미분, 적분 (+파이썬) (5) | 2024.10.02 |
| [개발자를 위한 수학] 로그, 자연로그, 오일러 수 (+파이썬) (6) | 2024.10.02 |
| [통계학] 통계학의 기초개념 (0) | 2024.05.02 |


