미분
미분(derivative)은 함수의 기울기를 나타내며 함수의 어느 지점에서의 변화율을 측정하는 데 유용하다.
또한 미분은 머신러닝과 수학 알고리즘, 특히 경사 하강법에 사용된다.
경사 하강법을 간단히 말하자면, 기울기가 0이면 출력 변수의 최솟값 또는 최댓값에 도달했음을 의미한다.
[파이썬 머신러닝] 경사 하강법(GD, gradient descent)
경사하강법 경사하강법(GD, gradient descent)은 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘이다. 경사 하강법의 기본 아이디어는 비용 함수를 최소화하기 위해 반
puppy-foot-it.tistory.com
이 개념은 선형 회귀, 로지스틱 회귀, 신경망 등을 배울 때 매우 유용하다.
f(x) = x^2 함수의 그래프를 그려본다.
# 미분 그래프 그리기
from sympy import *
# x를 기호 변수로 정의
x = symbols('x')
f = x**2
# 그래프 그리기
plot(f, (x, -10, 10), title='f(x)=x**2 Graph', xlabel='x', ylabel='f(x)')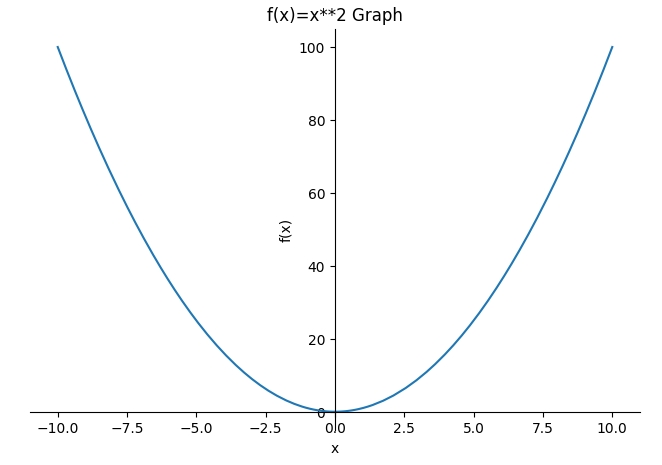
x=2 에서 곡선이 얼마나 '가파른'지 정도를 측정해 접선으로 시각화해 본다.
★ 접선(tangent line): 주어진 지점에서 커브에 살짝 닿는 직선. 접선을 통해 주어진 지점에서의 기울기도 계산 가능하며, 함수에서 x 값과 이 값에 매우 가까운 점을 지나는 직선을 그어 주어진 x값의 접선을 추정할 수 있다.
# f(x) = x**2 함수
from sympy import *
# x를 기호 변수로 정의
x = symbols('x')
f = x**2
# 함수 그래프 그리기
p1 = plot(f, (x, -10, 10), show=False, title='Graph of f(x) = x^2 with Tangent at x=2', xlabel='x', ylabel='f(x)')
# f(x)의 도함수(기울기) 찾기
f_prime = diff(f, x)
# x=2에서 기울기 계산
slope_at_2 = f_prime.subs(x, 2)
print(f"Slope at x=2: {slope_at_2}")
# x=2에서 접선 방정식을 정의
tangent_line = slope_at_2 * (x - 2) + f.subs(x, 2)
# 접선 그리기
p2 = plot(tangent_line, (x, -10, 10), line_color='red', show=False)
# 그래프 결합하기
p1.extend(p2)
p1.show()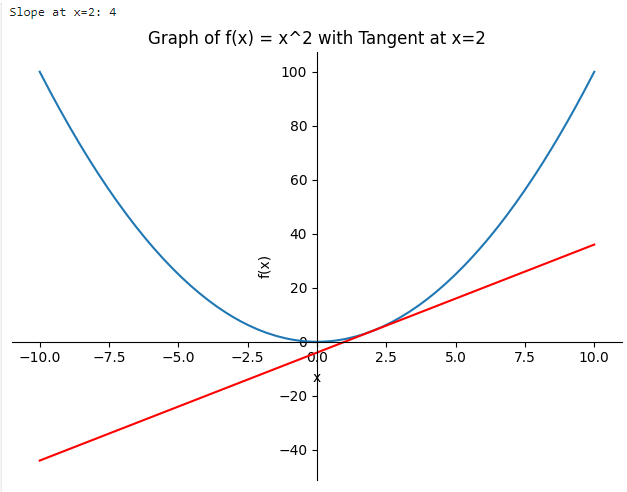
x = 2와 이에 가까운 값인 x = 2.1을 함수 f(x) = x^2 에 전달하면 f(2) =와 f(2.1)=4.41 을 얻는다. 또한, 이 두 점을 통과하는 직선의 기울기는 4.1이다.
간단한 기울기 공식을 사용하면 두 지점 사이의 기울기 m을 계산할 수 있다.
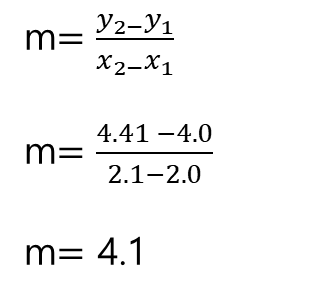
두 점 사이의 x 간격을 x = 2와 x=2.00001 처럼 더 작게 만들면 f(2) = 4와 f(2.00001) = 4.00004가 되므로 실제 기울기인 4에 매우 가까워 진다. 따라서 인접한 값과의 간격이 작을수록 주어진 지점에서 곡선의 기울기에 더 가까워진다.
[파이썬으로 미분 계산하는 코드]
# 파이썬으로 미분 계산하기
def derivative_x(f, x, step_size):
m = (f(x + step_size) - f(x)) / ((x + step_size) - x)
return m
def my_function(x):
return x**2
slope_at_2 = derivative_x(my_function, 2, 0.00001)
print(slope_at_2)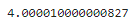
◆ 기울기를 계산하는 더 좋은 방법
함수 f(x) = x^2 의 도함수(derivative function)을 만들려면 지수를 곱셈 계수로 내리고 원래 지수는 1 감소시킨다.

따라서 x = 2 에서 기울기를 구하고 싶고 도함수가 있다면 해당 x 값을 도함수에 입력해 기울기를 구한다.
★ 도함수: 어떤 입력에 대한 함수의 순간 변화율 또는 그 지점에서 접선의 기울기를 나타내는 함수.
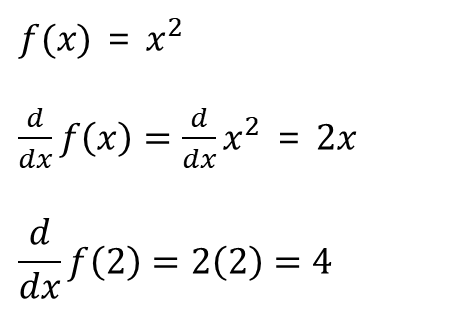
심파이는 기호 계산을 사용해 도함수를 구하는 좋은 도구이며, 무료 오픈 소스이다.
[심파이에서 도함수 계산하기]
# 심파이에서 도함수 계산하기
from sympy import *
# 'x' 선언
x = symbols('x')
# 파이썬 표현식을 사용해 함수 정의
f = x**2
# 이 함수의 도함수 계산
dx_f = diff(f)
print(dx_f)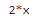
심파이에서 symbols() 함수로 변수를 선언하면 일반 파이썬 구문을 사용해 함수를 정의할 수 있다.
그런 다음 diff() 를 사용해 도함수를 계산한다.
심파이를 계속 사용하고 싶다면 subs() 함수를 호출해 x 변수를 다른 값으로 바꿀 수 있다.
# 파이썬으로 미분 계산하기_2
def f(x):
return x**2
def d_f(x):
return 2*x
slope_at_2 = d_f(2.0)
print(slope_at_2)
[심파이의 치환 기능 사용하기]
# x = 2에서 기울기 계산하기
print(dx_f.subs(x, 2))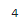
편도함수
편도함수(partial derivative): 여러 입력 변수가 있는 함수의 도함수.
예를 들어 1차원 함수의 기울기가 아니라 여러 변수에 대해 여러 방향의 기울기가 있다. 주어진 변수의 도함수에서 다른 변수는 일정하게 유지된다고 가정한다.
f(x,y) = 2x^3 + 3y^3 함수에서 x와 y 변수는 각각 고유한 도함수를 갖고, 이는 다차원 곡면에서 각 변수에 대한 기울기를 나타낸다. 다차원을 다룰 때는 기술적으로는 이 기울기를 그래디언트(gradient)라고 부른다.
[x와 y에 대한 도함수]
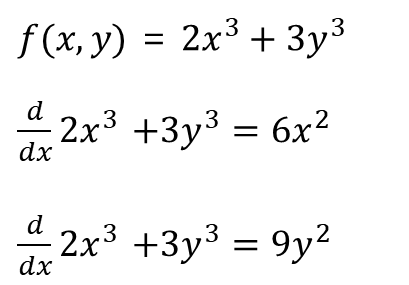
다음은 심파이를 이용해 각각 x와 y에 대한 편도함수를 계산하는 방법이다.
# 심파이로 편도함수 계산하기
from sympy import *
from sympy.plotting import plot3d
# x와 y를 심파이에 선언
x,y = symbols('x y')
# 파이썬 표현식을 사용헤 함수 정의
f = 2*x**3 + 3*y**3
# x와 y에 대한 편도함수 계산
dx_f = diff(f, x)
dy_f = diff(f, y)
print(dx_f)
print(dy_f)
# 함수 그래프 그리기
plot3d(f)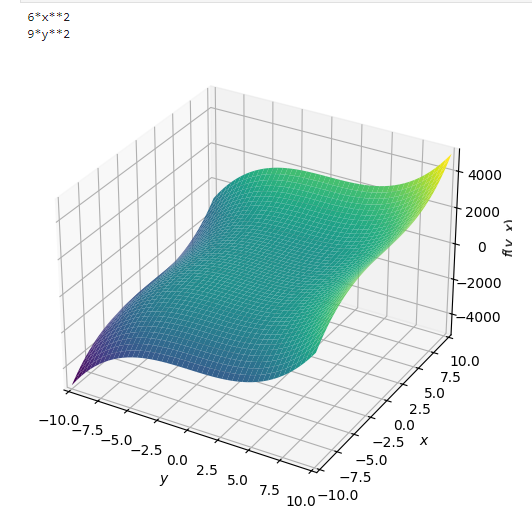
따라서 x, y이 값이 1,2 인 경우 x 에 대한 기울기는 6(1)^2 = 6,
y에 대한 기울기는 9(2)^2 = 36이다.
연쇄 법칙
신경망을 만들 때 연쇄 법칙(chain rule) 이라는 특별한 수학 기법이 필요하다. 신경망 층을 훈련할 때 각 층의 도함수를 풀어 연결해야 한다. 연쇄 법칙은 신경망을 훈련할 대 적절한 가중치와 편향을 갖도록 하는 데 핵심이 되는 부분이다. 양파처럼 겹겹이 쌓인 노드의 도함수를 구하는 대신, 각 노드의 도함수를 곱해서 계산하면 훨씬 쉽게 계산할 수 있다.
◆ 간단한 대수학 예제를 통한 연쇄 법칙 학습
다음 함수 두 개가 주어졌다고 가정해본다.
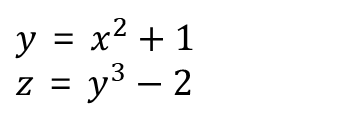
첫 번째 함수에서 y는 출력 변수이나, 두 번째 함수에서는 입력 변수이기 때문에 이 두 함수는 연결되어 있다.
즉, 첫 번째 함수 y를 두 번째 함수 z에 다음과 같이 대입할 수 있다.
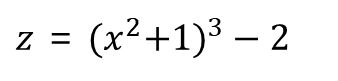
x에 대한 z의 도함수는 아래와 같이 구할 수 있다.
# x에 대한 z의 도함수
from sympy import *
x = symbols('x')
z = (x**2 + 1)**3 - 2
dz_dx = diff(z, x)
print(dz_dx)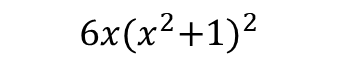
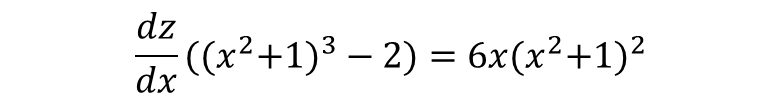
◆ 연쇄 법칙을 활용한 방식
y와 z 함수의 도함수를 따로따로 구한 다음, 이를 곱하면 x에 대한 z의 도함수를 구할 수 있다.
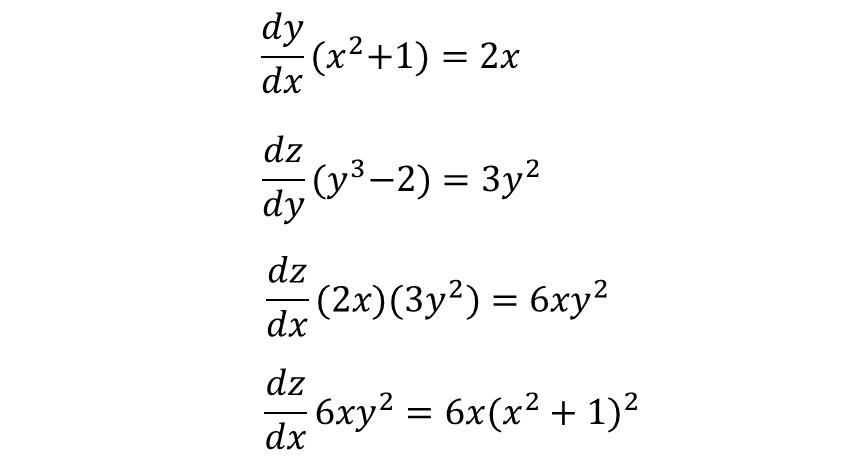
▶ (x가 입력 변수인) 함수 y가 (y가 입력 변수인) 다른 함수 z를 구성한다면 두 개의 개별 도함수를 곱해서 x에 대한 z의 도함수를 구할 수 있다.
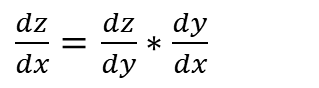
연쇄 법칙을 사용한 도함수는 변수를 대체한 함수의 도함수와 같다.
[연쇄 법칙 증명을 위한 심파이 코드]
# 연쇄 법칙 증명을 위한 심파이 코드
from sympy import *
x, y = symbols('x y')
# 첫 번째 함수 도함수 (충돌을 피하기 위해 _y로 기업)
_y = x**2 + 1
dy_dx = diff(_y)
# 두 번째 도함수
z = y**3 -2
dz_dy = diff(z)
# 연쇄법칙을 사용한 경우와 대체 방식을 사용한 경우 도함수 계산
dz_dx_chain = (dy_dx * dz_dy).subs(y, _y)
dz_dx_no_chain = diff(z.subs(y, _y))
# 두 값이 같은 경우 연쇄 법칙 증명됨
print('연쇄 법칙:', dz_dx_chain)
print('대체 법칙:', dz_dx_no_chain)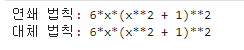
적분
적분(integral): 미분의 반대, 주어진 범위에서 곡선 아래의 면적을 구한다.
보통 데이터 과학이나 머신러닝에서는 (예. 확률 분포의 아래쪽 면적 구하기) 적분을 직접 사용하지 않고 이미 적분으로 계산된 누적 분포 함수(cumulative distribution function, CDF)를 사용한다.
예를 들어 f(x) = 2x 함수의 0과 1 사이의 선 아래 면적을 구한다고 할 경우,
0.0과 1.0 범위에서 직선과 x축 사이의 면적을 계산하려고 한다. 이 경우 삼각형 면적 A를 구하는 공식은 아래와 같다.
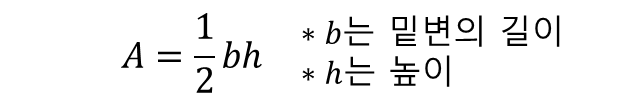
예를 들어, 높이가 2, 면적이 1인 삼각형 면적의 경우에는 매우 간단하게 계산이 된다.
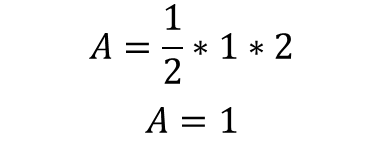
그러나, 비선형 함수 아래의 면적 계산은 매우 어렵다.
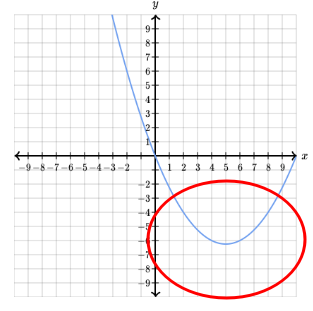
이러한 경우 곡선 때문에 면적을 구할 수 있는 깔끔한 해결책은 없다.
그러나 곡선 아래에 직사각형을 배치하고 각 직사각형의 가운데가 곡선에 땋을 때까지 길이를 늘리는 방식으로 곡선 아래 면적의 근사치를 구할 수 있다.
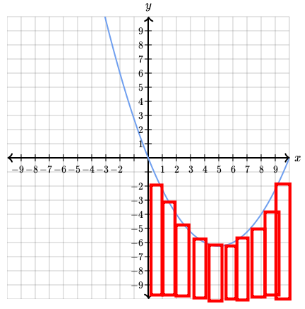
직사각형의 면적은 A = 길이 * 너비 이므로 각 직사각형의 넓이를 쉽게 합산할 수 있다.
이렇게 직사각형의 너비를 줄여 직사각형의 수를 100개, 1000개, 100000개 까지 늘리면 곡선 아래 영역에 더 가까워지는데,
이러한 방식으로 실젯값에 접근하기 위해 무언가를 무한하게 증가시키거나 감소시키는 방법을 사용할 수 있다.
[파이썬으로 적분 근사하기]
1) 직사각형 5개
# 파이썬으로 적분 근사하기
def approximate_integral(a, b, n, f):
delta_x = (b - a) / n
total_sum = 0
for i in range(1, n + 1):
midpoint = 0.5 * (2 * a + delta_x * (2 * i - 1))
total_sum += f(midpoint)
return total_sum * delta_x
def my_function(x):
return x**2 + 1
# 직사각형 5개로 계산하기
area = approximate_integral(a=0, b=1, n=5, f=my_function)
print(area)
2) 직사각형 1,000개
# 직사각형 1000개로 계산하기
area = approximate_integral(a=0, b=1, n=1000, f=my_function)
print(area)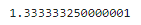
▶ 정밀도가 조금 더 높아지고 소수점 이하 자릿수가 늘어났다.
3) 직사각형 1,000,000개
# 직사각형 1,000,000개로 계산하기
area = approximate_integral(a=0, b=1, n=1000000, f=my_function)
print(area)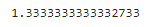
▶ 증가폭이 줄어들고 '.333'이 계속 반복되는 값에 수렴한다.
직사각형 개수가 늘어남에 따라 점점 더 작은 소수점 위치에서 극한에 다다른다.
[심파이를 사용해 적분 수행하기]
유리수를 지원하는 심파이를 사용해 더 정확한 접근 방식을 시도해본다.
# 심파이를 사용해 적분 수행하기
from sympy import *
# 심파이에 'x' 선언
x = symbols('x')
# 파이썬 표현식을 사용해 함수 정의
f = x**2 + 1
# x=0과 1 사이의 면적을 구하기 위해 x에 대해서 함수의 적분 계산
area = integrate(f, (x, 0, 1))
print(area)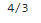
실제 면적은 4/3= 1.3333..... 이다.
[출처]
개발자를 위한 필수 수학
네이버 지식백과
나무위키
위키백과
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [통계학] 자료 정리 - 2 (1) | 2024.10.03 |
|---|---|
| [통계학] 자료 정리 - 1 (4) | 2024.10.02 |
| [개발자를 위한 수학] 로그, 자연로그, 오일러 수 (+파이썬) (6) | 2024.10.02 |
| [개발자를 위한 수학] 기초수학 (+파이썬) (0) | 2024.10.02 |
| [통계학] 통계학의 기초개념 (0) | 2024.05.02 |



