경사하강법
경사하강법(GD, gradient descent)은 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘이다. 경사 하강법의 기본 아이디어는 비용 함수를 최소화하기 위해 반복해서 파라미터를 조정해 가는 것이다.
파라미터 벡터에 대해 비용 함수의 현재 그레이디언트를 계산하고 그 그레이디언트가 감소하는 방향으로 진행한다. 이 그레이디언트가 0이 되면 최소값에 도달한 것이다.
머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 비용 함수가 반환하는 오류 값을 지속해서 감소시키고 최종적으로는 더 이상 감소하지 않는 최소의 오류 값을 구하는 것인데, 어떻게 비용 함수가 최소가 되는 W 파라미터를 구할 수 있을까?
★ W 파라미터 (Weight) : 가중치
W 파라미터의 개수가 적다면 고차원 방정식으로 비용 함수가 되는 W 변숫값을 도출할 수 있겠지만, W 파라미터가 많으면 고차원 방정식을 동원하더라도 해결하기가 어렵다. 경사 하강법은 이러한 고차원 방정식에 대한 문제를 해결해 주면서 비용 함수 RSS를 최소화하는 방법을 직관적으로 제공하는 뛰어난 방식이다.
경사 하강법은 '점진적으로' 반복적인 계산을 통해 W 파라미터 값을 업데이트하면서 오류 값이 최소가 되는 W 파라미터를 구하는 방식이다. 이 방법은 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 W 파라미터를 지속해서 보정해 나간다. 그리고 오류 값이 더 이상 작아지지 않으면 그 오류 값을 최소 비용으로 판단하고 그때의 W 값을 최적 파라미터로 반환한다.
경사하강법과 학습률
경사 하강법에서 중요한 파라미터는 스텝의 크기로, 학습률 하이퍼파라미터로 결정된다. 학습률이 너무 작으면 알고리즘이 수렴하기 위해 반복을 많이 진행해야 하므로 시간이 오래 걸린다.
한편 학습률이 너무 크면 골짜기를 가로질러 반대편으로 건너뛰게 되어 이전보다 더 높은 곳으로 올라가게 될지도 모른다. 이는 알고리즘을 더 큰 값으로 발산하게 만들어 적절한 해법을 찾지 못하게 된다.

모든 비용 함수가 위의 이미지처럼 매끈한 그릇 같지는 않다.
패인 곳, 평지 등 특이한 지형이 있으면 최솟값으로 수렴하기가 매우 어렵다.

위의 이미지는 경사 하강법의 두 가지 문제점을 보여준다.
1) 랜덤 초기화 때문에 알고리즘이 왼쪽에서 시작하면 전역 최솟값 보다 덜 좋은 지역 최솟값에 수렴한다.
2) 알고리즘이 오른쪽에서 시작하면 평탄한 지역을 지나기 위해 시간이 오래 걸리고 일찍 멈추게 되어 전역 최솟값에 도달하지 못한다.
- 전역 최솟값(global minimum): 전체 구간에서의 최솟값
- 지역 최솟값(local minimum): 함수의 일부 구간에서의 최솟값
다행히 선형 회귀를 위한 MSE 비용 함수는 곡선에서 어떤 두 점을 선택해 선을 그어도 곡선을 가로지르지 않는 블록 함수이다. 이는 지역 최솟값이 없고 하나의 전역 최솟값만 있다는 뜻이며, 연속된 함수이고 기울기가 갑자기 변하지 않는다.
경사하강법 코드 구현
간단한 회귀식인 y = 4X + 6을 근사하기 위한 100개의 데이터 세트를 만들고, 여기에 경사 하강법을 이용해 회귀 계수를 도출한다. (주피터 노트북, 파이썬 코드)
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
# y=4x+6 을 근사(w1=4, w0=6). 임의의 값은 노이즈를 위해 만듦.
X = 2 * np.random.rand(100,1)
y = 6 +4 * X+np.random.randn(100,1)
# X, y 데이터 세트 산점도로 시각화
plt.scatter(X, y)
데이터는 y = 4X + 6을 중심으로 무작위로 퍼져 있다.
◆ 비용 함수 정의
비용 함수 get_cost()는 실제 y 값과 예측된 y 값을 인자로 받아서 (실제값i - 예측값i)^2(제곱) 을 계산해 반환한다.
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
◆ 경사 하강법 구현
경사 하강법을 gradient_descent()라는 함수를 생성해 구현.
gradient_descent()는 위에서 무작위로 생성한 X와 y를 입력받는데, X와 y 모두 넘파이 ndarray 이다.
#w1과 w0를 업데이트할 w1_update, w0_update를 반환
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N=len(y)
#먼저 w1_update, w0_update를 각각 w1, w0의 shape와 동일한 크기를 가진 0 값으로 초기화
w1_update = np.zeros_like(w1)
w2_update = np.zeros_like(w0)
#예측 배열 계산하고 예측과 실제 값의 차이 계산
y_pred = np.dot(X, w1.T) + w0
diff = y-y_pred
#w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진 행렬 생성
w0_factors = np.ones((N, 1))
#w1과 w0을 업데이트할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1_update, w0_update
◆ gradient_descent_steps() 함수 생성
get_weight_updates() 을 경사 하강 방식으로 반복적으로 수행하여 w1과 w0을 업데이트하는 함수
#입력 인자 iters로 주어진 횟수만큼 반복적으로 w1과 w0를 업데이트 적용
def gradient_descent_steps(X, y, iters=10000):
#w0와 w1을 모두 0으로 초기화
w0 = np.zeros((1, 1))
w1 = np.zeros((1, 1))
#인자로 주어진 iters 만큼 반복적으로 get_weight_updates() 호출해 w1, w0 업데이트 수행.
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
◆ gradient_descent_steps() 함수 호출하여 w1, w0 산출 및 예측 오류 계산
w1, w0 산출 후 예측값과 실제값의 RSS 차이를 계산하는 get_cost() 함수를 생성하고 이를 이용해 경사 하강법의 예측 오류 계산
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
w1, w0 = gradient_descent_steps(X, y, iters=1000)
print("w1:{0:3f} w0:{1:3f}".format(w1[0, 0], w0[0, 0]))
y_pred = w1[0, 0] * X + w0
print('Gradient Descent Total Cost:{0:4f}'.format(get_cost(y, y_pred)))
실제 선형식인 y = 4X+6 과 유사하게 w1은 4.022, w0는 6.162가 도출되었고, 예측 오류 비용은 약 0.9935이다.
◆ 회귀선 그리기
앞서 구한 y_pred를 기반으로 회귀선을 그려본다.
plt.scatter(X, y)
plt.plot(X, y_pred)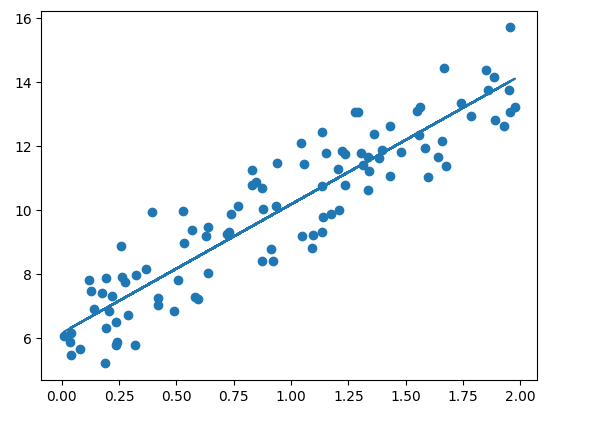
배치 경사 하강법
경사 하강법을 구현하려면 각 모델 파라미터에 대해 비용 함수의 그레이디언트를 계산해야 한다. 다시 말해 파라미터가 조금 변경될 때 비용 함수가 얼마나 바뀌는지를 계산해야 하고, 이를 편도함수 (partial derivative)라고 한다.
이는 '동쪽을 바라봤을 때 발밑에 느껴지는 산의 기울기는 얼마인가?'와 같은 질문이며, 같은 질문을 북쪽에 대해서도 한다. 만약 3차원 이상의 세상이라 가정하면 다른 모든 차원에 대해 반복한다.
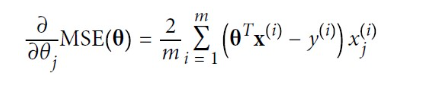
편도함수를 각각 계산하는 대신 아래의 식을 사용하여 한꺼번에 계산할 수 있다. 그레이언트 벡터는 비용 함수의 모델 파라미터마다 한 개씩인 편도함수를 모두 담고 있다.
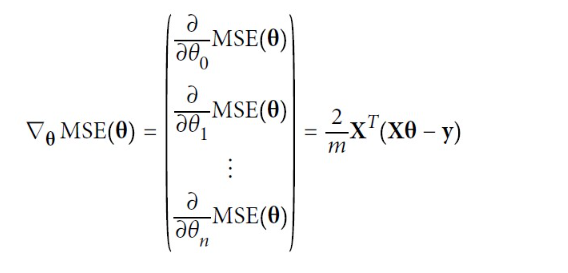
▶ 이 공식은 매 경사 하강법 스텝에서 전체 훈련 세트X에 대해 계산하기 때문에 이 알고리즘을 배치 경사 하강법(batch gradient descent)이라고 한다. 즉, 매 스텝에서 훈련 데이터 전체를 사용하여 이런 이유로 매우 큰 훈련 세트에서는 아주 느리다.
확률적 경사 하강법
일반적으로 경사 하강법은 모든 학습 데이터에 대해 반복적으로 비용함수 최소화를 위한 값을 업데이트하기 때문에 훈련 세트가 커지면 수행 시간이 매우 오래 걸린다는 단점이 있다. 그 때문에 실전에서는 대부분 확률적 경사 하강법(Stochastic Gradient Descent)을 이용한다.
확률적 경사 하강법은 전체 입력 데이터로 w가 업데이트되는 값을 계산하는 것이 아니라 일부 데이터만 이용해 w가 업데이트되는 값을 계산하므로 경사 하강법에 비해서 빠른 속도를 보장한다. 확률적 경사 하강법은 매 스텝에서 한 개의 샘플을 랜덤으로 선택하고 그 하나의 샘플에 대한 그레이디언트를 계산한다. 한 번에 하나의 샘플을 처리하면 매 반복에서 다뤄야 할 데이터가 매우 적기 때문에 알고리즘이 확실히 빠르고, 매 반복에서 하나의 샘플만 메모리에 있으면 되므로 매우 큰 훈련 세트도 훈련시킬 수 있다. 따라서 대용량의 데이터의 경우 대부분 확률적 경사 하강법이나 미니 배치 확률적 경사 하강법을 이용해 최적 비용함수를 도출한다.
반면 확률적(랜덤)이므로 이 알고리즘은 배치 경사 하강법보다 훨씬 불안정하다. 비용 함수가 최솟값에 다다를 때까지 부드럽게 감소하지 않고 위아래로 요동치며 평균적으로 감소한다. 시간이 지나면 최솟값에 매우 근접하겠지만 계속 요동쳐 최솟값에 안착하지 못한다. 알고리즘이 멈추면 좋은 파라미터가 구해지겠지만 최적치는 아닌 셈이다.
무작위성은 지역 최솟값에서 탈출시켜줘서 좋지만 알고리즘을 전역 최솟값에 다다르지 못하게 한다는 점에서는 좋지 않다. 이 딜레마를 해결하는 한 가지 방법은 학습률을 점진적으로 감소시키는 것이다. 시작할 때는 학습률을 크게 하고, 점차 작게 줄여서 알고리즘이 전역 최솟값에 도달하게 한다. 매 반복에서 학습률을 결정하는 함수를 학습 스케줄(learning schedule) 이라고 한다.
학습률이 너무 빨리 줄어들면 지역 최솟값에 갇히거나 최솟값까지 가는 중간에 멈춰 버릴 수도 있다.
학습률이 너무 천천히 줄어들면 오랫동안 최솟값 주변을 맴돌거나 훈련을 너무 일찍 중지해서 지역 최솟값에 머무를 수 있다.
(미니 배치) 확률적 경사 하강법의 구현
◆ stochastic_gradient_descent_steps() 함수로 구현
이 함수는 앞서 생성한 gradient_descent_steps() 함수와 크게 다르지 않으나, 전체 X, y 데이터에서 랜덤하게 batch_size(배치사이즈) 만큼 데이터를 추출해 이를 기반으로 w1_update, w0_update를 계산하는 부분만 차이가 있다.
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1, 1))
w1 = np.zeros((1, 1))
for ind in range(iters):
np.random.seed(ind)
#전체 X, y 데이터에서 랜덤하게 batch_size 만큼 데이터를 추출해 sample_X, sample_y로 저장
stochastic_random_index = np.random.permutation(X.shape[0])
sample_X = X[stochastic_random_index[0:batch_size]]
sample_y = y[stochastic_random_index[0:batch_size]]
#랜덤하게 batch_size만큼 추출된 데이터 기반으로 w1_update, w0_update 계산 후 업데이트
w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
◆ 함수로 w1, w0 및 예측 오류 비용 계산
w1, w0 = stochastic_gradient_descent_steps(X, y, iters=1000)
print("w1:", round(w1[0, 0], 3), "w0:", round(w0[0, 0], 3))
y_pred = w1[0, 0] * X + w0
print('Stochastic Gradient Descent Total Cost: {0:4f}'.format(get_cost(y, y_pred)))
▶ (미니 배치) 확률적 경사 하강법으로 구한 w0, w1 결과는 경사 하강법으로 구한 수치(w1: 4.022, w0: 6.162)과 큰 차이가 없으며, 예측 오류 비용 또한 0.9937로 경사 하강법으로 구한 예측 오류 비용 0.9935 보다 아주 조금 높을 뿐 큰 예측 성능상의 차이가 없음을 알 수 있다.
따라서 큰 데이터를 처리할 경우에는 경사 하강법은 매우 시간이 오래 걸리므로 일반적으로 확률적 경사 하강법을 이용한다.
다음 내용
[머신러닝] 회귀 - LinearRegression 클래스
사이킷런 LinearRegression scikit-learn: machine learning in Python — scikit-learn 1.5.2 documentationComparing, validating and choosing parameters and models. Applications: Improved accuracy via parameter tuning. Algorithms: Grid search, cross v
puppy-foot-it.tistory.com
[출처]
파이썬 머신러닝 완벽 가이드 - 권철민 저, 위키북스
핸즈온 머신러닝 3판 - 오렐리앙 제롱 저, 한빛미디어
'[파이썬 Projects] > <파이썬 머신러닝>' 카테고리의 다른 글
| [머신러닝] 회귀 - 다항 회귀와 과대(과소) 적합 (3) | 2024.10.22 |
|---|---|
| [머신러닝] 회귀 - LinearRegression 클래스 (2) | 2024.10.21 |
| [머신러닝] 회귀(Regression) (2) | 2024.09.21 |
| [머신러닝] 스태킹 앙상블 (0) | 2024.09.21 |
| [머신러닝] Pytorch 설치하기 (Nvidia GPU 버전) (0) | 2024.09.09 |



