사이킷런 LinearRegression

scikit-learn: machine learning in Python — scikit-learn 1.5.2 documentation
Comparing, validating and choosing parameters and models. Applications: Improved accuracy via parameter tuning. Algorithms: Grid search, cross validation, metrics, and more...
scikit-learn.org
LinearRegression 클래스는 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화해 OLS(Ordinary Least Squares) 추정 방식으로 구현한 클래스이며, fit() 메서드로 X, y 배열을 입력받으면 회귀 계수(Coefficients)인 W(가중치)를 coef_속성에 저장한다.
OLS 기반의 회귀 계수 계산은 입력 피처의 독립성에 많은 영향을 받는다. 피처간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 매우 민감해지고, 이러한 현상을 다중 공선성(multi-collinearity) 문제라고 한다.
일반적으로 상관관계가 높은 피처가 많은 경우 독립적인 중요한 피처만 남기고 제거하거나 규제를 적용한다.
또한, 매우 많은 피처가 다중 공선성 문제를 가지고 있다면 PCA(주성분 분석)를 통해 차원 축소를 수행하는 것도 고려해 볼 수 있다.
class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)- fit_intercept: 불린 값으로, 디폴트는 True. intercept(절편) 값을 계산할 지 말지를 지정하며, False 로 지정하면 intercept가 사용되지 않고 0으로 지정됨.
- normalize: 불린 값으로 디폴트는 False. fit_intercept가 False인 경우에는 이 파라미터가 무시된다. True 이면 회귀를 수행하기 전에 입력 데이터 세트를 정규화.
- coef_: fit() 메서드를 수행했을 때 회귀 계수가 배열 형태로 저장하는 속성. Shape는 (Target 값 개수, 피처 개수)
- intercept_: intercept 값
회귀 평가 지표

과거 버전의 사이킷런은 RMSE를 제공하지 않아 RSME를 구하기 위해서는 MSE에 제곱근을 씌워서 계산하는 함수를 직접 만들어야 했지만, 0.22 버전부터는 RMSE를 위한 함수를 제공한다.

[각 평가 방법에 대한 사이킷런의 API 및 cross_val_score 나 GridSearchCV에서 평가 시 사용되는 scoring 파라미터 적용 값]
| 평가 방법 | 사이킷런 평가 지표 API | Scoring 함수 적용 값 |
| MAE | metrics.mean_absolute_error | 'neg_mean_absolute_error' |
| MSE | metrics.mean_squared_error | 'neg_mean_squared_error' |
| RMSE | metrics.mean_absolute_error를 그대로 사용하되, squared 파라미터를 False로 설정 | 'neg_root_mean_squared_error' |
| MSLE | metrics.mean_ squared_log_error | 'neg_mean_squared_log_error' |
| R^2 | metrics.r2_score | 'r2' |
※ 'neg'라는 접두어의 의미는 negative(음수) 값을 가진다는 의미이나, MAE는 절댓값의 합이기 대문에 음수가 될 수 없다.
LinearRegression을 이용해 보스턴 주택 가격 회귀 구현
사이킷런은 보스턴 주택 가격 데이터 세트를 load_boston()을 통해 제공해 왔으나, 윤리적인 문제로 삭제되었다.
사이킷런의 load_boston() 함수가 삭제될 예정입니다.
사이킷런의 load_boston() 함수가 삭제될 예정입니다. 이 데이터셋의 문제는 특성 “B” 때문입니다. 문서에서 볼 수 있듯이 이 특성은 도시의 흑인 비율을 사용합니다. 흑인 비율이 주택 가격에 미
tensorflow.blog
# 보스턴 주택 가격
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy import stats
from sklearn import datasets
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
# boston 데이터 세트 로드
X, y = datasets.fetch_openml('boston', return_X_y=True)
X.head()그러나 OpenML에서 제공하고 있어 데이터셋을 불러올 수는 있다.
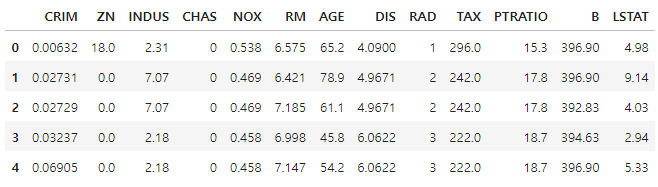
[해당 피처(각 칼럼)에 대한 설명]
- CRIM: 지역별 범죄 발생률
- ZN: 25,000 평방피트를 초과하는 거주 지역의 비율
- INDUS: 비상업 지역 넓이 비율
- CHAS: 찰스강에 대한 더미 변수(강의 경계에 위치한 경우는 1, 아니면 0)
- NOX: 일산화질소 농도
- RM: 거주할 수 있는 방 개수
- AGE: 1940년 이전에 건축된 소유 주택의 비율
- DIS: 5개 주요 고용센터까지의 가중 거리
- RAD: 고속도로 접근 용이도
- TAX: 10,000 달러당 재산세율
- PTRATIO: 지역의 교사와 학생 수 비율
- B: 지역의 흑인 거주 비율(해당 항목이 윤리적 문제 이슈가 있음)
- LSTAT: 하위 계층의 비율
- MEDV: 본인 소유의 주택 가격(중앙값)
데이터 세트 피처의 Null 값은 없으며 대부분이 float 형이다.
X.info()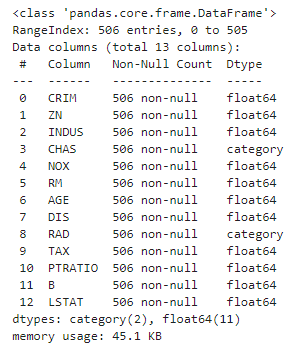
◆ 데이터 시각화
각 칼럼이 회귀 결과에 미치는 영향이 어느 정도인지 시각화해서 알아본다.
▶ 'B' 칼럼을 제외한 나머지 칼럼의 값이 증가할수록 PRICE 값이 어떻게 변하는지 확인한다.
시본(seaborn)의 regplot() 함수는 X, y 축 값의 산점도와 함께 선형 회귀 직선을 그려주며, matplotlib.subplots()를 이용해 각 ax 마다 칼럼과 PRICE의 관계를 표현한다.
※ matplotlib의 subplots() 은 여러 개의 그래프를 한 번에 표현하기 위해 자주 사용된다.
인자로 입력되는 ncols는 열 방향으로 위치할 그래프의 개수이며, nrows 는 행 방향으로 위치할 그래프의 개수이다.
# 보스턴 주택 가격
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy import stats
from sklearn import datasets
import warnings
warnings.filterwarnings('ignore')
# boston 데이터 세트 로드
boston = datasets.fetch_openml('boston', return_X_y=True, as_frame=True)
# boston 데이터 세트 DataFrame 변환
bostonDF = pd.DataFrame(boston[0], columns=boston[0].columns)
# Categorical 데이터 타입을 numeric 타입으로 변환 (필요한 경우)
for col in bostonDF.columns:
if pd.api.types.is_categorical_dtype(bostonDF[col]):
bostonDF[col] = bostonDF[col].astype(float)
# boston 데이터 세트의 target 배열은 주택 가격임. 이를 PRICE 칼럼으로 DF에 추가함.
bostonDF['PRICE'] = boston[1]
# 2개의 행과 4개의 열을 가진 subplots를 이용. axs는 4x2개의 ax를 가짐
fig, axs = plt.subplots(figsize=(16, 8), ncols=4, nrows=2)
lm_features = ['RM', 'ZN', 'INDUS', 'NOX', 'AGE', 'PTRATIO', 'LSTAT', 'RAD']
# subplot에 산점도와 선형 회귀 직선 그리기
for i, feature in enumerate(lm_features):
row = i // 4
col = i % 4
sns.regplot(x=feature, y='PRICE', data=bostonDF, ax=axs[row, col])
plt.tight_layout()
plt.show()
일부 코드를 수정하고, 'B' 칼럼을 제외한 나머지 칼럼의 값이 증가할수록 PRICE 값이 어떻게 변하는지 확인하기 위해 코드를 추가하였다.
- fetch_openml 함수에서 as_frame=True 옵션을 추가하여 데이터가 데이터프레임 형태로 로드되도록 수정.
- axs[row][col] 대신 axs[row, col]로 접근 방식을 변경
- 로드된 데이터의 일부 열이 Categorical 형식으로 되어 있기 때문에 문제가 발생하였다 (TypeError). Categorical 데이터는 기본적으로 순서가 없으며, 선형 회귀 분석이나 다른 수학적 계산에서 이러한 오류를 발생시킬 수 있있기 때문에 Categorical 열을 astype을 사용해 numeric 형식이나 float로 변환.
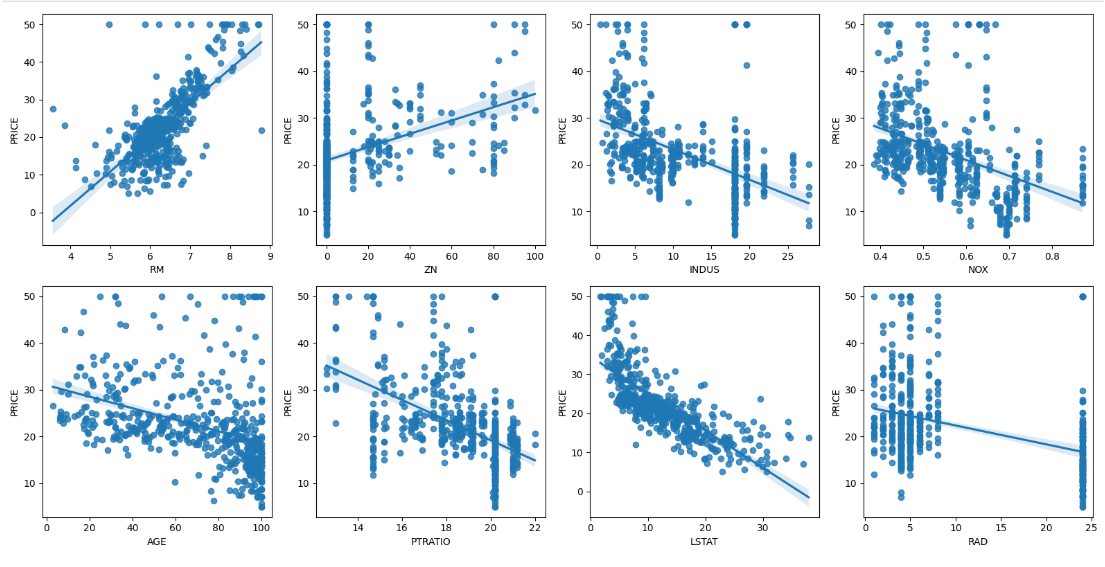
▶ 다른 칼럼보다 RM과 LSTAT의 PRICE 영향도가 가장 두드러지게 나타난다. RM(방 개수)은 양 방향의 선형성이 가장 큰데, 즉 방의 크기가 클수록 가격이 증가하는 것이 확연히 보인다.
또한, LSTAT(하위 계층의 비율)는 음 방향의 선형성이 가장 큰데, LSTAT이 적을 수록 PRICE가 증가하는 모습이 확연하게 나타난다.
◆ LinearRegression 클래스를 이용한 보스턴 주택 가격의 회귀 모델 만들기
train_test_split()을 이용해 학습과 테스트 데이터 세트를 분리해 학습과 예측 수행하고,
metrics 모듈의 mean_squared_error()와 r2_score() API를 이용해 MSE와 R2 Score를 측정
# 주택 가격의 회귀 모델
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'], axis=1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_data, y_target, test_size=0.3, random_state=156)
# 선형 회귀 OLS로 학습/예측/평가 수행
lr = LinearRegression()
lr.fit(X_train, y_train)
y_preds = lr.predict(X_test)
mse = mean_squared_error(y_test, y_preds)
rmse = np.sqrt(mse)
print('MSE : {0:.3f}, RMSE{1:.3f}'.format(mse, rmse))
print('Variance score: {0:.3f}'.format(r2_score(y_test, y_preds)))
[해당 주택가격 모델의 intercept(절편)과 coefficients(회귀 계수) 값 보기]
print('절편 값:', lr.intercept_)
print('회귀 계수값:', np.round(lr.coef_, 1))
coef_ 속성은 회귀 계수 값만 가지고 있으므로 이를 피처별 회귀 계수 값으로 다시 매핑하고, 높은 값 순으로 출력
: 판다스 Series의 sort_values() 함수 이용
# 회귀 계수를 큰 값 순으로 정렬
coeff = pd.Series(data=np.round(lr.coef_, 1), index = X_data.columns)
coeff.sort_values(ascending=False)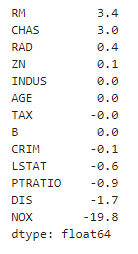
▶ RM이 양의 값으로 회귀 계수가 가장 크며, NOX 피처의 회귀 계수 - 값이 커 보인다.
[5개의 폴드 세트에서 cross_val_score()를 이용해 교차 검증으로 MSE와 RMSE 측정]
일반적으로 회귀는 MSE 값이 낮을수록 좋은 회귀 모델이다.
# 교차 검증으로 MSE, RMSE 측정
from sklearn.model_selection import cross_val_score
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'], axis=1, inplace=False)
lr = LinearRegression()
# cross_val_score()로 5 폴드 세트로 MSE를 구한 뒤 이를 기반으로 다시 RMSE 구함
neg_mse_scores = cross_val_score(lr, X_data, y_target, scoring = "neg_mean_squared_error", cv=5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
# cross_val_score(scoring="neg_mean_squared_error")로 반환된 값은 모두 음수
print('5 folds의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 2))
print('5 folds의 개별 RMSE scores: ', np.round(rmse_scores, 2))
print('5 folds의 평균 RMSE: {0:.3f}'.format(avg_rmse))
다음 내용
[머신러닝] 회귀 - 다항 회귀와 과대(과소) 적합
이전 내용 [머신러닝] 회귀 - LinearRegression 클래스사이킷런 LinearRegression scikit-learn: machine learning in Python — scikit-learn 1.5.2 documentationComparing, validating and choosing parameters and models. Applications: Improve
puppy-foot-it.tistory.com
[출처]
파이썬 머신러닝 완벽 가이드
사이킷런 공식 블로그
'[파이썬 Projects] > <파이썬 머신러닝>' 카테고리의 다른 글
| [머신러닝] 회귀 - 규제 선형 모델: 릿지, 라쏘, 엘라스틱넷 (1) | 2024.10.22 |
|---|---|
| [머신러닝] 회귀 - 다항 회귀와 과대(과소) 적합 (3) | 2024.10.22 |
| [머신러닝] 경사 하강법(GD, gradient descent) (3) | 2024.09.22 |
| [머신러닝] 회귀(Regression) (2) | 2024.09.21 |
| [머신러닝] 스태킹 앙상블 (0) | 2024.09.21 |



