로그
로그(logarithm)는 특정 수와 밑이 있을 때 거듭제곱 횟수를 구하는 수학 함수이다.
로그는 실제로 지진 측정, 스트레오 음량 관리 등 다양하게 사용되며, 어디에나 존재한다.
로그는 머신러닝과 데이터 과학에도 많이 사용되며, 특히 로지스틱 회귀의 핵심이다.
'2를 몇 번 제곱하면 8이 되는가?' 라는 질문을 수학적으로 표현하는 방법은 지수에 x를 사용하는 것이다.
이 수학 연산을 로그로 x를 구하는 식으로 표현한다면 아래와 같다.

로그는 밑이 2일 때 8이 되는 거듭제곱 횟수를 찾는다. 일반적으로 지수 함수를 로그로 표현하는 공식은 다음과 같다.

[파이썬에서 로그 계산하는 방식]
# 파이썬에서 로그 계산하기
from math import log
#2를 거듭제곱해 8이 되는 지수를 구하라
x = log(8, 2)
print(x)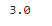
▶ 파이썬에서 log() 함수에 밑 인수를 제공하지 않으면 일반적으로 기본 밑이 제공된다.
데이터 과학에서 로그의 기본 밑은 오일러 수(е) 를 사용한다.
지수와 마찬가지로 로그도 곱셈, 나눗셈, 거듭제곱 등과 관련된 몇 가지 속성을 가진다.

오일러 수(e)
오일러의 수는 자연로그의 밑수로서 파이(π) 와 비슷한 특수한 숫자이며, 중요한 상수이다. 그 값은 약 2.7183이다.
e를 사용하면 수학적으로 여러 문제를 단순화할 수 있어 이를 많이 사용한다.
오일러 수가 밑인 지수 함수의 도함수가 자기 자신이라는 점이 오일러 수의 특성이다.
밑이 중요하지 않은 많은 애플리케이션에서는 가장 간단한 도함수를 만드는 오일러 수를 선택하는데, 이것이 많은 데이터 과학 함수에서 오일러 수를 기본 밑으로 사용하는 이유이다.
★ 도함수: x의 함수로 본 것을 도함수라고 하고 f'(x)로 나타낸다. 접선의 기울기를 구하고자 할 때 많이 사용한다.
◆ 복리 이자를 계산하는 방법을 통한 오일러 수를 설명
누군가에게 연 10%의 이자로 500만원을 빌려준다고 가정하고,
이자는 월 복리로 계산되기 때문에 매달 이자는 0.10/12= 0.00833%가 된다.
그렇다면 2년 후 대출 잔액은 얼마가 될까? (중도 상환 없이)
이자 계산 공식은
시작 투자금 P에 대한 잔액 A, 이자율 r, 기간(연도 수) t, 연간 복리 적용 횟수n 으로 구성된다.

이를 파이썬에서 수행하려면 아래와 같이 코드를 입력하면 된다.
▶ 일반적으로 exp() 함수를 사용하는 파이썬, 엑셀과 같은 플랫폼에서는 e를 지수의 밑으로 사용한다. e는 매우 널리 사용되며 지수와 로그 함수의 기본 밑이다.
# 복리 이자 계산하기
from math import exp
p = 5000000 # 시작 투자금
r = 0.10 # 이자율
t = 2.0 # 기간: 2년
n = 12 # 연간 복리 적용횟수
a = p * (1 + (r/n))**(n * t)
print(a)
매월 복리 이자를 적용하면 대출금이 6,101,954.8원으로 늘어나게 된다.

만약 기간을 매월이 아닌 매일(365)로 계산한다면,
# 복리 이자 계산하기(매일)
from math import exp
p = 5000000 # 시작 투자금
r = 0.10 # 이자율
t = 2.0 # 기간: 2년
n = 365 # 연간 복리 적용횟수
a = p * (1 + (r/n))**(n * t)
print(a)

6,106,846.5 원으로 월단위로 할 때보다 약 4,892원을 더 벌 수 있다.
만약 이를 매시간 (8,760) 복리로 바꾼다면?
# 복리 이자 계산하기(매시간)
from math import exp
p = 5000000 # 시작 투자금
r = 0.10 # 이자율
t = 2.0 # 기간: 2년
n = 8760 # 연간 복리 적용횟수
a = p * (1 + (r/n))**(n * t)
print(a)약 6,107,006.8 원으로 일복리를 적용할 때 보다 약 160원을 더 벌 수 있다.

복리를 더 자주 할수록 점점 더 작은 금액의 이득을 얻고 있다. 그렇다면 이 기간을 무한히 작게 만들어 계속 복리를 하게 된다면?
다음은 쉬지 않고 복리를 적용하는 공식이다.

오일러 수는 약 2.71828 이므로, 이를 대입하여 연속적으로 복리를 적용했을 때 2년 후 대출 잔액을 계산해본다.
# 연속 이자 계산하기
from math import exp
p = 5000000 # 시작 투자금
r = 0.10 # 이자율
t = 2.0 # 기간: 2년
a = p * exp(r*t)
print(a)연속해서 복리를 적용하면 6,107,013.79 원이라는 값에 매우 근접하게 된다.

◆ 복리 이자 공식과 연속 이자 공식은 구조적으로는 비슷해 보이나 차이가 있다.

e는 n이 점점 커져 무한대에 가까워졌을 때 (1+1/n)^n 의 결괏값이다.
n이 커질수록 증가율이 감소하고 약 2.71828에 수렴하는데, 이 값이 e다.
e가 모집단 증가를 연구하는 데에만 사용되는 것은 아니며 수학의 많은 영역에서 핵심적인 역할을 하고 있다.
자연로그
e를 로그의 밑으로 사용할 때 이를 자연로그(natural logarithm) 라고 부른다. 플랫폼에 따라 자연로그를 지정하는 데 log() 대신 ln()을 사용할 수 있다. 따라서 e를 거듭제곱해 10이 되는 지수를 찾는다는 의미의 자연로그를 아래와 같이 줄여서 표현하기도 한다.

파이썬에서는 log() 함수가 자연로그이다. 밑을 지정하는 두 번째 매개변수를 별도로 지정하지 않으면 기본값 e를 사용한다.
# 10의 자연로그 계산하기
from math import log
# e를 거듭제곱해 10이 되는 지수는?
x = log(10)
print(x)
극한
입력 변수를 계속 증가하거나 감소할 때 출력 변수가 특정한 값에 계속 근접하지만, 그 값에는 도달하지 못하는 경우가 있다.
예를 들어 아래와 같은 함수가 있다고 하면,

x가 증가함에 따라 f(x)가 0에 실제로 도달하지 못하고 가까워지만 진다.
따라서, 이 함수의 운명은 x가 무한대가 됨에 따라 0에 계속 가까워지지만, 결코 0에 도달하지는 못한다.
극한:
영원히 가까워지지만 결코 도달하지 못하는 값을 표현하는 방법

이를 읽는 방법은 'x가 무한대에 가까워짐에 따라 함수 1/x 는 0에 가까워지지만, 결코 0에 도달하지는 않는다.' 이다.
이는 특히 미분과 적분을 공부할 때 이런 종류의 형태를 많이 볼 수 있다.
파이썬에서는 심파이를 사용하면 x가 무한대에 가까워질 때 f(x)=1/x 이 어떤 값에 접근하는지를 계산할 수 있다.
(심파이에서 무한대는 oo 으로 나타낸다)
# 심파이로 극한 계산하기
from sympy import *
x = symbols('x')
f = 1/x
result = limit(f, x, oo)
print(result)
★ 심파이에서 극한으로 오일러 수를 계산하면 심파이는 이를 오일러 수로 즉시 인식한다. 그러나 evalf()를 호출하면 실제 숫자를 표시한다.
# 극한으로 오일러 수 입력해보기
from sympy import *
n = symbols('n')
f = (1 + (1/n))**n
result = limit(f, n, oo)
print(result)
print(result.evalf())
[출처]
개발자를 위한 필수 수학
네이버 지식백과
위키백과
나무 위키
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [통계학] 자료 정리 - 2 (1) | 2024.10.03 |
|---|---|
| [통계학] 자료 정리 - 1 (4) | 2024.10.02 |
| [개발자를 위한 수학] 미분, 적분 (+파이썬) (5) | 2024.10.02 |
| [개발자를 위한 수학] 기초수학 (+파이썬) (0) | 2024.10.02 |
| [통계학] 통계학의 기초개념 (0) | 2024.05.02 |


