★ 시작에 앞서 ★
해당 내용은 '<현대통계학-제6판>, 다산출판사, 2024' 에 나와있는 챕터별 연습문제를 교재를 응용하여 풀이하고, 수학적인 문제에 대한 답변을 파이썬으로 구현해보기 위해 작성하는 글이다.
해당 답변을 구현하는 방식은 답안지 없이 필자가 스스로 구현하는 것이므로, 정확한 (혹은 가장 효과적인) 답변이 아닐 수 있다. 이 글의 목적은 통계학 공부와 파이썬 프로그래밍 언어 공부를 동시에 하고자 함이며, 통계학을 공부하고 싶으신 분들은 해당 교재를 구매하는 것을 추천한다.
또한, 연습문제 번호 및 문제 내용은 필자가 임의대로 작성하였으며, 교재와는 다를 수 있다.
잘못된 부분이 있다면 언제든 피드백 부탁 드립니다! 감사합니다
이전 내용
[파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.4)
★ 시작에 앞서 ★ 해당 내용은 ', 다산출판사, 2024' 에 나와있는 챕터별 연습문제를 교재를 응용하여 풀이하고, 수학적인 문제에 대한 답변을 파이썬으로 구현해보기 위해 작성하는 글이다.해
puppy-foot-it.tistory.com
챕터4 주요 개념: 확률, 집합이론, 독립사건과 종속사건, 베이즈정리
챕터4 연습문제6
Q. 어느 도시의 날씨가 맑을 확률이 60%, 흐릴 확률이 30%, 비가 올 확률이 10%라고 하자. 이 도시에 살고 있는 학생 김 군은 맑은 날 지각할 확률이 10%, 흐린 날 지각할 확률이 25%, 비오는 날 지각할 확률이 40% 라고 한다.
어느날 김 군이 지각을 했는데, 그날 날씨가 흐렸을 확률은?

def bayes_theorem(P_A_B, P_B, P_A_C, P_C, P_A_A, P_A):
# P_B_A = 흐린 날에 지각할 확률
P_B_A = (P_A_B * P_B) / (P_A_B * P_B + P_A_A * P_A + P_A_C * P_C)
return P_B_A
# 날씨 확률
P_A = 0.6 # 맑은 날
P_B = 0.3 # 흐린 날
P_C = 0.1 # 비오는 날
# 지각할 확률
P_A_A = 0.1 # 맑은 날에 지각할 확률
P_A_B = 0.25 # 흐린 날에 지각할 확률
P_A_C = 0.4 # 비오는 날에 지각할 확률
# 지각했는데 흐린 날일 확률
w_and_late_cloudy = bayes_theorem(P_A_B, P_B, P_A_C, P_C, P_A_A, P_A)
print(f"지각한 날이 흐린 날일 확률: {w_and_late_cloudy:.4f}")
챕터4 연습문제 7
Q. 202X년 전국동시지방선거 출구조사를 위해 어느 도시의 A,B, C 세 개의 투표소에서 출구조사를 진행하였다. 이들 투표소의 출구조사에서 전체 응답자 중 거짓응답자의 비율이 각각 5%, 3%, 2%고, A, B, C 세 투표소의 투표자 수는 이 도시 전체 인구의 20%, 30%, 50%를 차지한다.
한 명의 투표자를 임의로 선택하였을 때, 그 응답자가 거짓응답자였다면 그 사람이 B 투표소에서 투표한 사람이었을 확률은?
(이 도시 전체 유권자의 투표율은 100%이고, 모든 투표자가 출구 조사에 응답했다고 가정)

# 투표 출구조사
def bayes_theorem(P_V_B, P_B, P_V_C, P_C, P_V_A, P_A):
# P_B_V = 거짓응답자가 B 투표소에서 투표했을 확률
P_B_V = (P_V_B * P_B) / (P_V_B * P_B + P_V_A * P_A + P_V_C * P_C)
return P_B_V
# 거짓응답자 비율
P_A = 0.05
P_B = 0.03
P_C = 0.02
# 투표자 비율
P_V_A = 0.2
P_V_B = 0.3
P_V_C = 0.5
# 거짓응답자가 B 투표소에서 투표했을 확률
liar_V_B = bayes_theorem(P_V_B, P_B, P_V_C, P_C, P_V_A, P_A)
print(f"거짓응답자가 B 투표소에서 투표했을 확률: {liar_V_B: .4f}")
집합 이론
집합(set)이란, 개체 또는 원소(element)의 모임이라고 정의된다.
원소: 집합을 형성하는 개별 사물, 개별 사물은 명확히 정의 되어야 한다. 또한, 원소는 { } 속에 넣는 것이 관례이다.
예. 짱구네 집 = {신형만, 봉미선, 신짱구, 신짱아, 흰둥이}
이때, 짱구 집 각 식구들을 원소라고 부른다.
특정한 문제에서 가능한 모든 원소의 집합을 전체집합(universal set) 이라고 하며, 이 모든 원소 중 일부를 나타내는 집합을 부분 집합이라고 한다.
[짱구네 식구 전체 집합]
짱구네 집 = {신형만, 봉미선, 신짱구, 신짱아, 흰둥이}
[짱구네 식구 부분 집합]
짱구네 아기들 = {신짱구, 신짱아}
집합연산에는 여러 가지가 있는데, 그 중 여집합(complementary sets), 합집합(union of sets), 교집합(intersection of sets)에 대해 알아보자.
◆ 여집합
전체 집합과 관심이 되는 부분집합 A가 정의되면 전체집합 중에서 집합 A에 포함되지 않는 부분이 생기는데, 이를 집합 A의 여집합이라고 한다.
앞서, 짱구네 식구 전체 집합 중, 짱구네 아기들(부분집합 A)을 제외한 부분이 여집합이 된다.
즉,
부분집합 A의 여집합 = {신형만, 봉미선, 흰둥이}

◆ 합집합
두 개의 집합 A와 B의 합집합은 집합 A 또는 집합 B에 속하는 원소들로 구성된 집합을 말한다.
즉, 집합 A나 B 중에서 하나의 집합에 속하거나, 두 집합 모두에 속하는 원소들로 구성된 집합을 말하며,
A∪B 로 나타낸다.
부분집합 A = {신짱구, 신짱아}
부분집합 B = {신짱구, 철수, 맹구, 훈이, 유리, 수지}
라고 했을 때, A∪B의 벤 다이어그램은 아래와 같다.
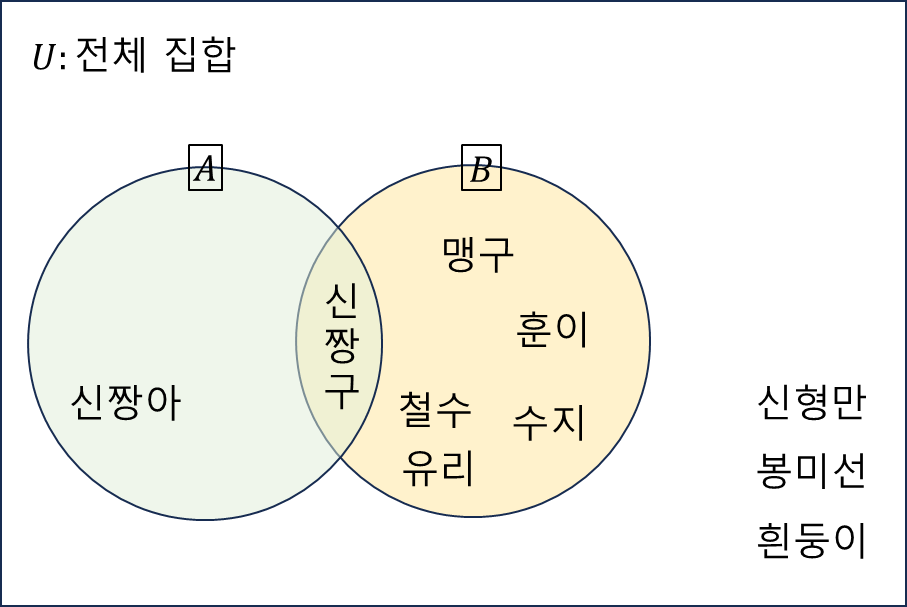
◆ 교집합
두 개의 집합 A와 B의 교집합은 A∩B 로 표시되는데, 집합 A와 B에 공통적으로 속해 있는 원소만을 포함하는 집합이다.
즉, 위의 벤 다이어그램을 예로 들면
A∩B = {신짱구}
가 된다.

◆ 합집합의 계산
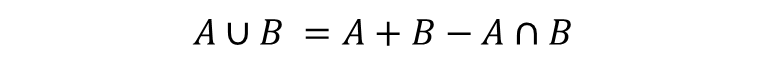
만약, 전체집합 U, 부분집합 A, 부분집합 B가 아래와 같다면
U = {1, 2, 3,... 8, 9, 10}
A = {1, 2, 3}
B = {3, 4, 5}
A∩B = {3}
A∪B 의 경우, {1, 2, 3} + {3, 4, 5} 로 {3}이 두 번 계산된다. 그런데 이 3은 집합 A와 집합 B의 교집합이므로,
A∪B = {1, 2, 3} + {3, 4, 5} - {3} = {1, 2, 3, 4, 5} 가 된다.
◆ 공집합
그러나 집합 A와 집합 B에서 두 집합의 공통원소가 하나도 없는 특수한 경우가 있을 수 있다.
예를 들어, 부분집합 C = {6, 7, 8, 9} 일 때는 A∩C에 해당되는 원소가 하나도 없다.
이와 같이 원소가 하나도 없는 텅빈 집합을 공집합(empty sets)이라고 하며, ∅ 으로 나타낸다.
A∩C = ∅
이렇듯 두 집합이 공통으로 소유하는 원소가 없는 경우는 두 집합이 서로 배타적(mutually exclusive) 이라고 한다.
배타적 집합일 경우의 합집합 계산
A∪B = A + B
다음 내용
[파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.5)
★ 시작에 앞서 ★ 해당 내용은 ', 다산출판사, 2024' 에 나와있는 챕터별 연습문제를 교재를 응용하여 풀이하고, 수학적인 문제에 대한 답변을 파이썬으로 구현해보기 위해 작성하는 글이다.해
puppy-foot-it.tistory.com
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.6)-1 (5) | 2024.10.10 |
|---|---|
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.5) (2) | 2024.10.10 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.4) -1 (0) | 2024.10.08 |
| [개발자를 위한 수학] 선형대수학: 고유 벡터와 고윳값 (2) | 2024.10.07 |
| [개발자를 위한 수학] 선형대수학: 연립 방정식과 역행렬 (0) | 2024.10.07 |



