머신러닝 기반 분석 모형 선정
[머신러닝] 머신러닝 기반 분석 모형 선정
머신러닝 기반 분석 모형 선정 지도 학습, 비지도 학습, 강화 학습, 준지도 학습, 전이 학습 1) 지도 학습: 정답인 레이블(Label)이 포함되어 있는 학습 데이터를 통해 컴퓨터를 학습시키는 방법(
puppy-foot-it.tistory.com
인공 신경망
[딥러닝] 인공 신경망(ANN)
머신러닝 기반 분석 모형 선정 [머신러닝] 머신러닝 기반 분석 모형 선정머신러닝 기반 분석 모형 선정 지도 학습, 비지도 학습, 강화 학습, 준지도 학습, 전이 학습 1) 지도 학습: 정답인 레
puppy-foot-it.tistory.com
퍼셉트론(perceptron)
퍼셉트론은 가장 간단한 인공 신경망 구조로, TLU 또는 LTU 라고 불리는 조금 다른 형태의 인공 뉴런을 기반으로 한다. 입력과 출력이 이진값이 아닌 어떤 숫자이고, 각각의 입력 연결은 가중치와 연관되어 있다. TLU는 먼저 입력의 선형 함수를 계산하고, 이 결과에 계단 함수를 적용한다.
로지스틱 회귀와 거의 비슷하지만 로지스틱 함수 대신 스텝 함수를 사용한다는 점이 다르나, 모델 파라미터는 로지스틱 회귀와 동일한 입력 가중치w와 편향b이다.
퍼셉트론에서 가장 널리 사용되는 계단 함수는 헤비사이드 계단 함수이며, 이따금 부호 함수를 대신 사용하기도 한다.
하나의 TLU는 간단한 선형 이진 분류 문제에 사용될 수 있다. 입력의 선형 함수를 계산해서 그 결과가 임곗값을 넘으면 양성 클래스를 출력하고, 그렇지 않으면 음성 클래스를 출력한다.
퍼셉트론은 하나의 층 안에 놓인 하나 이상의 TLU로 구성되며, 각각의 TLU는 모든 입력에 연결되는데, 이러한 층을 완전 연결 층 또는 밀집 층이라고 하며, 입력은 입력 층을 구성한다. 그리고 TLU의 층이 최종 출력을 생성하기 때문에 이를 출력 층이라고 한다.
예를 들어 두 개의 입력(Input layer)과 세 개의 출력(Output layer) 으로 구성된 퍼셉트론의 구조는 아래와 같다.

▶ 이 퍼셉트론은 샘플을 세 개의 이진 클래스로 동시에 분류할 수 있으므로 다중 레이블 분류기이며, 다중 분류에도 사용할 수 있다.
퍼셉트론은 네트워크가 예측할 때 만드는 오차를 반영하도록 조금 변형된 규칙을 사용하여 훈련되며, 퍼셉트론 학습 규칙은 오차가 감소되도록 연결을 강화시킨다. 퍼셉트론은 한 번에 한 개의 샘플이 주입되면 각 샘플에 대해 예측이 만들어지는데, 잘못된 예측을 하는 모든 출력 뉴런에 대해 올바른 예측을 만들 수 있도록 입력에 연결된 가중치를 강화시킨다.
각 출력 뉴런의 결정 경계는 선형이므로 퍼셉트론도 로지스틱 회귀 분류기처럼 복잡한 패턴을 학습하지 못한다.
사이킷런에서의 퍼셉트론
사이킷런은 Perceptron 클래스를 제공하며, 파이썬 클래스도 동일한 방식으로 사용된다.
사이킷런의 Perceptron 클래스는 매개변수가 loss='perceptron', learning_rate='constant', eta0=1(학습률), penalty=None (규제 없음)인 SGDClassifier와 같다.
붓꽃 데이터셋을 이용한 퍼셉트론 예제
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris(as_frame=True)
X = iris.data[['petal length (cm)', 'petal width (cm)']].values
y = (iris.target == 0) # iris-setosa
per_clf = Perceptron(random_state=42)
per_clf.fit(X, y)
X_new = [[2, 0.5], [3, 1]]
y_pred = per_clf.predict(X_new) # 두 꽃에 대한 예측은 True / False
y_pred
퍼셉트론은 배타적 논리합(XOR) 분류 문제 등 간단한 문제를 풀 수 없다.
로지스틱 회귀 분류기와 달리 퍼셉트론은 클래스 확률을 출력하지 않아 퍼셉트론보다 로지스틱을 선호한다. 또한 퍼셉트론은 기본적으로 정규화를 사용하지 않으며, 훈련 세트에 더 이상 예측 오차가 없으면 훈련을 중단한다. 따라서 일반적으로 로지스틱 회귀나 선형 SVM 분류기만큼 일반화가 잘 되지 않는다.
하지만 퍼셉트론을 조금 더 빠르게 훈련할 수 있다.
다층 퍼셉트론(multi layer perceptron, MLP)
퍼셉트론을 여러 개 쌓아올린 것으로, 퍼셉트론을 여러 개 쌓아올리면 일부 제약을 줄일 수 있고 XOR 문제를 풀 수 있다는 것이 밝혀졌다.
다층 퍼셉트론은 입력 층 하나와 은닉 층(hidden layer)이라 불리는 하나 이상의 TLU 층과 마지막 출력 층으로 구성된다. 입력 층과 가까운 층을 하위 층(lower layer)이라 부르고 출력에 가까운 층을 상위 층(upper layer)이라 부른다.
두 개의 입력, 네 개의 뉴런을 가진 은닉 층, 세 개의 출력 뉴런으로 구성된 다층 퍼셉트론의 구조는 아래와 같다.

▶ 신호는 입력에서 출력으로 한 방향으로만 흘러서 이 구조는 피드포워드 신경망(FNN)에 속한다.
은닉 층을 여러 개 쌓아 올린 인공 신경망을 심층 신경망(deep neural network, DNN) 이라고 하며, 딥러닝은 심층 신경망을 연구하는 분야이며 일반적으로는 연산이 연속하여 길게 연결된 모델을 연구한다.
◆ 역전파
수년 동안 연구자들은 MLP를 훈련하는 방법을 찾기 위해 고군분투 했지만 성공하지 못하다가, 1970년 한 연구원이 논문에서 모든 그레이디언트를 자동으로 효율적으로 계산하는 후진 모드 자동 미분 기법을 소개했다. 이 알고리즘은 네트워크를 두 번만 통과(전진, 후진) 하면 모든 단일 모델 파라미터에 대한 신경망 오차의 그레이디언트를 계산할 수 있다. 즉, 신경망의 오차를 줄이기 위해 각 연결 가중치와 편향을 어떻게 조정해야 하는지 알아낼 수 있다.
그리고 이 그레이디언트를 사용하여 경사 하강법 단계를 수행하는 데, 그레이디언트를 자동으로 계산하고 경사 하강법 단계를 수행하는 과정을 반복하면 신경망의 오차가 점차 감소하여 결국 최솟값에 도달하게 된다.
이러한 후진 모드 자동 미분과 경사 하강법을 결합한 것을 역전파(backpropagation) 라고 한다.
[역전파의 작동 방식]
- 한 번에 하나의 미니배치씩 진행하여 전체 훈련 세트를 처리하고, 이 과정을 여러 번 반복 (에포크: 각 반복)
- 각 미니배치는 입력 층을 통해 네트워크로 들어감
- 알고리즘은 미니배치에 있는 모든 샘플에 대해 첫 번째 은닉 층에 있는 모든 뉴런의 출력 계산
- 계산 결과는 다음 층으로 전달하고, 다시 이 층의 출력을 계산하고 결과는 다음 층으로 전달
- 마지막 층인 출력 층의 출력을 계산할 때까지 지속
▶ 역방향 계산을 위해서는 중간 계산값을 모두 저장하는 것이 추가되며, 나머지는 동일
- 알고리즘의 네트워크의 출력 오차 측정 (손실 함수를 사용하여 기대하는 출력과 네트워크의 실제 출력을 비교하고 오차 측정값 반환)
- 각 출력의 오차와 출력 층의 각 연결이 이 오차에 얼마나 기여했는지 계산 (연쇄 법칙을 적용하면 빠르게 정확하게 수행)
- 다시 연쇄 법칙을 사용하여 이전 층의 연결 가중치가 이 오차의 기여 정도에 얼마나 기여했는지 측정
- 입력 층에 도달할 때까지 역방향으로 측정 계속 됨.
- 마지막으로 알고리즘은 경사 하강법을 수행하여 방금 계산한 오차 그레이디언트를 사용해 네트워크에 있는 모든 연결 가중치를 수정

계단 함수에는 수평선밖에 없어 그레이디언트가 없기 때문에, 이 알고리즘을 작동시키고자 계단 함수를 로지스틱 함수(시그모이드 함수)로 바꿨다. 시그모이드 함수는 어디서든지 0이 아닌 그레이디언트가 잘 정의되어 있다.
또한, 역전파 알고리즘은 시그모이드 함수 뿐만 아니라 tanh 함수(하이퍼볼릭 탄젠트 함수), ReLU 함수 같은 활성화 함수와도 사용할 수 있다.
회귀를 위한 다층 퍼셉트론
다층 퍼셉트론은 회귀 작업에 사용될 수 있는데,
- 여러 특성으로 값 하나 예측: 출력 뉴런은 하나만 필요하며, 이 뉴런의 출력이 예측된 값이다.
- 동시에 여러 값을 예측하는 다변량 회귀: 출력 차원마다 출력 뉴런이 하나씩 필요
◆ 사이킷런에서의 회귀를 위한 다층 퍼셉트론
사이킷런에는 MLPRegressor 클래스가 포함되어 있으므로 이를 사용해본다.
이 클래스를 사용하여 각각 50개의 뉴런을 가진 3개의 은닉 층으로만 구성된 MLP를 만들고 캘리포니아 주택 데이터셋에 훈련시켜본다.
사이킷런의 fetch_california_housing() 함수를 사용하여 데이터셋을 로드하면, 이 데이터셋은 숫자 특성만 포함하고 누락된 값이 없기 때문에 간단하다.
<대략적인 순서>
1. 데이터 로드
2. 데이터 분할(훈련, 테스트)
3. MLPRegressor로 전달할 입력 특성을 표준화하기 위한 파이프라인 생성
4. 모델 훈련 및 검증 오차 평가
▶ 은닉 층에 ReLU 활성화 함수를 사용하며, 평균 제곱 오차를 최소화하기 위해 Adam 이라는 변형된 경사 하강법을 사용하고 약간의 l2 정규화(alpha 하이퍼파라미터를 통해 제어) 적용
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full, random_state=42)
mlp_reg = MLPRegressor(hidden_layer_sizes=[50, 50, 50], random_state=42)
pipeline = make_pipeline(StandardScaler(), mlp_reg)
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_valid)
rmse = mean_squared_error(y_valid, y_pred, squared=False)
print(y_pred)
print(rmse)
이 MLP는 출력 층에 활성화 함수를 사용하지 않으므로 원하는 값을 자유롭게 출력할 수 있다.
- 출력이 항상 양수임을 보장하려면 출력 층에 ReLU 활성화 함수를 사용하거나 ReLU 의 부드러운 변형인 소프트플러스 함수를 사용해야 한다.
- 예측이 항상 주어진 값의 범위 내에 속하도록 보장하려면 시그모이드 함수 도는 쌍곡 탄젠트를 사용하고 적절한 범위로 타깃의 스케일을 조정해야 한다. (시그모이드 0~1, 탄젠트 -1~1 사이 출력)
그러나 MLPRegressor 클래스는 출력 층에서 활성화 함수를 지원하지 않는다.
MLPRegressor 클래스는 일반적으로 회귀에 필요한 평균 제곱 오차를 사용하지만, 훈련 세트에 이상치가 많은 경우 평균 절대 오차를 대신 사용하거나, 이 두 가지를 조합한 후버 손실을 사용하는 것이 더 좋을 수 있다.
선형 함수 부분은 평균 제곱 오차보다 이상치에 덜 민감하고, 이차 함수 부분은 평균 절대 오차보다 더 빠르고 정확하게 수렴하도록 도와준다. 그러나 MLPRegressor 클래스는 MSE만 지원한다.
| 하이퍼파라미터 | 일반적인 값 |
| 은닉 층 수 | 문제에 따라 다르나, 일반적으로 1~5 |
| 은닉 층의 뉴런 수 | 문제에 따라 다르나, 일반적으로 10~100 |
| 출력 뉴런 수 | 예측 차원마다 하나 |
| 은닉 층의 활성화 함수 | ReLU |
| 출력 층의 활성화 함수 | 없거나, 아래 두 가지 - 출력이 양수일 때: ReLU/소프트플러스 - 출력을 특정 범위로 제한할 때: 로지스틱/탄젠트 |
| 손실 함수 | MSE / 이상치가 있을 경우: 후버 |
분류를 위한 다층 퍼셉트론
다층 퍼셉트론은 분류 작업에도 사용된다.
이진 분류 문제에서는 시그모이드 활성화 함수를 가진 하나의 출력 뉴런만 필요하다. 출력은 0과 1 사이의 실수이며, 이를 양성 클래스에 대한 예측 확률로 해석할 수 있다.
음성 클래스에 대한 예측 확률은 1에서 양성 클래스의 예측 확률을 뺀 값이다.
| 하이퍼파라미터 | 이진 분류 | 다중 레이블 분류 | 다중 분류 |
| 은닉 층 수 | 문제에 따라 다르나, 일반적으로 1~5 | ||
| 출력 뉴런 수 | 1개 | 이진 레이블마다 1개 | 클래스마다 1개 |
| 출력 층의 활성화 함수 | 시그모이드 함수 | 시그모이드 함수 | 소프트맥스 함수 |
| 손실 함수 | 크로스 엔트로피 | 크로스 엔트로피 | 크로스 엔트로피 |
다중 퍼셉트론은 다중 레이블 이진 분류 문제를 쉽게 처리할 수 있다.
[이메일 분류 시스템의 예]
예를 들어 이메일이 스팸 메일인지 아닌지 예측하고 동시에 긴급한 메일인지 아닌지 예측하는 이메일 시스템이 있다고 가정하면, 이 경우 시그모이드 활성화 함수를 가진 두 출력 뉴런이 필요하다.
- A 뉴런: 이메일이 스팸일 확률 출력
- B 뉴런: 긴급한 메일일 확률 출력
- 출력될 확률의 합이 1일 필요는 없음.
모델은 어떤 레이블 조합도 출력할 수 있다.
- 긴급하지 않은 메일
- 긴급한 메일
- 긴급하지 않은 스팸 메일
- 긴급한 스팸 메일 등 (오류)
각 샘플이 3개 이상의 클래스 중 한 클래스에만 속할 수 있는 다중 분류라면 클래스마다 하나의 출력 뉴런이 필요하며, 출력 층에는 소프트맥스 활성화 함수를 사용해야 한다. 소프트맥스 함수는 모든 예측 확률을 0과 1 사이로 만들고 클래스가 서로 배타적이기 때문에 더했을 때 1이 된다.
확률 분포를 예측해야 하므로 손실 함수에는 일반적으로 크로스 엔트로피 손실(로그 손실)을 선택하는 것이 좋다.
◆ 사이킷런에서의 분류를 위한 다층 퍼셉트론
사이킷런은 sklearn.neural_network 패키지 아래 MLPClassifier 클래스를 제공한다.
이 클래스는 MLPRegressor 클래스와 거의 동일하지만 MSE가 아닌 크로스 엔트로피를 최소화한다는 점이 다르다.
MLPClassifier 클래스를 활용한 붓꽃데이터셋 분류 코드 (크로스 엔트로피 최소화)
from sklearn.metrics import log_loss
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.datasets import load_iris
# 1. 데이터 로드 및 분할
iris = load_iris()
X = iris['data']
y = iris['target']
# 훈련 및 테스트 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
# 2. 모델 생성 및 학습
mlp_clf = MLPClassifier(hidden_layer_sizes=[10, 10], random_state=42, max_iter=500)
pipeline = make_pipeline(StandardScaler(), mlp_clf)
pipeline.fit(X_train, y_train)
# 3. 확률 예측값 생성
y_proba = pipeline.predict_proba(X_test)
# 4. 크로스 엔트로피 계산
cross_entropy_loss = log_loss(y_test, y_proba)
print(f"Cross-Entropy Loss: {cross_entropy_loss:.4f}")
- log_loss 함수: log_loss는 크로스 엔트로피 손실 함수를 계산하는 함수. 인자로 y_test(실제 레이블)와 y_proba(모델이 예측한 확률값)를 받는다.
- predict_proba 메서드: MLPClassifier는 클래스별 확률값을 반환하는 predict_proba 메서드를 제공. 이 확률값은 크로스 엔트로피 계산에 필요.
- 출력값: 크로스 엔트로피 손실 값은 숫자로 출력되며, 값이 낮을수록 모델의 예측 성능이 더 좋음을 나타냄.
MLPClassifier 클래스를 활용한 붓꽃데이터셋 분류기 모델 성능 평가
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPClassifier
from sklearn.pipeline import make_pipeline
from sklearn.metrics import classification_report
# 1. 데이터 로드
iris = load_iris(as_frame=True)
X = iris['data']
y = iris['target']
# 2. 데이터 분할 (Train/Test)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
# 3. 모델 생성 (전처리 포함)
mlp_clf = MLPClassifier(hidden_layer_sizes=[10, 10, 10], random_state=42)
pipeline = make_pipeline(StandardScaler(), mlp_clf)
# 4. 모델 학습
pipeline.fit(X_train, y_train)
# 5. 예측 및 결과 평가
y_pred = pipeline.predict(X_test)
print(classification_report(y_test, y_pred))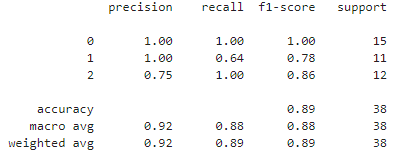
▶ Classification_report(분류 리포트) 모듈에서는 Precision(정확률), Recall(재현률), f1-score를 계산해준다.
붓꽃 데이터는 상대적으로 단순한 데이터 세트이므로 높은 정확도(90% 이상)가 나올 가능성이 높다.
[보완 및 개선]
1. 학습률 및 반복 횟수 조정
MLPClassifier는 비선형 데이터에서 잘 동작하지만, 하이퍼파라미터를 조정하면 성능을 더 개선할 수 있다.
# 하이퍼 파라미터 보완
mlp_clf = MLPClassifier(hidden_layer_sizes=[10, 10, 10], random_state=42, max_iter=500, learning_rate_init=0.01)
pipeline = make_pipeline(StandardScaler(), mlp_clf)
# 4. 모델 학습
pipeline.fit(X_train, y_train)
# 5. 예측 및 결과 평가
y_pred = pipeline.predict(X_test)
print(classification_report(y_test, y_pred))
▶ 정확도가 97%로 크게 개선되었다.
2. 교차 검증
학습/테스트 데이터 분할 외에도 교차 검증을 활용하면 모델 성능을 더 신뢰할 수 있다:
from sklearn.model_selection import cross_val_score
scores = cross_val_score(pipeline, X, y, cv=5)
print("교차 검증 점수:", scores)
3. 혼동 행렬(Confusion Matrix 시각화)
결과를 더 잘 이해할 수 있도록 ConfusionMatrixDisplay를 통해 혼동 행렬을 시각화해 본다.
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
# Confusion Matrix 생성
cm = confusion_matrix(y_test, y_pred, labels=pipeline.classes_)
# Confusion Matrix 시각화
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=pipeline.classes_)
disp.plot(cmap=plt.cm.Blues)
plt.title("Confusion Matrix")
plt.show()
★ 크로스 엔트로피
크로스 엔트로피는 인공지능, 특히 딥러닝의 분류 문제에서 자주 사용되는 손실 함수(Loss Function) 중 하나이다. 크로스 엔트로피는 모델이 예측한 확률 분포와 실제 정답(레이블)의 확률 분포 간의 차이를 측정한다. 이를 통해 모델이 얼마나 "잘못된" 예측을 했는지 평가하고, 이 값을 최소화하면서 학습을 진행한다.
크로스 엔트로피의 특징
- 확률 기반: 모델이 출력하는 값은 항상 0~1 사이의 확률이어야 한다. 이를 위해 소프트맥스(Softmax) 함수와 함께 사용된다.
- 잘못된 예측에 큰 페널티: 예를 들어, 정답 클래스의 확률이 0.01처럼 매우 낮게 나올 경우 손실 값이 매우 커져 모델이 더 빠르게 학습하도록 유도한다.
★ 소프트맥스 함수(Softmax Function)
크로스 엔트로피와 함께 사용되며, 모델의 출력값을 확률로 변환하는 함수.
다음 내용
[딥러닝] 신경망 하이퍼파라미터 튜닝하기
인공 신경망 [딥러닝] 인공 신경망(ANN)머신러닝 기반 분석 모형 선정 [머신러닝] 머신러닝 기반 분석 모형 선정머신러닝 기반 분석 모형 선정 지도 학습, 비지도 학습, 강화 학습, 준지도 학
puppy-foot-it.tistory.com
[출처]
핸즈 온 머신러닝
https://jfun.tistory.com/48
'[파이썬 Projects] > <파이썬 딥러닝, 신경망>' 카테고리의 다른 글
| [딥러닝] 케라스로 다층 퍼셉트론 구현하기 - 2 (0) | 2024.11.20 |
|---|---|
| [딥러닝] 케라스로 다층 퍼셉트론 구현하기 - 1 (0) | 2024.11.19 |
| [딥러닝] 인공 신경망(ANN) (2) | 2024.11.19 |
| [딥러닝] Deep Learning 기본 개념 및 문제 (1) | 2024.09.25 |
| [Teachable Machine] 코딩없이 머신러닝 모델 만들기 - 2 (1) | 2024.09.24 |



