이전 내용
[딥러닝] 객체 탐지, 객체 추적
이전 내용 [딥러닝] 케라스의 사전 훈련 모델 사용하기이전 내용 [딥러닝] 합성곱 신경망을 사용한 컴퓨터 비전이전 내용 [딥러닝] 텐서플로 데이터셋 프로젝트텐서플로 [머신러닝] 텐서플로(Te
puppy-foot-it.tistory.com
순환 신경망(recurrent neural network, RNN)
RNN은 웹 사이트의 일일 활성 사용자 수, 도시의 시간별 기온, 가정의 일일 전력 소비량, 주변 차량의 궤적 등과 같은 시계열 데이터를 분석할 수 있다. 데이터에서 과거 패턴을 학습한 RNN은 과거 패턴이 미래에도 여전히 유효하다고 가정하고 그 지식을 사욯아여 미래를 예측할 수 있다.
일반적으로 RNN은 고정 길이 입력이 아닌 임의 길이의 시퀀스를 다룰 수 있는데, 예를 들어 문장, 문서, 오디오 샘플을 입력으로 받을 수 있다. 따라서 자동 번역, 스피치 투 텍스트 같은 자연어 처리에 매우 유용하다.
RNN이 순차 데이터를 다룰 수 있는 유일한 신경망은 아니다. 작은 시퀀스의 경우 일반적인 밀집 네트워크가 처리할 수 있고 오디오 샘플이나 텍스트처럼 매우 긴 시퀀스라면 합성곱 신경망도 실제로 잘 작동할 수 있다.
◆ RNN의 특징
- 순환 구조
RNN은 이전의 출력(Output)을 현재 입력(Input)과 결합하여 다음 단계로 전달하며, 이를 통해 과거 정보를 기억하고 이를 바탕으로 현재 상태를 예측하거나 처리할 수 있다.
- 시간 축 데이터에 강점
순차적인 데이터를 다룰 때 유리하며, 입력 데이터의 길이가 고정되지 않아도 처리할 수 있다.
- 메모리 특성
RNN은 데이터를 처리하면서, 이전 상태를 기억하는 "은닉 상태(hidden state)"를 유지한다.
◆ RNN 작동 원리
RNN은 데이터를 한 단계씩 처리하며, 이전 단계의 출력 값을 다음 단계의 입력 값으로 사용하는 구조를 가지고 있다.
- 입력 데이터
입력 데이터(예: 텍스트)를 일정한 순서로 제공.
예를 들어, 문장 "I love you"를 단어 단위로 처리한다고 가정.
- 은닉 상태 (Hidden State)
이전 단계에서 계산된 은닉 상태는 현재 단계의 입력 데이터와 함께 사용.
이 은닉 상태는 과거 정보를 기억하며, 새로운 데이터를 처리하는 데 활용.
- 출력 (Output)
마지막으로, 입력과 은닉 상태를 통해 출력 값을 생성.
예를 들어, 텍스트 분류에서는 문장이 긍정적인지 부정적인지 예측할 수 있다.
◆ RNN의 한계
- 장기 의존성 문제
RNN은 과거 정보가 길어질수록, 초반 입력 데이터를 잊어버리는 경향이 있다. 이를 "기울기 소실(Vanishing Gradient)" 문제라고 부른다.
- 느린 학습 속도
입력 데이터를 순차적으로 처리하기 때문에, 병렬 처리가 어려워 학습 속도가 느릴 수 있다.
◆ 개선된 RNN 모델
- LSTM (Long Short-Term Memory)
장기 의존성 문제를 해결하기 위해 고안된 모델로, 정보가 더 오래 기억되도록 설계되었다.
- GRU (Gated Recurrent Unit)
LSTM의 단순화된 버전으로, 계산량을 줄이면서도 성능을 유지한다.
입력과 출력 시퀀스
1) 시퀀스-투-시퀀스 네트워크
RNN은 입력 시퀀스를 받아 출력 시퀀스를 만들 수 있는데, 이를 시퀀스-투-시퀀스 네트워크라고 하며, 가정의 일일 전력 사용량 같은 시계열 데이터를 예측하는 데 유용하다. 최근 N일치의 전력 사용량을 주입하면 네트워크는 각 입력값보다 하루 앞선 미래의 전력 사용량을 출력해야 한다.
2) 시퀀스-투-벡터 네트워크
입력 시퀀스를 네트워크에 주입하고 마지막을 제외한 모든 출력을 무시할 수 있는데, 이를 시퀀스-투-벡터 네트워크라고 하며, 영화 리뷰에 있는 연속된 단어를 주입하면 네트워크는 감성 점수를 출력하는 데 유용하다.
3) 벡터-투-시퀀스 네트워크
각 타임 스텝에서 하나의 입력 벡터를 반복해서 네트워크에 주입하고 하나의 시퀀스를 출력할 수 있는데, 이를 벡터-투-시퀀스 네트워크라고 하며, 이미지를 입락하여 이미지에 대한 캡션을 출력할 수 있다.
4) 인코더-디코더
인코더라 부르는 시퀀스-투-벡터 네트워크에 디코더라 부르는 벡터-투-시퀀스 네트워크를 연결할 수 있다. 예를 들어 한 언어의 문장을 다른 언어로 번역하는 데 사용할 수 있는데, 한 언어의 문장을 네트워크에 주입하면 인코더는 이 문장을 하나의 벡터 표현으로 표현하고, 디코더가 이 벡터를 다른 언어의 문장으로 디코딩한다. 이런 이중 단계 모델은 하나의 시퀀스-투-시퀀스 RNN을 사용하여 한 단어씩 번역하는 것보다 훨씬 더 잘 작동하는 데, 문장의 마지막 단어가 번역의 첫 번째 단어에 영향을 줄 수 있기 때문이다. 그래서 번역하기 전에 전체 문장이 주입될 때까지 기다릴 필요가 있다.
시계열 예측하기
시카고 교통국 일일 승객 데이터를 가지고 다음날 버스와 열차에 탑승할 승객 수를 예측하는 모델을 만드는 프로젝트를 해본다.

※ csv 파일은 캐글에서 다운로드 받았다.
Chicago Transit Authority (CTA) Data
Explore Open Data from the City of Chicago
www.kaggle.com

먼저 데이터를 로드하고 정제한다.
import pandas as pd
from pathlib import Path
df = pd.read_csv("C:/Users/niceq/Documents/DataScience/Hands_ML/Data/15. cta-ridership-daily-boarding-totals.csv", parse_dates=['service_date'])
df.columns = ['date', 'day_type', 'bus', 'rail', 'total'] # 짧은 이름
df = df.sort_values('date').set_index('date')
df = df.drop('total', axis=1) # total = bus + rail
df = df.drop_duplicates() # 중복 월 삭제
# 모든 열을 숫자형으로 변환
df[['bus', 'rail']] = df[['bus', 'rail']].apply(pd.to_numeric, errors='coerce')
# NaN 값 처리
df = df.fillna(method='ffill').fillna(method='bfill')
df.head()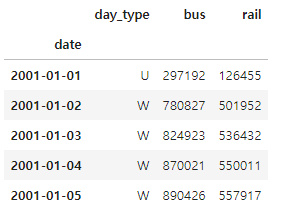
▶ csv 파일을 로드하고, 열 이름을 줄이고, 날짜순으로 행을 정렬하고, total 열을 삭제하고, 중복 행을 삭제한 뒤.
모든 열을 숫자형으로 변환하고, NaN 값 처리 후 상단 5개의 행을 출력했다.
day_type의 경우 평일(W), 토요일(A), 일요일 또는 공휴일(U)
2019년 몇 달 동안의 버스와 열차 승객 수를 그래프로 그려본다.
df['2019-03':'2019-05'].plot(grid=True, marker='.', figsize=(8, 3.5))
plt.show()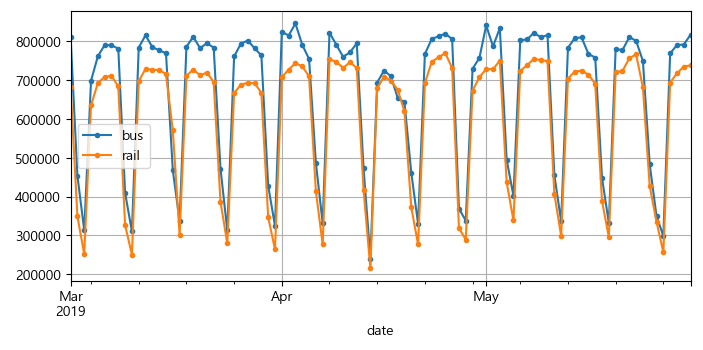
▶ 판다스는 지정한 범위의 시작과 끝을 모두 포함시키므로, 이 그래프는 3월 1일부터 5월 31일까지의 데이터를 그리는 시계열 그래프이다. 또한, 일반적으로 일정한 간격의 타임 스텝별 값을 가진 데이터이며, 타입 스텝마다 여러 개의 값이 있기 때문에 다변량 시계열이다.
bus나 rail 각각의 열만 본다면 타임 스텝마다 하나의 값이 있기 때문에 단변량 시계열이다.
시계열을 다룰 때 가장 일반적인 작업은 미래의 값을 예측하는 것이다.
상단의 그래프를 보면 매주 비슷한 패턴이 반복되는 주간 계절성을 띄는데, 이 경우 패턴이 매우 강력해서 일주일 전 값을 내일 승객 수로 예측해도 매우 좋은 결과를 얻을 수 있다. 이를 단순 예측이라고 하는데, 과거 값을 단순히 복사해 예측을 만드는 것이다. 단순 예측은 훌륭한 기준점이 된다.
일반적으로 단순 예측은 가장 최근 값 즉, 오늘 값을 복사해 내일 값을 예측하는 것을 의미하는데, 이 경우엔 강한 주간 계절성 때문에 일주일 전 값을 사용하는 것이 더 좋다.
단순 예측 결과를 시각화하기 위해 버스와 열차에 대한 시계열과 함께 일주일 지연된 시계열을 점선으로 그려보고, 두 시계열의 차이(차분)을 그려본다.
diff_7 = df[['bus', 'rail']].diff(7)['2019-03':'2019-05']
fig, axs = plt.subplots(2, 1, sharex=True, figsize=(8, 5))
df.plot(ax=axs[0], legend=False, marker='.') # 원본 시계열
df.shift(7).plot(ax=axs[0], grid=True, legend=False, linestyle=':') # 지연된 시계열
diff_7.plot(ax=axs[1], grid=True, marker='.') # 7일간의 차이
plt.show()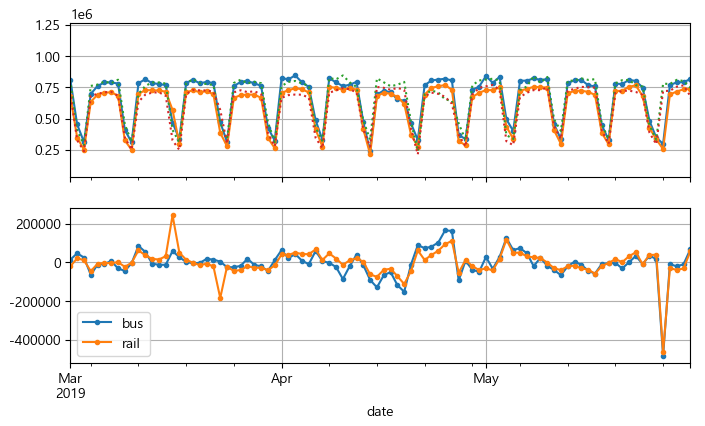
▶ 지연된 시계열이 실제 시계열을 잘 따라고 있다. 시계열이 시간이 지연된 자기자신과 상관관계를 가질 때 이를 자기상관 시계열이라고 한다.
5월 말을 제외하고는 대부분 차이가 적은데, 이때 공휴일이 있었는지 확인해본다.
list(df.loc['2019-05-25':'2019-05-27']['day_type'])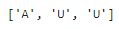
▶ 25일은 토요일(A), 26일은 일요일(U), 27일(월)은 공휴일(U)이다.
임의로 선택한 2019년 3~5월 3달 동안의 평균 절댓값 오차(MAE)를 계산해본다.
diff_7.abs().mean()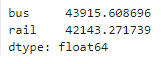
▶ 단순 예측의 MAE는 버스의 경우 약 43,916명, 기차의 경우 약 42,144명이다.
예측 오차를 타깃값으로 나누어본다.
targets = df[['bus','rail']]['2019-03':'2019-05']
(diff_7 / targets).abs().mean()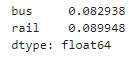
▶ 이 값을 평균 절대 비율 오차(MAPE)라고 부르는데, 버스의 경우 대략 8.3%, 기차의 경우 대략 9.0%이다.
이 데이터셋의 연간 계절성도 확인해보기 위해 2001년부터 2019년까지 데이터를 살펴본다. 장기간 트렌드를 시각화하기 위해 각 시계열의 12개월 이동 평균을 그려본다. (데이터 스누핑의 위험을 줄이기 위해 최신 데이터를 잠시 무시한다.)
# 기간 설정
period = slice('2001', '2019')
# 데이터프레임을 월간 평균으로 리샘플링
df_monthly = df.resample('M').mean()
# 12개월 이동 평균 계산
rolling_average_12_months = df_monthly[period].rolling(window=12).mean()
# 시각화
fig, ax = plt.subplots(figsize=(8, 4))
df_monthly[period].plot(ax=ax, marker='.')
rolling_average_12_months.plot(ax=ax, grid=True, legend=False)
plt.show()※ 이 코드를 입력하면 'TypeError: agg function failed [how->mean,dtype->object]' 가 뜨는데, 이 에러는
숫자가 아닌 데이터가 포함된 열에 대해 평균과 같은 집계 작업을 수행하려고 할 때 발생한다.
- agg function failed: 집계 함수가 문제를 발견
- [how->mean, : 평균 함수를 집계 방법으로 사용하려고 하고 있음을 나타냄.
- dtype->object]: 집계하려는 열의 데이터 유형이 'object' 임을 나타냄. (숫자가 아닌 데이터)
따라서, 이 문제를 해결하려면 집계하려는 열이 숫자 데이터를 포함하는지 확인해야 한다.
df.info()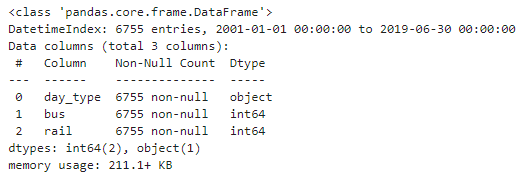
day_type의 데이터 타입이 object라서 해당 코드가 오류가 발생했던 것인데, 이를 위한 해결 방법은
1) day_type 칼럼을 삭제하고 bus 칼럼과 train 칼럼의 평균을 계산한다.
2) day_type 칼럼을 삭제하지 않고 계산에서만 제외하여 bus 칼럼과 train 칼럼의 평균을 계산한다.
day_type 칼럼이 해당 데이터에서 중요할 수 있으므로, 2번 방법을 사용하기로 한다.
# 기간 설정
period = slice('2001', '2019')
# 숫자형 변수들만 따로 추출
df_numeric = df[['bus', 'rail']]
# 데이터프레임을 월간 평균으로 리샘플링
df_monthly = df_numeric.resample('M').mean()
# 12개월 이동 평균 계산
rolling_average_12_months = df_monthly[period].rolling(window=12).mean()
# 시각화
fig, ax = plt.subplots(figsize=(8, 4))
df_monthly[period].plot(ax=ax, marker='.')
rolling_average_12_months.plot(ax=ax, grid=True, legend=False)
plt.show()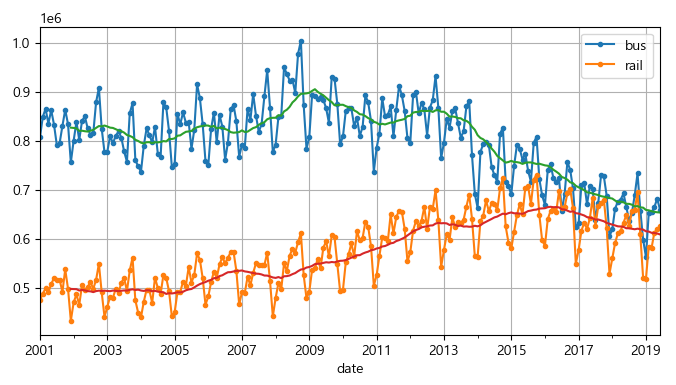
▶ 문제없이 그래프가 잘 그려졌다.
해당 그래프를 통해 본 연간 계절성은 버스 시계열보다 열차 시계열에서 더 잘 보이며, 매년 거의 같은 날짜에서 최고점과 최저점을 볼 수 있다. 12개월 차분을 그려서 다시 확인해본다.
df_monthly.diff(12)[period].plot(grid=True, marker='.', figsize=(8, 3))
plt.show()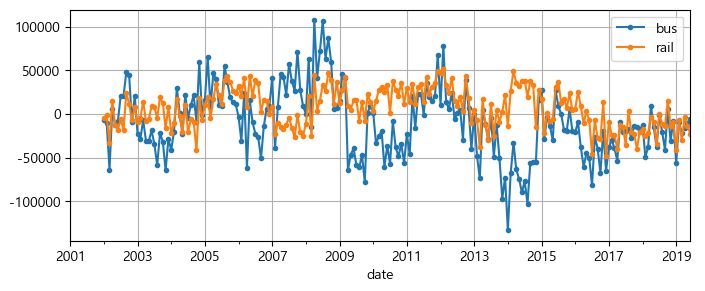
차분은 시계열에서 트렌드와 계절성을 제거하기 위해 사용되는 대표적인 기법으로, 계절성이나 트렌드가 없어 시간에 따라 통계적 속성이 일정한 정상 시계열을 분석하는 것이 더 쉽다.
차분 시계열에서 정확한 예츠글 수행할 수 있다면 이전에 차감한 과거 값을 다시 더해서 실제 시계열에 대한 예측으로 쉽게 바꿀 수 있다.
ARMA, ARIMA, SARIMA 모델
ARMA, ARIMA, 그리고 SARIMA 모델들은 시간에 따라 변동하는 데이터를 분석하고 예측하는데 사용되는 통계적 모델이다. 이들 모델은 각각 다른 데이터 특성에 따라 적합한 모델을 선택할 수 있도록 다양한 구성 요소들을 포함한다.
- ARMA: 정상 시계열 데이터를 다루는 자기회귀 이동평균 모델
- ARIMA: 비정상 시계열 데이터를 다루기 위해 차분을 포함한 모델
- SARIMA: 계절성을 갖는 시계열 데이터를 다루는 데 사용하는 모델
1. ARMA (AutoRegressive Moving Average) - 자기 회귀 이동 평균
ARMA 모델은 자기회귀(AR) 모델과 이동평균(MA) 모델을 결합한 것으로, 이는 시계열 데이터가 정상적(stationary)인 경우에 주로 사용된다. ARMA 모델은 두 가지 구성요소로 이루어져 있다.
- AR (AutoRegressive) 부분: 과거의 값을 이용하여 현재의 값을 예측한다. 예를 들어, AR(1) 모델은 바로 직전 시점의 데이터를 이용하여 현재 시점을 예측한다.
- MA (Moving Average) 부분: 과거의 예측 오차를 이용하여 현재의 값을 예측한다. 예를 들어, MA(1) 모델은 직전 시점의 예측 오차를 활용한다.
2. ARIMA (AutoRegressive Integrated Moving Average) - 자기 회귀 누적 이동 평균
ARIMA 모델은 ARMA 모델을 확장한 것으로, 비정상(non-stationary) 데이터를 다루기 위해 차분(diffrecing) 과정을 추가한다. 차분은 데이터를 정상 상태로 만든다.
- I (Integrated) 부분: 데이터의 차분을 의미한다. 예를 들어, 1차 차분을 통해 데이터의 추세를 제거하여 정상성을 확보한다.
[Y_t’ = Y_t - Y_{t-1}]
ARIMA(p,d,q) 모델은 다음과 같이 설정된다:
- (p): 자기회귀 부분의 시차(lag) 수
- (d): 차분의 차수 (일반적으로 1 또는 더 높은 차수)
- (q): 이동평균 부분의 시차 수
3. SARIMA (Seasonal ARIMA) - 계절성 ARIMA 모델
SARIMA 모델은 계절성을 가지는 시계열 데이터를 분석 및 예측하는 데 사용된다. 이는 ARIMA 모델에 계절적 요인을 포함한 모델이다. SARIMA 모델은 다음과 같은 7개의 매개변수를 가진다:
- (p,d,q): ARIMA 모델의 매개변수 (자기회귀 부분, 차분, 이동평균)
- (P,D,Q, s): 계절적 부분의 매개변수
- (P): 계절적 자기회귀 부분의 시차 수
- (D): 계절적 차분의 차수
- (Q): 계절적 이동평균 부분의 시차 수
- (s): 계절 주기 (예: 12개월 주기)
오늘을 2019년 5월 31일이라 가정하고 열차 시계열에 SARIMA 모델을 적용해서 내일(2019년 6월 1일)의 승객 수를 예측해본다. 이를 위해 ARIMA 모델과 여러 변형을 포함해 여러 가지 통계 모델을 제공하는 statsmodels 라이브러리를 사용할 수 있다.
from statsmodels.tsa.arima.model import ARIMA
origin, today = '2019-01-01', '2019-05-31'
rail_series = df.loc[origin:today]['rail'].asfreq('D')
model = ARIMA(rail_series,
order=(1, 0, 0),
seasonal_order=(0, 1, 1, 7))
model = model.fit()
y_pred = model.forecast()
y_pred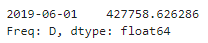
[코드 설명]
- ARIMA 클래스를 먼저 임포트한 다음, asfreq('D')를 사용하여 2019년 5월 말까지 열차 승객 데이터 빈도를 일자별로 설정. 이렇게 하지 않으면 ARIMA 클래스가 빈도를 예측해야 하므로 경고 출력
- 5월 말까지 전체 데이터를 전달하여 ARIMA 클래스이 인스턴스를 만든다. 모델 하이퍼파라미터 order=(1, 0, 0)은 p=1, d=0, q=0을 의미하며, seasonal_order=(0, 1, 1, 7)은 P=0, D=1, Q=1, s=7을 의미한다.
- statsmodels API는 사이킷런과 조금 다르기 때문에, fit() 메서드가 아니라 모델 생성 시점에 데이터를 전달한다.
- 모델을 훈련하고 다음 날인 2019년 6월 1일에 대한 예측을 만든다.
df.loc['2019-06-01']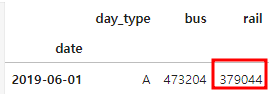
▶ 예측 승객 수는 427,759명이고, 실제 승객 수는 379,044명으로 12.9%나 차이가 나므로 좋은 예측이라고 볼 수 없다.
동일한 코드를 반복문으로 감싸서 3월, 4월, 5월의 모든 날에 대한 예측을 만들고 전체 기간에 대한 MAE를 계산해본다.
origin, start_date, end_date = '2019-01-01', '2019-03-01', '2019-05-31'
time_period = pd.date_range(start_date, end_date)
rail_series = df.loc[origin:end_date]['rail'].asfreq('D')
y_preds = []
for today in time_period.shift(-1):
model = ARIMA(rail_series[origin:today], # today까지 데이터로 훈련
order=(1, 0, 0),
seasonal_order=(0, 1, 1, 7))
model = model.fit() # 매일 모델 재훈련
y_pred = model.forecast()[0]
y_preds.append(y_pred)
y_preds = pd.Series(y_preds, index=time_period)
mae = (y_preds - rail_series[time_period]).abs().mean()
mae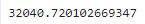
▶ MAE가 약 32,041로 단순 예측의 MAE(42,143) 보다 크게 낮으므로, 단순 예측의 성능보다 좋다.
SARIMA 모델의 하이퍼파라미터를 선택하는 방법 중 가장 이해하기 쉽고 시작하기 쉬운 방법은 단순한 GridSearch 이다. 평가하려는 각 하이퍼파라미터의 조합에 대해 하이퍼파라미터 값만 바꾸면서 코드를 실행하면 되는데, p, q, P, Q 값은 일반적으로 매우 작고(보통 0~2, 간혹 6정도까지) , 좋은 d, D는 일반적으로 0 또는 1이다.
s는 계절성 패턴의 기간이며, 이 예제의 경우 강한 주간 계절성을 가지므로 7이며, 가장 낮은 MAE를 내는 모델이 최상의 모델이다. (비즈니스 목표에 맞게 MAE를 다른 지표로 바꿀 수 있다.)
다음 내용
[딥러닝] RNN & CNN(feat. 시카고 교통국 데이터셋) - 2
이전 내용 [딥러닝] RNN & CNN(feat. 시카고 교통국 데이터셋) - 1이전 내용 [딥러닝] 객체 탐지, 객체 추적이전 내용 [딥러닝] 케라스의 사전 훈련 모델 사용하기이전 내용 [딥러닝] 합성곱 신경망
puppy-foot-it.tistory.com
[출처]
핸즈 온 머신러닝
https://data.cityofchicago.org/
https://taehi-dev.tistory.com/466
'[파이썬 Projects] > <파이썬 딥러닝, 신경망>' 카테고리의 다른 글
| [딥러닝] RNN & CNN(feat. 시카고 교통국 데이터셋) - 3 (1) | 2024.12.02 |
|---|---|
| [딥러닝] RNN & CNN(feat. 시카고 교통국 데이터셋) - 2 (1) | 2024.12.01 |
| [딥러닝] 객체 탐지, 객체 추적 (0) | 2024.11.29 |
| [딥러닝] 케라스의 사전 훈련 모델 사용하기 (1) | 2024.11.29 |
| [딥러닝] 합성곱 신경망을 사용한 컴퓨터 비전 (0) | 2024.11.27 |



