앙상블 학습(Ensemble Learning)
[파이썬] 분류: 앙상블 학습(Ensemble Learning) - 1
시작에 앞서해당 내용은 ' 권철민 지음. 위키북스' 를 토대로 작성되었습니다. 보다 자세한 내용은 해당 서적에 상세히 나와있으니 서적을 참고해 주시기 바랍니다.앙상블 학습(Ensemble Learning)
puppy-foot-it.tistory.com
부스팅 알고리즘
부스팅 알고리즘: 여러 개의 약한 학습기를 순차적으로 학습-예측 하면서 잘못 예측한 데이터에 가중치 부여를 통해 오류를 개선해 나가면서 학습하는 방식.
[부스팅의 대표적인 구현]
- AdaBoost: 오류 데이터에 가중치를 부여하면서 부스팅을 수행하는 대표적인 알고리즘
- GBM: AdaBoost와 유사하나, 가중치 업데이트를 경사 하강법(Gradient Descent)을 이용
GBM은 AdaBoost처럼 앙상블에 이전까지의 오차를 보정하도록 예측기를 순차적으로 추가한다. 하지만 AdaBoost처럼 반복마다 샘플의 가중치를 수정하는 대신 이전 예측기가 만든 잔여 오차(residual error)에 새로운 예측기를 학습시킨다.
GBM
◆ 가중치 업데이트를 경사 하강법(Gradient Descent)을 이용
※ 경사하강법: 반복 수행을 통해 오류를 최소화할 수 있도록 가중치의 업데이트 값을 도출하는 기법
GBM은 CART 기반의 다른 알고리즘과 마찬가지로 분류와 회귀가 가능하며, 사이킷런은 GBM 기반의 분류를 위해서 GradientBoostingClassifier 클래스를 제공한다.
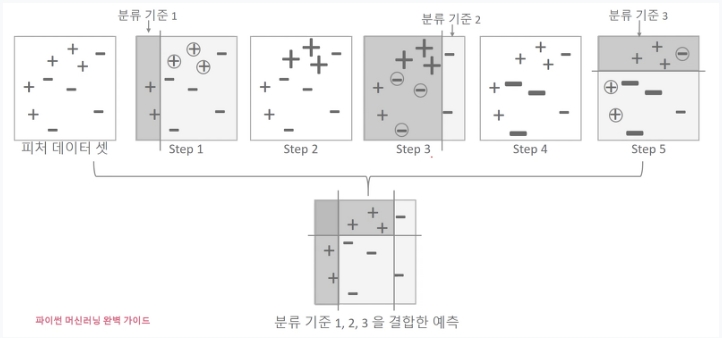
- step 1은 첫 번째 weak learner가 분류 기준 1+와 -를 분류한 것이며, 동그라미로 표시된 + 데이터는 +데이터가 잘못 분류된 오류 데이터
- step 2에서는 이 오류 데이터에 대해 가중치 부여. 가중치가 부여된 오류 + 데이터는 다음 weak learner가 더 잘 분류할 수 있게 크기가 커짐
- step 3은 두 번째 weak learner가 분류 기준 2로 +와 -를 분류. 동그라미로 표시된 - 데이터는 분류된 오류 데이터
- step 4에서는 잘못 분류된 이 - 오류 데이터에 대해 다음 weak learner 가 잘 분류할 수 있게 더 큰 가중치를 부여(오류 - 데이터 크기 커짐)
- setp 5는 세 번째 weak learner가 분류 기준 3으로 +와 -를 분류하고 오류 데이터를 찾음.
- 마지막으로 맨 아래에는 첫 번째, 두 번째, 세 번째 약한 학습기(weak learner)를 모두 결합한 결과 예측. (개별 약한 학습기보다 정확도가 훨씬 높아짐)
결정 트리를 기반 예측기로 사용한 회귀 (GBM)
결정 트리를 기반 예측기로 사용하는 간단한 회귀 문제를 풀어보는데, 먼저 2차 방정식으로 잡음이 섞인 데이터셋을 생성하고 DecisionTreeRegressor를 학습시켜본다.
import numpy as np
from sklearn.tree import DecisionTreeRegressor
np.random.seed(42)
X = np.random.rand(100, 1) - 0.5
y = 3 * X[:, 0] ** 2 + 0.05 * np.random.randn(100) # y = 3x^2 가우스_잡음
tree_reg1 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg1.fit(X, y)
이제 첫 번째 예측기에서 생긴 잔여 오차(residual error)에 두 번째 DecisionTreeRegressor를 훈련시킨다
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth=2, random_state=43)
tree_reg2.fit(X, y2)
그런 다음 두 번째 예측기가 만든 잔여 오차에 세 번째 회귀 모델을 훈련시킨다.
y3 = y2 - tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth=2, random_state=44)
tree_reg3.fit(X, y3)
이제 세 개의 트리를 포함하는 앙상블 모델이 생겼다.
만약 새로운 샘플에 대한 예측을 만들려면 모든 트리의 예측을 더하면 된다.
X_new = np.array([[-0.4,], [0.], [0.5]])
sum(tree.predict(X_new) for tree in (tree_reg1, tree_reg2, tree_reg3))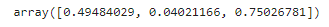
아래 코드를 통해 나타난 그래프의 왼쪽 열은 이 세 트리의 예측이고, 오른쪽 열은 앙상블의 예측이다.
def plot_predictions(regressors, X, y, axes, style,
label=None, data_style="b.", data_label=None):
x1 = np.linspace(axes[0], axes[1], 500)
y_pred = sum(regressor.predict(x1.reshape(-1, 1))
for regressor in regressors)
plt.plot(X[:, 0], y, data_style, label=data_label)
plt.plot(x1, y_pred, style, linewidth=2, label=label)
if label or data_label:
plt.legend(loc="upper center")
plt.axis(axes)
plt.figure(figsize=(11, 11))
plt.subplot(3, 2, 1)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.2, 0.8], style="g-",
label="$h_1(x_1)$", data_label="훈련 세트")
plt.ylabel("$y$ ", rotation=0)
plt.title("잔여 오차와 트리의 예측")
plt.subplot(3, 2, 2)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.2, 0.8], style="r-",
label="$h(x_1) = h_1(x_1)$", data_label="훈련 세트")
plt.title("앙상블의 예측")
plt.subplot(3, 2, 3)
plot_predictions([tree_reg2], X, y2, axes=[-0.5, 0.5, -0.4, 0.6], style="g-",
label="$h_2(x_1)$", data_style="k+",
data_label="잔여 오차: $y - h_1(x_1)$")
plt.ylabel("$y$ ", rotation=0)
plt.subplot(3, 2, 4)
plot_predictions([tree_reg1, tree_reg2], X, y, axes=[-0.5, 0.5, -0.2, 0.8],
style="r-", label="$h(x_1) = h_1(x_1) + h_2(x_1)$")
plt.subplot(3, 2, 5)
plot_predictions([tree_reg3], X, y3, axes=[-0.5, 0.5, -0.4, 0.6], style="g-",
label="$h_3(x_1)$", data_style="k+",
data_label="잔여 오차: $y - h_1(x_1) - h_2(x_1)$")
plt.xlabel("$x_1$")
plt.ylabel("$y$ ", rotation=0)
plt.subplot(3, 2, 6)
plot_predictions([tree_reg1, tree_reg2, tree_reg3], X, y,
axes=[-0.5, 0.5, -0.2, 0.8], style="r-",
label="$h(x_1) = h_1(x_1) + h_2(x_1) + h_3(x_1)$")
plt.xlabel("$x_1$")
plt.show()
- 첫 번째 행: 앙상블에 트리가 하나만 있어서 첫 번째 트리의 예측과 완전히 같다
- 두 번째 행: 새로운 트리가 첫 번재 트리의 잔여 오차에 학습되어 오른쪽의 앙상블 예측이 두 개의 트리 예측의 합과 같다
- 새 번째 행: 또 다른 트리가 두 번째 트리의 잔여 오차에 훈련되었다.
▶ 트리가 앙상블에 추가될수록 앙상블의 예측이 점차 좋아지는 것을 알 수 있다.
사이킷런에서의 GBRT 앙상블 훈련
사이킷런에서는 사이킷런의 GradientBoostingRegressor를 사용하면 GBRT (Gradient Boosted Regression Tree, 그레이디언트 부스티드 회귀 트리) 앙상블을 간단하게 훈련시킬 수 있다. (분류를 위한 클래스는 GradientBoostingClassifier)
트리 수(n_estimators)와 같이 앙상블의 훈련을 제어하는 매개변수는 물론 RandomForestRegressor와 아주 비슷하게 결정 트리의 성장을 제어하는 매개변수(max_depth, min_sample_leaf)를 가지고 있다.
from sklearn.ensemble import GradientBoostingRegressor
gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=3,
learning_rate=1.0, random_state=42)
gbrt.fit(X, y)
learning_rate 매개변수가 각 트리의 기여도를 조절하는데, 0.05처럼 낮게 설정하면 앙상블을 훈련 세트에 학습시키기 위해 많은 트리가 필요하지만 일반적으로 예측의 성능은 좋아진다. (이는 축소라고 불리는 규제 방법이다)
◆ 조기 종료를 사용한 앙상블 훈련
최적의 트리 개수를 찾으려면 GridSearchCV 또는 RandomizedSearchCV를 사용하여 교차 검증을 수행할 수 있지만 더 간단한 방법이 있다. n_iter_no_change 하이퍼파라미터를 정숫값(예. 10)으로 설정하면 훈련 중에 마지막 10개의 트리가 도움이 되지 않는 경우 GradientBoostingRegressor가 트리 추가를 자동으로 중지한다.
이것은 단순한 조기 종료 기법이지만 약간의 인내심을 가지고 몇 번의 반복에서 진전이 없는 것을 확인한 후 중지한다.
gbrt_best = GradientBoostingRegressor(
max_depth=2, learning_rate=0.05, n_estimators=500,
n_iter_no_change=10, random_state=42)
gbrt_best.fit(X, y)gbrt_best.n_estimators_
n_iter_no_change를 설정하면 fit() 메서드가 자동으로 훈련 세트를 더 작은 훈련 세트와 검증 세트로 분할하므로 새 트리를 추가할 때마다 모델의 성능을 평가할 수 있다.
검증 세트의 크기는 validation_fraction 하이퍼파라미터에 의해 제어되며, 기본값은 10%이다.
tol 하이퍼파라미터는 무시할 수 있는 최대 성능 향상을 결정하며 기본값은 0.0001 이다.
◆ 확률적 그레이디언트 부스팅(stochastic gradient boosting)
GradientBoostingRegressor는 각 트리가 훈련될 때 사용할 훈련 샘플의 비율을 지정할 수 있는 subsample 매개변수도 지원한다. 예를 들어 subsample=0.25라고 하면 각 트리는 랜덤으로 선택된 25%의 훈련 샘플로 학습된다. 이런 경우 편향이 높아지는 대신 분산이 낮아지며, 훈련 속도도 상당히 빨라진다.
아래는 다른 하이퍼파라미터로 훈련시킨 두 개의 GBRT 앙상블을 보여준다.
fig, axes = plt.subplots(ncols=2, figsize=(10, 4), sharey=True)
plt.sca(axes[0])
plot_predictions([gbrt], X, y, axes=[-0.5, 0.5, -0.1, 0.8], style="r-",
label="앙상블의 예측")
plt.title(f"learning_rate={gbrt.learning_rate}, "
f"n_estimators={gbrt.n_estimators_}")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.sca(axes[1])
plot_predictions([gbrt_best], X, y, axes=[-0.5, 0.5, -0.1, 0.8], style="r-")
plt.title(f"learning_rate={gbrt_best.learning_rate}, "
f"n_estimators={gbrt_best.n_estimators_}")
plt.xlabel("$x_1$")
plt.show()
▶왼쪽은 훈련 세트를 학습하기에는 트리가 충분하지 않은 반면, 오른쪽은 적정한 개수의 트리를 사용한다.
만약 트리를 더 추가하면 GBRT가 훈련 세트에 과대적합되기 시작할 것이다.
히스토그램 기반 그레이디언트 부스팅(HGB)
사이킷런은 대규모 데이터셋에 최적화된 또 다른 GBRT 구현인 히스토그램 기반 그레이디언트 부스팅(Histogram-based gradient boosting, HGB)도 제공한다. 이 알고리즘은 입력 특성을 구간으로 나누어 정수로 대체하는 방식으로 작동하며, 구간의 개수는 max_bins 하이퍼파라미터에 의해 제어되며, 기본값은 255이고 이보다 높게 설정할 수 없다.
구간 분할을 사용하면 학습 알고리즘의 평가해야 하는 가능한 임곗값의 수를 크게 줄일 수 있고, 정수로 작업하면 더 빠르고 메모리 효율적인 데이터 구조를 사용할 수 있다.
또한 구간을 분할하는 방식 덕분에 각 트리를 학습할 때 특성을 정렬할 필요가 없다.
이 구현의 계산 복잡도는 O(b*m) 이며,
- b: 구간의 개수
- m: 훈련 샘플의 개수
이는 실제로 HGB가 대규모 데이터셋에서 일반 GBRT 보다 수백 배 빠르게 훈련할 수 있다는 것을 의미한다. 그러나 구간 분할은 규제처럼 작동해 정밀도 손상을 유발하므로 데이터셋에 따라 과대적합을 줄이는 데 도움이 될 수도 있고 과소적합을 유발할 수도 있다.
[사이킷런에서의 HGB 구현]
- 회귀: HistGradientBoostingRegressor
- 분류: HistGradientBoostingClassifier
이 두 클래스는 GradientBoostingRegressor, GradientBoostingClassifier 와 유사하지만 몇 가지 차이점이 있다.
- 인스턴스 수가 10,000개보다 많으면 조기 종료가 자동으로 활성화 된다. ▶ early_stopping 매개변수를 True 또는 False로 설정하여 조기 종료를 항상 켜거나 끌 수 있다.
- subsample 매개변수가 지원되지 않는다
- n_estimators 매개변수가 max_iter 로 바뀌었다
- 조정할 수 있는 결정 트리 하이퍼파라미터는 max_leaf_nodes, min_samples_leaf, max_depth 뿐이다.
HGB 클래스는 범주형 특성과 누락된 값을 지원하여 전처리가 상당히 간소화된다. 그러나 범주형 특성은 0 ~ max_bins 사이의 정수로 표현해야 하며, 이를 위해 OrdinalEncoder를 사용할 수 있다.
[캘리포니아 주택 데이터셋에 대한 전체 파이프라인을 구축하고 훈련하는 방법]
먼저, 캘리포니아 주택 데이터셋을 불러온다.
import pandas as pd
from sklearn.model_selection import train_test_split
from pathlib import Path
import tarfile
import urllib.request
# 캘리포니아 주택 데이터셋 불러오기
def load_housing_data():
tarball_path = Path("datasets/housing.tgz")
if not tarball_path.is_file():
Path("datasets").mkdir(parents=True, exist_ok=True)
url = "https://github.com/ageron/data/raw/main/housing.tgz"
urllib.request.urlretrieve(url, tarball_path)
with tarfile.open(tarball_path) as housing_tarball:
housing_tarball.extractall(path="datasets")
return pd.read_csv(Path("datasets/housing/housing.csv"))
housing = load_housing_data()
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
housing_labels = train_set["median_house_value"]
housing = train_set.drop("median_house_value", axis=1)
불러온 캘리포니아 주택 데이터셋에 대한 전체 파이프라인 구축 및 훈련 (HGB 사용)
from sklearn.pipeline import make_pipeline
from sklearn.compose import make_column_transformer
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.preprocessing import OrdinalEncoder
# HGB로 파이프라인 구축 및 훈련
hgb_reg = make_pipeline(
make_column_transformer((OrdinalEncoder(), ['ocean_proximity']),
remainder='passthrough'),
HistGradientBoostingRegressor(categorical_features=[0], random_state=42)
)
hgb_reg.fit(housing, housing_labels)
▶ 전처리(누락된 값 채우기, 스케일 조정, 원-핫 인코딩)를 하지 않아도 되어 매우 편리하다.
범주형 열의 인덱스 (또는 boolean 배열)로 categorical_features를 설정해야 한다는 점에 유의.
해당 모델에 대한 RMSE 계산
from sklearn.model_selection import cross_val_score
hgb_rmses = -cross_val_score(hgb_reg, housing, housing_labels,
scoring="neg_root_mean_squared_error", cv=10)
pd.Series(hgb_rmses).describe()
▶ 하이퍼파라미터 튜닝 없이도 약 47,600의 RMSE를 산출한다.
GBM을 이용한 사용자 행동 데이터 세트 예측 분류
# # GBM (사용자 행동 인식 데이터 세트 활용)
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import accuracy_score
import pandas as pd
import warnings
warnings.filterwarnings('ignore')# GBM
import time
X_train, X_test, y_train, y_test = get_human_dataset()
#GBM 수행 시간 측정을 위함. 시작 시간 설정
start_time = time.time()
gb_clf = GradientBoostingClassifier(random_state=0)
gb_clf.fit(X_train, y_train)
gb_pred = gb_clf.predict(X_test)
gb_accuracy = accuracy_score(y_test, gb_pred)
print('GBM 정확도: {0:.4f}'.format(gb_accuracy))
print("GBM 수행시간: {0:.4f} 초". format(time.time() - start_time))
▶ 기본 하이퍼 파라미터 만으로도 랜덤 포레스트(91.96%) 보다도 나은 예측 성능을 나타내지만, 수행 시간이 오래 걸린다.
사이킷런의 GradientBoostingClassifier 는 약한 학습기의 순차적인 예측 오류 보정을 통해 학습을 수행하므로 멀티 CPU 코어 시스템을 사용하더라도 병렬처리가 지원되지 않아서 대용량 데이터의 경우 학습에 매우 많은 시간이 필요하다.
(랜덤 포레스트는 예측 성능이 보다 낮으나, 상대적으로 빠른 수행 시간을 보장)
GBM 하이퍼 파라미터
n_estimators, max_depth, max_features 와 같은 트리 기반 자체의 파라미터는 하단 내용 참고
[파이썬] 분류 > 앙상블 - 2 : 랜덤 포레스트
시작에 앞서해당 내용은 ' 권철민 지음. 위키북스' 를 토대로 작성되었습니다. 보다 자세한 내용은 해당 서적에 상세히 나와있으니 서적을 참고해 주시기 바랍니다.앙상블 학습(Ensemble Learning) [
puppy-foot-it.tistory.com
- loss: 경사 하강법에서 사용할 비용 함수 지정. (디폴트는 deviance)
- learning_rate: GBM이 학습을 진행할 때마다 적용하는 학습률. Weak learner 가 순차적으로 오류 값을 보정해 나가는 데 적용하는 계수. (0~1 사이의 값. 기본값은 0.1)
▶ 너무 작은 값 입력 시: 업데이트 되는 값이 작아져 최소 오류 값을 찾아 예측 성능이 높아질 가능성이 높음. 많은 weak learner는 수행 시간이 오래 걸리고, 모든 weak learner의 반복이 완료돼도 최소 오류 값을 찾지 못할 수 있음.
▶ 너무 큰 값 적용 시: 최소 오류 값을 찾지 못하고 그냥 지나쳐 버려 예측 성능이 떨어질 가능성이 높으나, 수행시간이 짧음.
따라서, learning_rate는 n_estimators와 상호 보완적으로 조합해 사용. (수행 시간 오래 걸림)
- n_estimators: weak learners의 개수. 개수가 많을수록 예측 성능 좋아지나, 수행 시간 오래 걸림. 기본값은 100
- subsample: weak learner가 학습에 사용하는 데이터의 샘플링 비율. 기본값은 1이며, 이는 전체 학습 데이터를 기반으로 학습한다는 의미. (0.5일 경우 학습 데이터의 50%).
▶ 과적합이 염려될 경우, 1보다 작은 값으로 설정.
다음 내용
GBM 기반 ML 패키지인 XGBoost와 LightGBM
[머신러닝] 분류 - 앙상블 4 : XG Boost (1)
시작에 앞서해당 내용은 ' 권철민 지음. 위키북스' 를 토대로 작성되었습니다. 보다 자세한 내용은 해당 서적에 상세히 나와있으니 서적을 참고해 주시기 바랍니다.앙상블 학습(Ensemble Learning) [
puppy-foot-it.tistory.com
[출처]
파이썬 머신러닝 완벽 가이드
핸즈 온 머신러닝
'[파이썬 Projects] > <파이썬 머신러닝>' 카테고리의 다른 글
| [머신러닝] 앙상블: XG Boost (2) (0) | 2024.07.01 |
|---|---|
| [머신러닝] 앙상블 : XG Boost (1) (0) | 2024.07.01 |
| [머신러닝] 앙상블 : 랜덤 포레스트 (0) | 2024.06.27 |
| [머신러닝] 앙상블 학습(Ensemble Learning) (0) | 2024.06.27 |
| [머신러닝] 결정트리 - 사용자 행동 인식 데이터 세트 (0) | 2024.06.23 |



