이전 내용
[개발자를 위한 수학] 선형회귀 - 1
선형 회귀(linear regression) 데이터 과학과 통계학의 핵심인 선형 회귀는 관측 데이터에 맞는 직선을 훈련하고, 이를 통해 변수 간의 선형 관계를 보여주고 새로운 데이터에 대한 예측을 만든다.
puppy-foot-it.tistory.com
과대적합 및 분산
선형 회귀 외에 제곱 합의 값이 0이 되도록 손실을 최소화하는 방법 중 하나는 단순히 모든 포인트를 지나는 곡선을 찾는 것이다. 포인트 사이를 연결하여 회귀를 수행하면 손실은 0이 된다.
그러나 이런 포인트 연결 모델은 심하게 과대적합(overfitting) 되었는데, 즉 훈련 데이터에만 너무 정확하게 맞아서 새로운 데이터에 대해 제대로 예측하지 못한다.
이 모델은 다른 데이터에서 멀리 떨어져 있는 이상치에 민감하므로 예측의 분산이 높다. 즉, 과대적합은 예측의 분산을 증가시키기 때문에 엉뚱한 예측 결과가 생긴다. 이 때문에 머신러닝 모델에 편향을 추가하는 것이다.
모델의 편향은 데이터의 내용을 정확히 맞추는 대신, 특정 방법에 우선순위를 두는 것을 의미한다.
편향된 모델은 훈련 데이터의 손실을 최소화하는 대신, 약간의 여지를 남겨 새로운 데이터에서 손실을 최소화해 더 나은 예측을 만들기를 기대한다.
모델에 편향을 추가하는 것은 과대적합을 과소적합(underfitting)으로 상쇄하거나 훈련 데이터에 덜 맞추는 것이다.
[선형 회귀의 인기 있는 두 가지 변형]
- 릿지 회귀: 선형 회귀에 페널티 형태로 편향을 추가해 데이터에 덜 잘 맞도록 만듦.
- 라쏘 회귀: 잡음이 많은 변수를 구분해내므로 관련성이 없는 변수를 자동으로 제거하고자 할 때 유용.
단, 선형 회귀는 단순하지만 입력 변수가 많으면 쉽게 과대적합 될 수 있기 때문에 과대적합과 과소적합을 모두 확인하고 둘 사이에 있는 최적의 지점을 찾아야 한다. 만약 이런 지점이 없다면 모델을 포기해야 한다.
확률적 경사 하강법
머신러닝 작업에서는 한 번에 모든 훈련 데이터를 사용해 훈련하지 않고, (배치 경사 하강법)
실제로는 각 반복마다 데이터셋에 있는 표본 하나만 사용해 훈련하는 확률적 경사 하강법을 수행할 확률이 높다.
※ 미니배치 경사 하강법: 각 반복마다 데이터셋에 있는 여러 개의 표본을 사용.
[각 반복에서 데이터의 일부만 사용하는 이유]
- 각 반복이 전체 훈련 데이터셋을 처리할 필요 없이 일부만 처리하기 때문에 계산량이 크게 줄어듦.
- 과대적합을 줄임. 각 반복에서 훈련 알고리즘을 데이터의 일부에만 노출하면 손실 지형이 계속 바뀌므로 최솟값에 안주하지 않는다. (약간의 무작위성을 도입해 과소적합을 조금 주입)
▶ 근삿값이 부정확해지는 것을 주의하여 훈련/테스트 데이터 분할과 선형 회귀의 신뢰성을 평가하기 위한 다른 측정 지표 도입
[선형 회귀를 위한 확률적 경사 하강법 수행]
# 선형 회귀를 위한 확률적 경사 하강법 수행
import pandas as pd
import numpy as np
# 데이터 로드
data = pd.read_csv('http://bit.ly/2KF29Bd', header=0)
X = data.iloc[:, 0].values
Y = data.iloc[:, 1].values
n = data.shape[0] # 행
# 계수 초기화
m = 0.0
b = 0.0
sample_size = 1 # 표본 크기
L = .0001 # 학습률
epochs = 1000000 # 경사 하강법을 수행할 반복 횟수
# 확률적 경사 하강법 수행
for i in range(epochs):
idx = np.random.choice(n, sample_size, replace=False)
x_sample = X[idx]
y_sample = Y[idx]
# 예측한 Y 값
Y_pred = m * x_sample + b
# m에 대한 그레이디언트
D_m = (-2 / sample_size) * sum(x_sample * (y_sample - Y_pred))
# b에 대한 그레이디언트
D_b = (-2 / sample_size) * sum(y_sample - Y_pred)
# m과 b 업데이트
m = m - L * D_m
b = b - L * D_b
# 진행 과정 출력
if i % 10000 == 0:
print(i, m, b)
print("y = {0}x + {1}".format(m, b))
상관 계수 (또는 피어슨 상관 계수)
상관 계수는 두 변수 사이의 관계 강도를 -1에서 1 사이의 값으로 측정하며, 상관 계수가 0에 가까울수록 상관관계가 없음을 나타낸다. 상관 계수가 1에 가까울수록 강한 양의 상관관계를 나타내며 이는 한 변수가 증가하면 다른 변수도 비례적으로 증가한다는 의미이다. 상관 계수가 -1에 가까우면 강한 음의 상관관계를 나타내며 이는 한 변수가 증가하면 다른 변수도 비례적으로 감소함을 의미한다.
[상관 관계, 산포도 등의 개념]
[빅데이터 분석기사] 2과목 빅데이터 탐색(2-1-1)
[목차] [빅데이터 분석기사] 시험 과목 및 주요 내용 (필기)빅데이터 분석기사 (필기) 시험 과목 및 주요 내용 출처: 데이터자격검정 (dataq.or.kr) 필기과목명 주요항목 세부항목 세세항목 빅데이터
puppy-foot-it.tistory.com
상관 계수는 두 변수 사이에 가능한 관계가 있는지 확인하는 데 유용하며, 강한 양의 상관관계나 강한 음의 상관관계가 있는 경우 선형 회귀가 잘 맞는다. 만약 변수 사이에 상관관계가 없다면 모델에 잡음이 추가되고 정확도가 떨어진다.
파이썬으로 상관 계수를 계산하려면 판다스의 corr() 함수를 사용하면 되는데, 이 함수를 사용하면 데이터셋의 모든 변수 쌍 간의 상관 계수를 쉽게 확인할 수 있으며, 이를 상관 행렬(correlation matrix)라고 한다.
[판다스로 모든 변수 쌍 간의 상관 계수 확인하기]
# 판다스로 모든 변수 쌍 간의 상관 계수 확인하기
import pandas as pd
# 데이터 로드
df = pd.read_csv('http://bit.ly/2KF29Bd', delimiter=',')
# 변수 간의 상관 계수 출력
correlations = df.corr()
print(correlations)
▶ x와 y 사이의 상관 계수 0.957586 은 두 변수 간에 강한 양의 상관관계가 있음을 나타낸다.
분산이 많은 데이터셋을 사용하면 상관 계수가 감소하는데, 이는 상관관계가 약해졌음을 의미한다.
※ delimiter
구분 문자(delimiter)는 일반 텍스트 또는 데이터 스트림에서 별도의 독립적 영역 사이의 경계를 지정하는 데 사용하는 하나의 문자 혹은 문자들의 배열을 말한다.
통계적 유의성
선형 회귀에서 고려해야 할 또 다른 측면은 데이터에 있는 상관관계가 우연인지의 여부를 살펴봐야 한다는 것이다.
가설 검정과 p 값을 활용해 선형 회귀에 적용해본다.

[가설 검정]
[개발자를 위한 수학] 추론통계: 가설 검정 (+파이썬)
이전 내용 [개발자를 위한 수학] 추론 통계추론 통계 추론 통계는 모집단에 대한 어떤 미지의 양상을 알기 위해 통계학을 이용하여 추측하는 과정을 지칭한다. 추론 통계에서는 표본과 모집단
puppy-foot-it.tistory.com
★ 통계 분석에 관심이 있을 경우, statsmodel 라이브러리를 활용하면 좋다.
이 라이브러리는 사이킷런이나 다른 머신러닝 라이브러리에서 제공하지 않는 통계적 유의성 및 신뢰 구간을 위한 도구를 제공한다.
statsmodels 0.14.4
statsmodels is a Python module that provides classes and functions for the estimation of many different statistical models, as well as for conducting statistical tests, and statistical data exploration. An extensive list of result statistics are available
www.statsmodels.org
앞선 데이터셋의 상관 계수를 계산한 결과는 강력한 양의 상관관계를 나타낸다.
그러나 이것이 우연에 의한 것인지 평가해야 하는데, 이 두 변수 간에 관계가 있는지 알아보기 위해 양측 검정을 사용해 95% 신뢰도로 가설 검정을 수행해 본다. (양측 검정, 신뢰도 등의 내용 역시 상단의 링크를 확인해보면 알 수 있다.)
# t 분포에서 임곗값 계산하기
from scipy.stats import t
n = 10
lower_cv = t(n-1).ppf(.025)
upper_cv = t(n-1).ppf(.975)
print(lower_cv, upper_cv)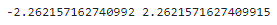
▶ 선형 회귀를 통해 가설 검증을 할 때는 정규 분포가 아닌 t 분포를 사용한다.
표본에 10개의 데이터가 있으므로 자유도(n)는 10-1=9 이다.
임곗값은 ± 2.262 이며, 테스트 값이 이 범위를 벗어나면 귀무 가설을 거부할 수 있다.
[선형으로 보이는 데이터에 대한 유의성 테스트]
# 선형으로 보이는 데이터에 대한 유의성 테스트
from scipy.stats import t
from math import sqrt
# 표본 크기
n = 10
lower_cv = t(n-1).ppf(.025)
upper_cv = t(n-1).ppf(.975)
# 데이터에서 계산한 결정 계수
r = 0.95758
# 검정 수행
test_value = r / sqrt((1-r**2) / (n-2))
print('검정값: {}'.format(test_value))
print('임계 범위: {}'.format(lower_cv, upper_cv))
if test_value < lower_cv or test_value > upper_cv:
print('상관관계가 입증되어 귀무 가설 거부')
else:
print('상관관계가 입증되지 않아 귀무 가설을 거부하지 못함')
# p 값 계산
if test_value > 0:
p_value = 1.0 - t(n-1).cdf(test_value)
else:
p_value = t(n-1).cdf(test_value)
# 양측 검정이므로 2를 곱함
p_value = p_value * 2
print('P-VALUE: {}'.format(p_value))
▶ 테스트 값은 약 9.3988 로, 임계 범위를 벗어나므로 귀무 가설을 거부하고 상관관계가 있다고 할 수 있다.
p 값 0.00000598은 확실히 유의미하여 임곗값인 0.05보다 훨씬 낮기 때문에 우연이 아니라 상관관계가 있다고 본다.
결정 계수(coefficient of determination)
결정 계수는 한 변수의 변동이 다른 변수의 변동으로 얼마나 설명 가능한지를 측정하며, 상관 계수 r의 제곱이기도 하다.
r이 완벽한 상관관계 (1 또는 -1) 에 가까워지면 결정 계수는 1에 가까워진다.
[판다스에서 결정 계수 계산하기]
# 판다스에서 결정 계수 계산하기
import pandas as pd
# 데이터 로드
df = pd.read_csv('http://bit.ly/2KF29Bd', delimiter=',')
# 두 변수 사이의 결정 계수 출력
coeff_determination = df.corr(method='pearson') **2
print(coeff_determination)
▶ 결정 계수 0.916971은 x의 변동 중 91.6971%가 y에 의해 설명된다는 뜻이며, 나머지 8.3029%는 포착되지 않은 다른 변수로 인한 잡음으로 해석한다.
상관관계는 인과관계와 같지 않으므로 겉으로 보이는 관계에 기여하는 다른 변수가 있을 수 있다.
다음 내용
[개발자를 위한 수학] 선형 회귀 - 3
이전 내용 [개발자를 위한 수학] 선형 회귀 - 2이전 내용 [개발자를 위한 수학] 선형회귀 - 1선형 회귀(linear regression) 데이터 과학과 통계학의 핵심인 선형 회귀는 관측 데이터에 맞는 직선을 훈
puppy-foot-it.tistory.com
[출처]
개발자를 위한 필수 수학
위키백과
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.9)-1 (2) | 2024.10.17 |
|---|---|
| [개발자를 위한 수학] 선형 회귀 - 3 (7) | 2024.10.17 |
| [개발자를 위한 수학] 선형회귀 - 1 (8) | 2024.10.16 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.8)-3 (4) | 2024.10.13 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.8)-2 (1) | 2024.10.13 |



