★ 시작에 앞서 ★
해당 내용은 '<현대통계학-제6판>, 다산출판사, 2024' 에 나와있는 챕터별 연습문제를 교재를 응용하여 풀이하고, 수학적인 문제에 대한 답변을 파이썬으로 구현해보기 위해 작성하는 글이다.
해당 답변을 구현하는 방식은 답안지 없이 필자가 스스로 구현하는 것이므로, 정확한 (혹은 가장 효과적인) 답변이 아닐 수 있다. 이 글의 목적은 통계학 공부와 파이썬 프로그래밍 언어 공부를 동시에 하고자 함이며, 통계학을 공부하고 싶으신 분들은 해당 교재를 구매하는 것을 추천한다.
또한, 연습문제 번호 및 문제 내용은 필자가 임의대로 작성하였으며, 교재와는 다를 수 있다.
잘못된 부분이 있다면 언제든 피드백 부탁 드립니다! 감사합니다
챕터 9 주요 개념
[추론통계학]
모집단 전체를 분석하는 것은 시간적, 경제적 제약 등으로 어려울 수 있으므로, 표본의 특성을 나타내는 통계량을 계산한 다음 이를 기초로 하여 모집단의 모수를 찾아내야 한다. 따라서 가능한 한 모수를 정확하게 추정하는 것이 통게적 분석에서 가장 중요한데, 이 모수를 정확하게 추정하는 분야를 다루는 통계학을 추론통계학이라 한다.
- 추론 통계학이 다루는 영역
- 통계적 추정(statistical estimation): 표본의 성격을 나타내는 통계량을 기초로 하여 모수를 추정하는 통계적 분석 방법
- 가설검정(hypothesis test): 모수에 대하여 특정한 가설을 세워 놓고, 표본을 선택하여 통계량을 계산한 다음, 이를 기초로 하여 모수에 대한 가설의 진위를 판단하는 방법.
◆ 점추정: 하나의 값으로 모숫값을 추정하는 방법. 표본으로부터 구할 수 있는 통계량 가운데 모수를 추정하기에 가장 적절한 것을 결정하여 그 값을 모숫값으로 보는 것.
단점▶ 추정에 있어서 불확실성의 정도를 표현하지 못함.
- 추정값(estimate): 모수를 추정하여 나온 결괏값
- 추정량(estimator): 추정값을 구하기 위하여 사용되는 추정방법 또는 추정값 계산을 위한 통계량
추정량의 기댓값이 추정할 모수의 실젯값과 일치하거나 또는 그 값에 가까이 갈수록 바람직한 추정량이라고 할 수 있다.
점추정에서 모수를 추정하는 데 무엇을 추정량으로 삼느냐가 매우 중요하다.
<적절한 추정량을 선택하는 4가지 기준>
- 불편성(unbiasedness): 추정량의 기댓값이 실제 모수의 값과 차이가 나면 그 추정량은 편의를 갖는다고 하며, 추정량이 0의 편의를 가지는 것.
- 효율성(efficiency): 추정량 중에서 최소의 분산을 가진 추정량
- 일치성(consistency): 표본의 크기 n이 무한히 증가함에 따라 추정량이 모수에 가까워지는 것. (표본의 크기가 커지면 커질수록 추정량과 모수 간의 차이가 차차 작아지게 되는 것)
- 충분성(sufficiency): 추정량이 모수에 대하여 가장 많은 정보를 제공할 때, 그 추정량은 충분성이 있다고 한다.
▶ 선택된 추정량이 위의 네 가지 조건을 모두 충족시키지 못할 경우엔 첫째 조건인 불편성에 가장 큰 비중을 두어 적절한 추정량을 선택해야 한다.
◆ 구간 추정: 적절한 구간을 가지고 모수를 추정하는 것.표본의 통계량을 기초로 모수가 존재할 일정구간 (신뢰구간)을 추정하는 방법으로 점추정에 비하여 더 많이 사용되는 통계적 추정 방법이다.
장점 - 모수가 존재할 범위를 제공함으로써 연구자가 원하는 만큼의 정확도를 가지고 모수를 추정할 수 있다.
[정규분포 모집단의 표준편차 𝜎 를 알고 있을 경우 신뢰구간 추정]
- z 값에 대한 신뢰구간

- 𝜇 값에 대한 신뢰구간
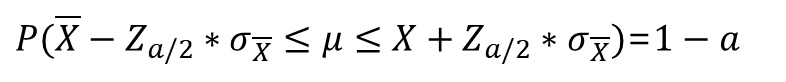
위의 식들에서 '1-a'는 신뢰도(confidence level) 또는 신뢰수준이라고 한다.
신뢰도는 이와 같이 구간으로 추정된 추정값이 실제 모집단의 모수를 포함하고 있을 가능성을 말하며, 이때 모수가 포함될 것으로 추정된 구간을 신뢰구간(confidence interval)이라 한다.
신뢰구간은 신뢰도에 따라서 필요한 Za/2 값을 정하여 추정하는데, Z-분포표를 이용하여 이에 대응하는 Za/2 값을 찾으면 된다.
- 신뢰도에 따른 Za/2 값
| 신뢰도(1-a) | Z=0에서 Za/2 까지 면적 | Za/2 |
| 0.90 (90%) | 0.450 | 1.64 |
| 0.95 (95%) | 0.475 | 1.96 |
| 0.99 (99%) | 0.495 | 2.57 |
[정규분포 모집단의 표준편차 𝜎 를 모르는 있을 경우 신뢰구간 추정]
모집단의 표준편차를 모를 때에는 표본에서 구한 불편추정량 S, 즉 표본의 표준편차를 모집단의 표준편차 대신으로 사용한다.

또한, 이 통계량은 t-분포를 이용하여 신뢰구간을 구해야 하며, 이때의 표본통계량을 t-통계량이라 한다.
★ t-분포
t-곡선의 모양을 결정하는 것은 자유도(degrees of freedom, df) 이며, 표본의 크기 n에서 1을 뺀 값이다.
자유도란 자료집단의 관찰값 중에서 자유롭게 선택될 수 있는 관찰값의 수를 말한다.
- t-분포에서의 신뢰구간
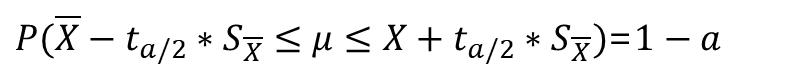
표본의 크기가 클 때 (30 이상)에는 표본의 표준편차와 모집단의 표준편차의 차이가 작기 때문에 t-분포 대신 Z-분포를 사용하여도 무방하다.
[모집단 평균을 추정할 대 표본크기의 결정]
표본크기는 다음과 같은 요인들과 관련되어 있다.
- 신뢰구간: 오차의 크기와 표준편차가 정해졌을 때, 신뢰구간을 크게 할수록 표본의 크기를 크게 해야 한다.
- 표준편차: 오차의 크기와 신뢰구간이 정해졌을 때, 표준편차 또는 분산이 클수록 표본의 크기도 커야 한다.
- 오차의 크기: 신뢰구간과 표준편차가 정해졌을 때, 오차를 작게 하기를 원하면 표본의 크기는 커야 한다.
[모집단 비율을 추정할 때 표본크기의 결정]
모집단 비율의 신뢰구간을 추정할 때에도 일정한 신뢰도에서 허용가능한 오차를 가져올 최소한의 표본크기를 계산할 수 있다.
보수적으로 𝜎_𝑝 가 최대인 값, 즉 𝜋=0.5일 때의 𝜎_𝑝 값으로 표본의 크기 n 을 정하는 것이 가장 안전하다.

챕터9 예제 1 및 파이썬 풀이
Q. 우리나라 대학생들의 월평균 용돈이 얼마인지 알아보려고 한다. 100명을 임의로 선택한 결과, 그들의 평균이 582,000원 이라는 것을 알았다. 모집단의 표준편차가 10만 원이고, 모집단이 정규분포를 이룬다고 가정했을 때 우리나라 대학생들 평균 용돈의 90% 신뢰구간, 95% 신뢰구간, 99% 신뢰구간을 구하여 보자.
# 대학생 월평균 용돈 신뢰구간
import numpy as np
import scipy.stats as stats
# 주어진 데이터
mean = 582000 # 표본 평균
std_dev = 100000 # 모집단 표준편차
n = 100 # 표본 크기
# 신뢰수준 설정
confidence_levels = [0.90, 0.95, 0.99]
# 결과 출력
for confidence in confidence_levels:
# Z 값 계산 (신뢰구간의 양 끝에서 Z값을 계산)
z_score = stats.norm.ppf(1 - (1 - confidence) / 2)
# 신뢰구간 계산
margin_of_error = z_score * (std_dev / np.sqrt(n))
confidence_interval = (mean - margin_of_error, mean + margin_of_error)
# 출력
print(f"{int(confidence * 100)}% 신뢰구간: {confidence_interval[0]:,.0f}원 ~ {confidence_interval[1]:,.0f}원")
챕터9 예제 2 및 파이썬 풀이
Q. 달성중학교 학생 1,000명의 평균 통학거리를 알아보려고 한다. 모든 학생을 대상으로 조사하는 것은 어려우므로, 16명을 임의로 뽑아 조사해 본 결과 그들의 평균 통학거리는 1,640m이며, 표본에서 계산된 표준편차는 2,000m 였다. 통학거리의 분포가 정규분포라고 가정한다면, 이 학교 학생들의 평균 통학거리의 90% 신뢰구간을 구하라.
# 달성중학교 학생 평균 통학거리
import numpy as np
from scipy.stats import t
# 주어진 데이터
mean = 1640
s = 2000 # 표본 표준편차
n = 16 # 표본 크기
# 신뢰수준 설정
confidence_level = 0.90
# t값 계산
t_score = t.ppf(1 - (1 - confidence_level) / 2, df=n-1)
# 신뢰구간 계산
margin_of_error = t_score * (s / np.sqrt(n))
confidence_interval = (mean - margin_of_error, mean + margin_of_error)
# 출력
print(f"{int(confidence_level * 100)}% 신뢰구간: {confidence_interval[0]:,.0f}m ~ {confidence_interval[1]:,.0f}m")
챕터9 예제 3 및 파이썬 풀이
Q. 전기자동차를 생산하는 트윈산업에서 하루 평균 전기자동차 생산량을 조사하려고 한다. 과거 121일 간의 하루 생산량의 평균과 표준편차를 계산하였더니 평균 500대, 표준편차는 110대 였다. 평균 생산량에 대하여 90% 신뢰구간을 t-분포와 Z-분포를 이용하여 각각 구하라.
# 전기 자동차 평균 생산량
import numpy as np
from scipy.stats import t
import scipy.stats as stats
# 주어진 데이터
mean = 500
s = 110
n = 121
# 신뢰수준 설정
confidence_level = 0.90
# Z 값 계산 (신뢰구간의 양 끝에서 Z값을 계산)
z_score = stats.norm.ppf(1 - (1 - confidence_level) / 2)
# t값 계산
t_score = t.ppf(1 - (1 - confidence_level) / 2, df=n-1)
# 신뢰구간 계산
margin_of_error_z = z_score * (s / np.sqrt(n)) # z 값에 대한 신뢰구간
margin_of_error_t = t_score * (s / np.sqrt(n)) # t 값에 대한 신뢰구간
confidence_interval_z = (mean - margin_of_error_z, mean + margin_of_error_z)
confidence_interval_t = (mean - margin_of_error_t, mean + margin_of_error_t)
# 출력
print(f"Z값{int(confidence_level * 100)}% 신뢰구간: {confidence_interval_z[0]:,.2f}대 ~ {confidence_interval_z[1]:,.2f}대")
print(f"t값{int(confidence_level * 100)}% 신뢰구간: {confidence_interval_t[0]:,.2f}대 ~ {confidence_interval_t[1]:,.2f}대")
챕터9 예제 4 및 파이썬 풀이
Q. 한 연구자는 서울 시민의 공유자전거 이용 현황을 파악하고자 한다. 이를 조사하기 위하여 서울 시민 10,000명을 임의로 뽑아 조사한 결과, 이 중 6,200명이 공유자전거 이용 경험이 있다고 답했다. 서울 시민 중 공유자전거를 이용해 본 이들의 비율은 어느정도인가? 99%의 신뢰구간을 구하라.
# 서울 시민 공유자전거 이용 비율
import numpy as np
import scipy.stats as stats
used = 6200 # 자전거 이용 경험 인원
total = 10000 # 조사 대상 전체 인원 수
# 표본 비율
p = used / total
# 표본 표준 편차
Sp = ((p * (1 - p)) / total) ** 0.5
# 신뢰 수준 설정
confidence_level = 0.99
# z 값 계산
z_score = stats.norm.ppf(1 - (1 - confidence_level) / 2)
# 신뢰구간 계산
margin_of_error = z_score * Sp
confidence_interval = (p - margin_of_error, p + margin_of_error)
# 출력
print(f'표본 비율: {p:.2f}')
print(f'표본 표준 편차: {Sp:.5f}')
print(f'Z값: {z_score:.2f}')
print(f"{int(confidence_level * 100)}% 신뢰구간: {confidence_interval[0]:,.3f} ~ {confidence_interval[1]:,.3f}")
모집단 비율을 알지 못하는 경우에는 표본비율을 사용하여 표본표준편차를 표집분포의 표준편차에 대한 추정량으로 사용한다.

이때 n이 충분히 크다면 (30 이상) 표본비율에 해당하는 Z 값은 아래와 같다.

실제의 경우 표집분포의 표준편차를 모르는 경우가 대부분이므로, 표본표준편차를 이용하여 모집단 비율에 대한 신뢰 구간을 추정하게 되며, 모집단 비율 𝜋의 신뢰구간을 구하는 공식은 아래와 같다.
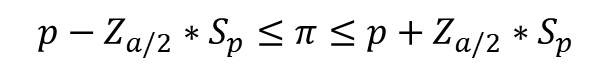
챕터9 예제 5 및 파이썬 풀이
Q. 어느 음료수제조회사에서는 16온스 용량의 에너지드링크를 생산하고 있다. 실제 무게가 그러한가를 알아보기 위해 표본을 뽑으려고 한다. 모집단 평균 무게에 대한 추정값의 오차가 0.2 온스 이상이 되지 않을 것을 원하며, 이 결과가 99%의 신뢰도를 갖기를 바란다. 지금까지의 경험으로 𝜎=1.34 라는 것을 알고 있을 때, 이러한 요구를 충족시키기 위하여 표본크기를 얼마로 해야 하는가?
# 음료수 제조 회사
import numpy as np
import scipy.stats as stats
# 신뢰 수준 설정
confidence_level = 0.99
# z 값 계산
z_score = stats.norm.ppf(1 - (1 - confidence_level) / 2)
# 표준 편차
s = 1.34
# 오차의 크기
e = 0.2
# 표본크기
n = ((z_score * s) / e) **2
print(f'표본크기: {n:.0f}')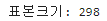
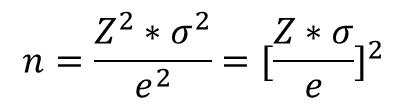
챕터9 예제 6 및 파이썬 풀이
Q. 정부는 저소득층 가정을 대상으로 의료혜택을 받지 못하고 있는 가정의 비율을 조사하려고 한다. 99%의 신뢰도를 가지고 추정할 때 허용할 수 있는 최대의 오차를 0.05로 한다면 표본의 크기는 얼마가 되어야 하나?
# 저소득층 가정 조사
import numpy as np
import scipy.stats as stats
# 신뢰 수준 설정
confidence_level = 0.99
# z 값 계산
z_score = stats.norm.ppf(1 - (1 - confidence_level) / 2)
# 오차의 크기
e = 0.05
# 표본크기
n = ((z_score ** 2) /(4 * (e **2)))
print(f'표본크기: {n:.0f}')
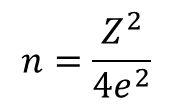
다음 내용
[파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.9)-2
★ 시작에 앞서 ★ 해당 내용은 ', 다산출판사, 2024' 에 나와있는 챕터별 연습문제를 교재를 응용하여 풀이하고, 수학적인 문제에 대한 답변을 파이썬으로 구현해보기 위해 작성하는 글이다.해
puppy-foot-it.tistory.com
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [개발자를 위한 수학] 로지스틱 회귀와 분류 - 1 (3) | 2024.10.18 |
|---|---|
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.9)-2 (6) | 2024.10.18 |
| [개발자를 위한 수학] 선형 회귀 - 3 (7) | 2024.10.17 |
| [개발자를 위한 수학] 선형 회귀 - 2 (3) | 2024.10.16 |
| [개발자를 위한 수학] 선형회귀 - 1 (8) | 2024.10.16 |



