이전 내용
[개발자를 위한 수학] 선형 회귀 - 2
이전 내용 [개발자를 위한 수학] 선형회귀 - 1선형 회귀(linear regression) 데이터 과학과 통계학의 핵심인 선형 회귀는 관측 데이터에 맞는 직선을 훈련하고, 이를 통해 변수 간의 선형 관계를 보
puppy-foot-it.tistory.com
추정 표준 오차
- 제곱 오차 합(Sum of squared error, SSE): 잔차를 제곱하고 합산하는 방식으로 선형 회귀의 전체 오차를 측정하는 방법.

- 추정 평균 오차(Standard error of the estimate): 제곱한 값을 제곱근을 사용해 원래 단위로 다시 조정한 뒤, 이 값을 평균한 값.

★ n - 2 를 사용하는 것은, 단순 선형 회귀에는 변수가 하나가 아니라 두 개 이기 때문에 자유도에서 불확실성을 하나 더 증가시켜야 하기 때문이다.
[파이썬으로 추정 표준 오차 계산하기]
# 추정 표준 오차 계산
import pandas as pd
from math import sqrt
# 데이터 로드
points = list(pd.read_csv('http://bit.ly/2KF29Bd', delimiter=',').itertuples())
n = len(points)
# 모델 파라미터 초기화
m = 1.939
b = 4.733
# 추정 표준 오차 계산
S_e = sqrt((sum((p.y - (m*p.x + b))**2 for p in points))/(n-2))
print(S_e)
예측 구간(prediction interval)
선형 회귀를 사용하면 데이터가 선형적인 방식으로 정규 분포를 따르기를 바란다. 회귀 직선은 종 곡선의 변화하는 '평균' 역할을 하며, 직선 주위에 퍼진 데이터는 분산과 표준 편차를 반영한다.
선형 회귀 직선을 따르는 정규 분포가 있는 경우, 하나의 변수뿐만 아니라 분포를 조정하는 두 번째 변수도 있다. 각각의 y 예측 주위에 신뢰 구간이 있으며 이를 예측 구간이라고 한다.
이 예측 구간은 오차 범위를 구하고 예측된 y 값을 중심으로 오차 범위를 더하거나 빼는 방식으로 계산하는데, 이는 추정 오차 뿐만 아니라 t 분포의 임곗값을 포함하는 매우 복잡한 방정식이며, 이를 파이썬으로 계산하는 방식은 아래와 같다.
[예시를 이용한 예측 구간 계산 방법]
예시: 반려동물의 나이와 동물병원 방문 횟수 데이터
- 8.5살인 강아지가 동물병원에 방문하는 예측 구간 계산하기
# 8.5살인 강아지가 동물병원에 방문하는 예측 구간 계산하기
import pandas as pd
from math import sqrt
from scipy.stats import t
# 데이터 로드
points = list(pd.read_csv('http://bit.ly/2KF29Bd', delimiter=',').itertuples())
n = len(points)
# 모델 파라미터 초기화
m = 1.939
b = 4.733
# x=8.5에 대한 예측 구간 계산
x_0 = 8.5
x_mean = sum(p.x for p in points) / n
t_value = t(n -2).ppf(.975)
S_e = sqrt((sum((p.y - (m*p.x + b))**2 for p in points))/(n-2))
margin_of_error = t_value * S_e * sqrt(1 + (1 / n) + (n * (x_0 - x_mean) **2) / (n * sum(p.x ** 2 for p in points) - sum(p.x for p in points) ** 2))
predicted_y = m * x_0 + b
# 예측 구간 계산
print(predicted_y - margin_of_error, predicted_y + margin_of_error)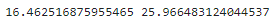
▶ 8.5살인 강아지는 동물 병원을 16.46 ~ 25.96번 방문할 확률이 95% 라는 예측이 가능하다.
(단일 값이 아닌 범위를 사용해 불확실성을 설명하기 때문에 훨씬 더 안전한 주장이 된다)
훈련/테스트 분할
- 훈련/테스트 분할: 머신러닝 실무자가 과대적합을 완화하기 위해 사용하는 기본 방법. 이 기법은 일반적으로 로지스틱 회귀 및 신경망을 포함한 모든 지도 학습에 사용된다.
일반적으로 1/3은 테스트용으로, 나머지 2/3은 훈련용으로 사용한다. 물론, 비율을 다르게 사용할 수도 있다.
시간이 촉박하거나 데이터가 너무 방대해 통계적으로 분석할 수 없는 경우, 훈련/테스트 분할은 이전에 본 적 없는 데이터에서 선형 회귀가 얼마나 잘 수행되는지 측정할 수 있는 방법이다.
- 훈련 데이터셋: 선형 회귀 모델을 훈련용 (비율: 2/3)
- 테스트 데이터셋; 이전에 본 적이 없는 데이터에 대한 선형 회귀 모델의 성능 측정용 (비율: 1/3)
★ 훈련/테스트 데이터셋을 분할하는 다른 방법들
- 교차 검증: 1/3 씩 테스트 데이터셋을 번갈아 사용 (3-폴드 교차 검증)
- k-폴드 교차 검증(k-fold cross validation)
- 훈련 9/10, 테스트 1/10의 비율로 사용
- LOOCV(leave-one-out cross-validation): 각각의 데이터 포인트 하나를 테스트 데이터셋으로 사용(전체 데이터셋이 작을 때 유용)
[사이킷런으로 훈련/테스트 분할 수행]
#사이킷런으로 훈련/테스트 분할 수행
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 데이터 로드
df = pd.read_csv('https://bit.ly/3cIH97A', delimiter=',')
# (마지막 열 제외) 모든 열을 입력 변수로 추출
X = df.values[:, :-1]
# 마지막 열을 출력으로 추출
Y = df.values[:, -1]
# 훈련 데이터와 테스트 데이터 분할 (테스트용은 1/3)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size =1/3)
model = LinearRegression() # 선형 회귀
model.fit(X_train, Y_train)
result = model.score(X_test, Y_test)
print("결정 계수: %.3f" % result)
<코드 설명>
- train_test_split(): 데이터셋(X 및 Y열)을 받아 섞은 다음, 테스트 데이터셋 크기에 따라 훈련 및 테스트 데이터셋을 나누어 반환
- model.fit(X_train, Y_train): LinearRegression의 fit() 메서드로 훈련 데이터셋 X_train과 Y_train 을 사용해 훈련
- score(X_test, Y_test) : score() 메서드로 테스트 데이터셋 X_test와 Y_test를 사용해 결정계수 (r^2) 계산
▶ 이전에 본 적 없는 데이터에서 회귀 모델의 성능 측정 가능하며, 결정계수 값이 높을수록 회귀 모델이 이전에 본 적 없는 데이터에 대해 잘 수행된다는 것을 나타낸다.
1.0에 가까울수록 훈련 데이터와 상관 관계가 강하며,
0.0에 가까울수록 테스트 데이터셋의 성능이 좋지 않다.
◆ 교차검증을 사용한 측정
1) 3-폴드 교차 검증: 전체 데이터셋을 1/3씩 나누어(3개의 폴드로) 번갈아 가며 테스트 데이터셋으로 사용하는 방법
★ 폴드: 교차 검증에서 각 분할
[선형 회귀에 3-폴드 교차 검증 사용하기]
# 선형 회귀에 3-폴드 교차 검증 사용하기
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import KFold, cross_val_score
# 데이터 로드
df = pd.read_csv('https://bit.ly/3cIH97A', delimiter=',')
# (마지막 열 제외) 모든 열을 입력 변수로 추출
X = df.values[:, :-1]
# 마지막 열을 출력으로 추출
Y = df.values[:, -1]
# 단순 선형 회귀 수행
kfold = KFold(n_splits=3, random_state=7, shuffle=True)
model = LinearRegression()
results = cross_val_score(model, X, Y, cv=kfold)
print(results)
print("MSE: 평균={:.3f} (표준 편차={:.5f})".format(results.mean(), results.std()))
2) 랜덤 폴드 교차 검증(random-fold cross validation)
모델의 분산이 우려되는 경우, 간단한 훈련/테스트 분할 또는 교차 검증 대신 랜덤 폴드 교차 검증을 사용할 수 있다. 이는 데이터를 여러 번 반복해 섞어 훈련/테스트 분할을 진행하고 테스트 결과를 집계하는 방법이다.
아래의 예시는 데이터의 1/3을 테스트용으로, 나머지 2/3을 훈련용으로 무작위하게 샘플링하는 작업을 10회 반복한 뒤, 이 10개의 테스트 결과와 표준 편차를 평균 내어 테스트 데이터셋에서 얼마나 일관되게 수행되는지 확인한다.
이때는 회귀 모델을 여러 번 훈련하기 때문에 계산 비용이 많이 발생된다는 문제가 있다.
[선형 회귀에 랜덤 폴드 교차 검증 사용하기]
# 선형 회귀에 랜덤 폴드 교차 검증 사용하기
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score, ShuffleSplit
# 데이터 로드
df = pd.read_csv('https://bit.ly/38XwbeB', delimiter=',')
# (마지막 열 제외) 모든 열을 입력 변수로 추출
X = df.values[:, :-1]
# 마지막 열을 출력으로 추출
Y = df.values[:, -1]
# 단순 선형 회귀 수행
kfold = ShuffleSplit(n_splits=10, test_size=.33, random_state=7)
model = LinearRegression()
results = cross_val_score(model, X, Y, cv=kfold)
print(results)
print("MSE: 평균={:.3f} (표준 편차={:.5f})".format(results.mean(), results.std()))
다중 선형 회귀
모델이 변수로 넘쳐나 설명력을 잃기 시작하면 불안정해진다. 이때부터 모델을 블랙박스로 취급하기 시작하기 때문에 변수를 추가할수록 데이터는 점점 더 희소해진다는 사실을 기억해야 한다.
단순 선형 회귀(하나의 입력 변수, 하나의 출력 변수)를 수행하는 개념 및 방법은 대부분 다변수(multivariable) 선형 회귀에도 적용할 수 있다. 결정 계수, 표준 오차 및 신뢰 구간과 같은 지표를 사용할 수 있지만 변수가 많을수록 더 어려워진다.
[두 개의 입력 변수가 있는 선형 회귀 분석]
# 두 개의 입력 변수가 있는 선형 회귀 분석 (다중 회귀 분석)
import pandas as pd
from sklearn.linear_model import LinearRegression
# 데이터 로드
df = pd.read_csv('https://bit.ly/2X1HWH7', delimiter=',')
# (마지막 열 제외) 모든 열을 입력 변수로 추출
X = df.values[:, :-1]
# 마지막 열을 출력으로 추출
Y = df.values[:, -1]
# 모델 훈련
fit = LinearRegression().fit(X, Y)
# 파라미터 출력
print("계수= (0)".format(fit.coef_))
print("절편= {0}".format(fit.intercept_))
print("z = {0} + {1}x + {2}y".format(fit.intercept_, fit.coef_[0], fit.coef_[1]))
다음 내용
[개발자를 위한 수학] 로지스틱 회귀와 분류 - 1
로지스틱 회귀(logistic regression) 하나 이상의 독립 변수가 주어졌을 때 결과의 확률을 예측하는 알고리즘. 로지스틱은 선형 회귀와 유사하게 선형 방정식을 기반으로 하지만, 선형 회귀와는 달리
puppy-foot-it.tistory.com
[출처]
개발자를 위한 필수 수학
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.9)-2 (6) | 2024.10.18 |
|---|---|
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.9)-1 (2) | 2024.10.17 |
| [개발자를 위한 수학] 선형 회귀 - 2 (3) | 2024.10.16 |
| [개발자를 위한 수학] 선형회귀 - 1 (8) | 2024.10.16 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.8)-3 (4) | 2024.10.13 |



