로지스틱 회귀(logistic regression)
하나 이상의 독립 변수가 주어졌을 때 결과의 확률을 예측하는 알고리즘. 로지스틱은 선형 회귀와 유사하게 선형 방정식을 기반으로 하지만, 선형 회귀와는 달리 실수가 아닌 범주를 예측하는 분류 알고리즘이다. (회귀는 예측 결과가 실수인지 범주인지를 기준으로 구분 되며, 회귀는 실수, 분류는 범주로 구분 된다.)
로지스틱 회귀는 이산형 (이진수 1 또는 0) 또는 범주형(정수)인 출력 변수를 위해 훈련되며, 확률 형태의 연속형 값을 출력하지만 임곗값을 사용해 이산형 값으로 변환할 수 있다.
로지스틱 회귀는 구현하기 쉽고 이상치와 기타 데이터 문제에 상당히 탄력적이기 때문에 로지스틱 회귀를 사용하면 많은 머신러닝 문제를 잘 해결할 수 있으며, 다른 유형의 지도 학습보다 실용성과 성능이 뛰어나다.
[머신러닝] 로지스틱 회귀
이전 내용 [머신러닝] 회귀 - 규제 선형 모델: 릿지, 라쏘, 엘라스틱넷이전 내용 [머신러닝] 회귀 - 다항 회귀와 과대(과소) 적합이전 내용 [머신러닝] 회귀 - LinearRegression 클래스사이킷런 LinearReg
puppy-foot-it.tistory.com
로지스틱 회귀 수행하기
- 로지스틱 함수: 주어진 입력 변수에 대해 0과 1 사이의 출력 변수를 생성하는 S자형 곡선(시그모이드 곡선, sigmoid curve)이다. 출력 변수가 0과 1 사이이므로 확률을 표현할 때도 사용한다.
[하나의 입력 변수 x에 대한 확률 y를 출력하는 로지스틱 함수 공식]
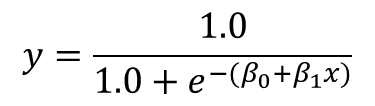
- x 변수: 독립 변수(입력 변수)
- 𝛽_0, 𝛽_1: 풀어야 할 계수 ( 𝛽_0: 절편, 𝛽_1:x에 대한 기울기)
로지스틱 회귀는 선형 회귀와 밀접한 관계가 있어 𝛽_0 과 𝛽_1은 선형 함수와 닮은 꼴로 지수에 들어가 있다.
𝛽_0 는 단순 선형 회귀의 b에, 𝛽_1은 단순 선형 회귀의 m에 해당하며, 지수에 있는 이 선형 함수를 로그 오즈(log-odds) 함수라고 하며, 전채 로지스틱 함수는 x값에 따라 바뀌는 확률을 출력하기 위한 S자형 곡선을 만든다.
[파이썬에서 로지스틱 함수 구현하기]
파이썬에서 로지스틱 함수를 구현하려면 math 패키지의 exp() 함수로 e를 표현한다.
# 파이썬에서 로지스틱 함수 구현하기
import math
def predict_probability(x, b0, b1):
p = 1.0 / (1.0 + math.exp(-(b0 + b1 * x)))
return p
b0 = -2.823, b1 = 0.62 라고 가정하고 심파이를 사용하여 그래프를 그려본다.
[심파이를 사용한 로지스틱 함수 그리기]
# 심파이를 사용해 로지스틱 함수 그리기
from sympy import *
b0, b1, x = symbols('b0 b1 x')
p = 1.0 / (1.0 + exp(-(b0 + b1 * x)))
p = p.subs(b0, -2.832)
p = p.subs(b1, 0.620)
print(p)
plot(p)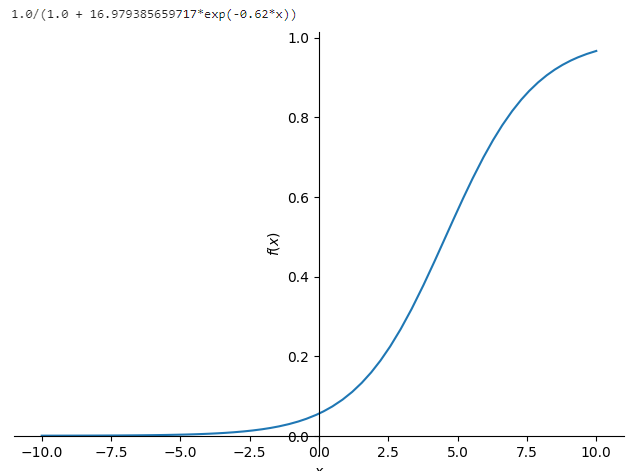
선형 회귀와 마찬가지로 로지스틱 회귀를 둘 이상의 입력 변수(x_1, x_2, ... , x_n)로 확장할 수 있고, 공식에 더 많은 𝛽_x 계수를 추가하면 된다.
로지스틱 회귀 훈련하기
주어진 훈련 데이터셋에서 로지스틱 회귀 모델을 훈련하려면 먼저 데이터에는 10진수, 정수, 이진 변수가 혼합될 수 있지만 출력 변수는 이진 (0또는 1) 이어야 한다.
또한, 입력과 출력 데이터에서 로지스틱 함수에 맞는 𝛽_0 과 𝛽_1 계수를 찾아야 한다. 이때에는 주어진 로지스틱 함수가 관측된 데이터를 출력할 가능성을 최대하화하는 최대 가능도 추정(MLE, maximum likelihood estimation)을 사용한다.
최대 가능도 추정을 계산하기 위해 경사 하강법을 사용하거나 계산을 대신하는 라이브러리를 사용할 수 있다.
◆ 사이킷런 사용하기
# 사이킷런으로 환자 데이터에 로지스틱 회귀 수헹
from sympy import *
import pandas as pd
from sklearn.linear_model import LogisticRegression
# 데이터 로드
df = pd.read_csv('http://bit.ly/33ebs2R', delimiter=',')
# (마지막 열 제외한 모든 열) 입력 변수로 추출
X = df.values[:, :-1]
# 마지막 열을 출력으로 추출
Y = df.values[:, -1]
# 패널티 없이 로지스틱 회귀 수행
model = LogisticRegression(penalty=None)
model.fit(X, Y)
# beta1 파라미터 출력
b1 =model.coef_.flatten()
print(b1)
# beta0 파라미터 출력
b0 = model.intercept_.flatten()
print(b0)
# 그래프 그리기
b0, b1, x = symbols('b0 b1 x')
p = 1.0 / (1.0 + exp(-(b0 + b1 * x)))
p = p.subs(b0, -3.175)
p = p.subs(b1, 0.692)
print(p)
plot(p)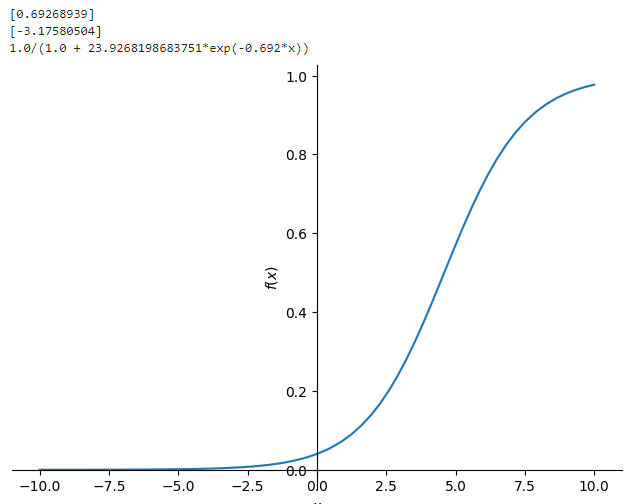
| - penalty 매개변수를 None으로 지정했는데, 이 매개변수에 l1 또는 l2와 같은 규제(regularization)를 지정할 수 있다. - 원소가 하나이나 다차원 행렬로 출력되기 때문에 계수와 절편에 flatten() 메서드 적용 ※ flatten (평탄화): 수치 행렬을 더 작은 차원으로 축소하는 것. (원소 개수보다 차원이 더 많은 경우 필요) |
◆ 최대 가능도와 경사 하강법 사용하기
최대 가능도 추정을 사용하면 로지스틱 회귀를 직접 구현할 수 있다.
최대 가능도 추정은 주어진 로지스틱 함수가 관측된 데이터를 출력할 가능성을 최대화하며 경사 하강법 또는 확률적 경사 하강법을 적용해 로지스틱 함수를 데이터 포인트에 가장 가깝게 만드는 𝛽_0 과 𝛽_1 을 찾는 것이다. 이 경우에는 주어진 로지스틱 회귀 함수에 대해 모든 데이터 포인트가 나타날 가능도를 계산한다.
[주어진 로지스틱 회귀에 대해 모든 포인트를 관측할 결합 확률 계산하기]
# 주어진 로지스틱 회귀에 대해 모든 포인트를 관측할 결합 확률 계산하기
import math
import pandas as pd
patient_data = pd.read_csv('http://bit.ly/33ebs2R', delimiter=',').itertuples()
b0 = -3.17576395
b1 = 0.69267212
def logistic_function(x):
p = 1.0 / (1.0 + math.exp(-(b0 + b1 * x)))
return p
# 결합 확률 계산
joint_likelihood = 1.0
for p in patient_data:
if p.y == 1.0:
joint_likelihood *= logistic_function(p.x)
elif p.y == 0.0:
joint_likelihood *= (1.0 - logistic_function(p.x))
print(joint_likelihood)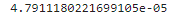
[if 표현식 없이 결합 확률 계산하기]
# if 표현식 없이 결합 확률 계산하기
import math
import pandas as pd
patient_data = pd.read_csv('http://bit.ly/33ebs2R', delimiter=',').itertuples()
b0 = -3.17576395
b1 = 0.69267212
def logistic_function(x):
p = 1.0 / (1.0 + math.exp(-(b0 + b1 * x)))
return p
# 결합 확률 계산
joint_likelihood = 1.0
for p in patient_data:
joint_likelihood *= logistic_function(p.x) ** p.y * (1.0 - logistic_function(p.x)) ** (1.0 - p.y)
print(joint_likelihood)
[로그 덧셈 사용]
# 로그 덧셈 사용
import math
import pandas as pd
patient_data = pd.read_csv('http://bit.ly/33ebs2R', delimiter=',').itertuples()
b0 = -3.17576395
b1 = 0.69267212
def logistic_function(x):
p = 1.0 / (1.0 + math.exp(-(b0 + b1 * x)))
return p
# 결합 확률 계산
joint_likelihood = 0.0
for p in patient_data:
joint_likelihood += math.log(logistic_function(p.x) ** p.y * (1.0 - logistic_function(p.x)) ** (1.0 - p.y))
joint_likelihood = math.exp(joint_likelihood)
print(joint_likelihood)
위의 식에서 𝛽_0 과 𝛽_1에 대한 편도함수를 심파이로 계산해본다.
[심파이로 로지스틱 회귀에 대한 결합 확률 표현하기]
# 심파이로 로지스틱 회귀에 대한 결합 확률 표현하기
from sympy import *
b, m, i, n = symbols('b m i n')
x, y = symbols('x y', cls=Function)
joint_likelihood = Sum(log((1.0 / 1.0 + exp(-(b + m * x(i)))) ** y(i)
* (1.0 - (1.0 / (1.0 + exp(-(b + m * x(i)))))) ** (1 - y(i))),
(i, 0, n))
lambdify() 함수를 적용해 경사 하강법에 사용
[로지스틱 회귀에 경사 하강법 사용하기]
# 로지스틱 회귀에 경사 하강법 사용하기
from sympy import *
import pandas as pd
# 데이터 포인트 로드
points = list(pd.read_csv('https://tinyurl.com/y2cocoo7').itertuples())
# 기호 정의
b0, b1 = symbols('b0 b1')
i, n = symbols('i n')
x, y = symbols('x y', cls=Function)
# 로지스틱 회귀 가능도 함수 정의
joint_likelihood = Sum(log(1 / (1 + exp(-(b0 + b1 * x(i)))) ** y(i) * (1 - (1 / (1 + exp(-(b0 + b1 * x(i)))))) ** (1 - y(i))), (i, 0, n))
# b1에 대한 편도함수 계산
d_b1 = diff(joint_likelihood, b1).subs(n, len(points) - 1).doit().replace(x, lambda i: points[i].x).replace(y, lambda i: points[i].y)
# b0에 대한 편도함수 계산
d_b0 = diff(joint_likelihood, b0).subs(n, len(points) - 1).doit().replace(x, lambda i: points[i].x).replace(y, lambda i: points[i].y)
# 빠른 계산을 위해 lambdity() 함수로 변환
d_b1 = lambdify([b1, b0], d_b1)
d_b0 = lambdify([b1, b0], d_b0)
# 경사 하강법 수행
b1 = 0.01
b0 = 0.01
L = .01
for j in range(10000):
b1 += d_b1(b1, b0) * L
b0 += d_b0(b1, b0) * L
print(b1, b0)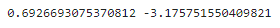
- 𝛽_0 과 𝛽_1 에 대한 편도함수를 계산한 후 데이터 포인트의 개수 n과 x, y 값을 대입한다.
- 효율성을 위해 lambdify() 함수를 사용해 편도함수를 파이썬 함수로 변환한다.
- 경사 하강법 수행. (최소화가 아닌 최대화를 시도하기 때문에 𝛽_0 과 𝛽_1 을 더한다)
★ 예측 만들기
LogisticRegression()을 포함해 사이킷런의 다른 모델 객체에서도 predict() 와 predict_prob() 함수를 사용해 예측을 만들 수 있다.
- predict(): 특정 클래스 예측(참 도는 거짓)
- predict_prob(): 각 클래스에 대한 확률 출력
다음 내용
[개발자를 위한 수학] 로지스틱 회귀와 분류 - 2
이전 내용 [개발자를 위한 수학] 로지스틱 회귀와 분류 - 1로지스틱 회귀(logistic regression) 하나 이상의 독립 변수가 주어졌을 때 결과의 확률을 예측하는 알고리즘. 로지스틱은 선형 회귀와 유사
puppy-foot-it.tistory.com
[출처]
개발자를 위한 필수 수학
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [개발자를 위한 수학] 신경망 - 1 (3) | 2024.10.20 |
|---|---|
| [개발자를 위한 수학] 로지스틱 회귀와 분류 - 2 (0) | 2024.10.18 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.9)-2 (6) | 2024.10.18 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.9)-1 (2) | 2024.10.17 |
| [개발자를 위한 수학] 선형 회귀 - 3 (7) | 2024.10.17 |



