신경망(neural network)
신경망은 입력 변수와 출력 변수 사이에 가중치, 편향, 비선형 함수로 이루어진 층을 쌓아 구성한다.
딥러닝(Deep learning)은 신경망의 한 종류이며, 가중치와 편향을 가진 노드(node)로 구성된 여러 개의 은닉층(hidden layer)을 사용한다. 각 노드는 비선형 함수(또는 활성화 함수)를 통과하기 전에는 선형 함수와 유사한데, 확률적 경사 하강법과 같은 최적화 기법을 사용해 잔차를 최소화하는 최적의 가중치와 편향을 찾는다.
신경망에서는 입력을 입력층 (input layer), 출력을 계산하기 위한 마지막 층을 출력층(output layer), 그 사이에 놓은 층을 은닉층이라 부른다.
언제 신경망과 딥러닝을 사용하는가
신경망과 딥러닝은 분류와 회귀에 사용할 수 있고, 신경망에는 여러 종류가 있다.
- 합성곱 신경망: 이미지 인식에 자주 사용
- LTSM 신경망: 시계열 예측에 사용
- 순환 신경망(RNN): 텍스트-투-스피치 애플리케이션에 자주 사용
[같이 보면 좋은 글들]
[딥러닝] Deep Learning 기본 개념 및 문제
딥러닝의 정의출처: 내 삶속 AI: 알게모르게 스며든 AI 기술, 제대로 알고쓰자! 딥러닝은 인공 지능(AI) 연구 분야의 하나로, 인간의 뇌가 정보를 처리하고 학습하는 방식을 모방한 인공 신경망
puppy-foot-it.tistory.com
[신경망 모델] 트랜스포머(Transformer) 모델이란?
트랜스포머 모델이란? 트랜스포머 모델(Transformer)은 문장 속 단어와 같은 순차 데이터 내의 관계를 추적해 맥락과 의미를 학습하는 신경망이다. 자연어 처리(NLP)와 딥러닝 분야에서 혁신적인
puppy-foot-it.tistory.com
[CNN 구조] 합성곱 신경망을 사용한 컴퓨터 비전
CNN 구조 전형적인 CNN 구조는 합성곱 층을 몇 개 쌓고(각각 ReLU 층을 그 뒤에 놓고), 그 다음에 풀링 층을 쌓고, 그 다음에 또 합성곱 층을 몇 개 더 쌓고, 그 다음에 다시 풀링 층을 쌓는 식이다.네
puppy-foot-it.tistory.com
간단한 신경망 모델 예제
어떤 색상의 배경에서 글꼴이 밝아야 하는지(1) 아니면 어두워야 하는지(0)를 예측하는 모델.
각 값은 컴퓨터 과학에서 색상을 표현하는 RGB 값(0에서 255 사이)을 입력 변수로 특정 함수를 훈련해 밝은 글꼴을 사용할지, 어두운 글꼴을 사용할지 출력한다.
이 예측의 출력은 확률로 표현되며, RGB를 색상값으로 바꿔 신경망의 출력이 0.5 이상이면 밝은 글꼴을, 0.5 미만이면 어두운 글꼴을 제안한다.
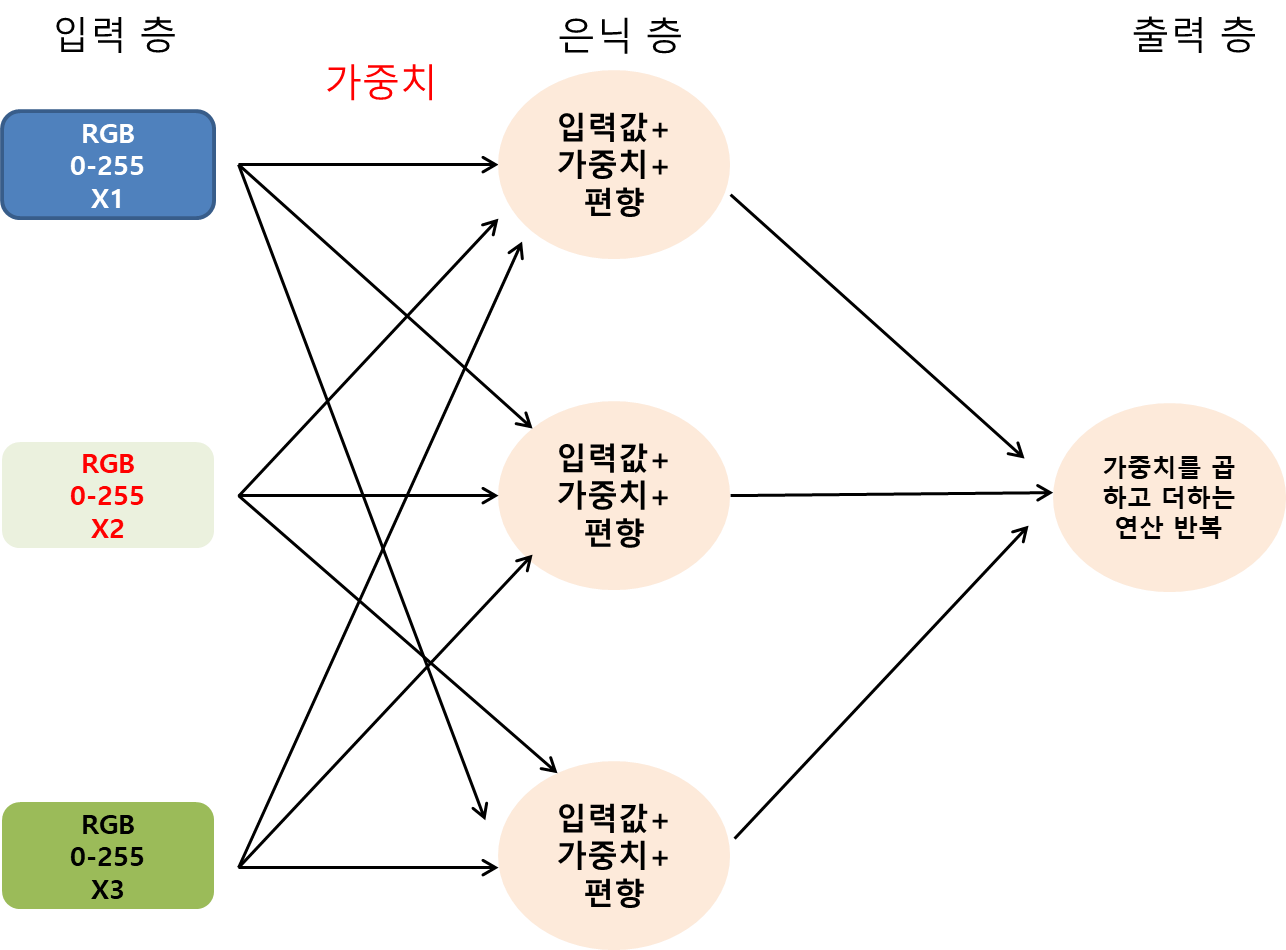
- 왼쪽의 첫 번째 층은 단순히 세 변수의 입력 (RGB의 색상값)
- 은닉(가운데) 층에는 입력과 출력 사이에 가중치와 편향의 함수인 노드 세 개가 있음.
- 각 노드는 가중치 W와 편향 B을 가진 선형 함수이고 입력 변수 X와 곱한 후 더한다.
- 은닉 노드와 출력 노드 사이에는 또 다른 가중치가 있고, 은닉 노드와 출력 노드에는 모두 편향이 있다.
- 출력 노드에서는 은닉 층에서 가중치를 곱하고 더하여 얻은 결과를 가져와서 입력하면 다른 가중치와 편향이 적용된다.
- 가중치와 편향을 찾기 위해 역전파라는 추가 도구 필요.
◆ 활성화 함수
활성화 함수: 노드에서 가중치를 곱해 더한 값을 볗놘하거나 압축하는 비선형 함수. 신경망이 데이터를 효과적으로 분리해 분류 작업을 수행할 수 있도록 돕는다.
활성화 함수가 없다면 은닉 층의 성능이 떨어지고 하나의 선형 회귀보다 좋지 않다.
- 렐루(ReLU) 활성화 함수: 은닉 노드에서 출력된 음숫값을 모두 0으로 만든다. 즉, 가중치와 입력을 곱하고 편향을 더한 값이 음수가 되면 렐루 함수가 0으로 바뀐다. (만약 양수이면 양수 그대로 출력)
훈련 속도와 그레이디언트 소실 문제를 완화하기 때문에 신경망과 딥러닝의 은닉 층에 널리 사용.
※ ReLU(rectified linear unit)
※ 그레이디언트 소실: 편도함수 기울기가 작아지면서 너무 일찍 0에 가까워져 학습이 중지되는 현상
[심파이를 사용한 렐루 함수 그리기]
# 렐루 함수
from sympy import *
x = symbols('x')
relu = Max(0, x)
plot(relu)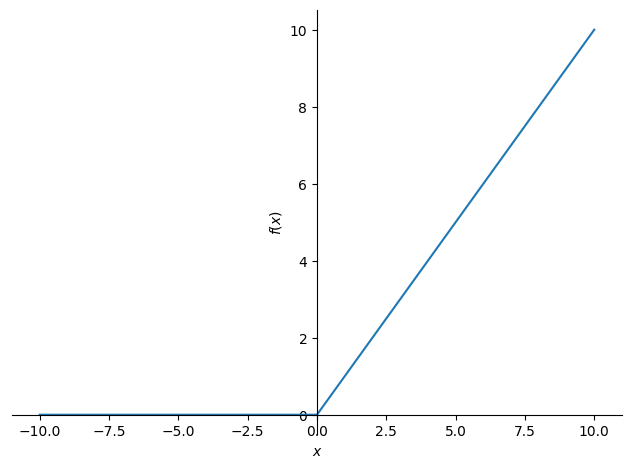
출력 층은 은닉 층의 계산 결과를 가져와 분류 예측처럼 해석 가능한 결과로 변환하는 중요한 역할이며, 은닉 층에서 들어오는 각 값에 가중치를 부여한 다음 편향을 더한다. 그다음 이 결괏값을 로지스틱 함수에 전달해 0과 1 사이의 수치를 출력한다.
[심파이의 로지스틱 활성화 함수]
# 심파이의 로지스틱 활성화 함수
from sympy import *
x = symbols('x')
logistic = 1 / (1 + exp(-x))
plot(logistic)
- 활성화 출력: 가중치를 곱하고 편향을 더한 노드의 출력이 활성화 함수를 통과하면 활성화 함수를 통해 필터링되는 것
은닉 층에서 활성화 출력이 만들어지면 다음 층으로 신호가 전달될 준비가 된 것이다. 활성화 함수는 신호를 강화하거나 약화하거나 그대로 둘 수 있다.
<일반적인 활성화 함수>
| 이름 | 사용하는 일반적인 층 |
설명 | 참고 |
| 선형(linear) | 출력 층 | 값을 그대로 둠 | 자주 사용하지 않음 |
| 로지스틱 | 출력 층 | S자형 시그모이드 곡선 | 0과 1 사이로 값을 압축하며, 이진 분류에 주로 사용 |
| 하이퍼볼릭 탄젠트 (hyperbolic tangent) |
은닉 층 | tahn, -1에서 1 사이의 S자형 시그모이드 곡선 | 평균을 0에 가깝게 만들어 데이터를 중앙에 맞춤 |
| 렐루(ReLU) | 은닉 층 | 음숫값을 0으로 만듦 | 시그모이드나 tahn 보다 빠른 활성화 함수로 그레이디언트 소실 문제를 완화하고 계산 비용이 저렴해 널리 사용 |
| 리키 렐루(Leaky ReLU) | 은닉 층 | 음숫값에 0.01을 곱함 | 음숫값을 제거하지 않고 줄이는 렐루의 변형 |
| 소프트맥스 | 출력 층 | 모든 출력 노드를 더해 1.0이 되도록 만듦. | 다중 분류에 유용하고 출력의 크기를 조정해 합을 1.0으로 만듦. |
※ 회귀 문제일 경우 임의의 실수를 예측하므로 출력 층에 비선형 함수를 사용하지 않고 선형 활성화 함수 사용
이 신경망은 겉보기에는 두 가지 클래스를 구분하는 것처럼 보이나, 실제로는 하나의 클래스를 모델링한다 (글꼴이 밝은지 아니면 아닌지를 구분). 여러 클래스를 지원하려면 각 클래스에 대한 출력 노드를 추가하면 되는데, 만약 0에서 9까지를 인식하려면 출력 노드가 10개 있어야 하며, 여러 클래스가 있는 경우 소프트맥스를 출력 활성화로 사용한다.
◆ 정방향 계산
[피드 포워드 신경망을 생성하는 파이썬 코드]
※ 피드 포워드: 신경망에 각 픽셀의 값을 입력한 후 각 층의 결과를 신경망의 앞쪽으로 계속 전달해 출력 결과를 얻는 것.
# 피드 포워드 신경망 생성
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
all_data = pd.read_csv('http://tinyurl.com/y2qmhfsr')
# 입력값을 추출해 255로 나눔
all_inputs = (all_data.iloc[:, 0:3].values / 255.0)
all_outputs = all_data.iloc[:, -1].values
# 훈련 데이터와 테스트 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(all_inputs, all_outputs, test_size=1/3)
n = X_train.shape[0] # 훈련 샘플 개수
# 신경망의 가중치와 편향을 랜덤하게 초기화 (w: 가중치, b: 편향)
w_hidden = np.random.rand(3, 3)
w_output = np.random.rand(1, 3)
b_hidden = np.random.rand(3, 1)
b_output = np.random.rand(1, 1)
# 활성화 함수
relu = lambda x: np.maximum(x, 0)
logistic = lambda x: 1 / (1 + np.exp(-x))
# 입력을 신경망에 통과시키고 출력 얻음
def forward_prop(X):
Z1 = w_hidden @ X + b_hidden
A1 = relu(Z1)
Z2 = w_output @ A1 + b_output
A2 = logistic(Z2)
return Z1, A1, Z2, A2
# 정확도 계산
test_predictions = forward_prop(X_test.transpose())[3] # 출력 층의 결과 A2 만 사용
test_comparisons = np.equal((test_predictions >= .5).flatten().astype(int), y_test)
accuracy = sum(test_comparisons.astype(int) / X_test.shape[0])
print("정확도: {:.2f}".format(accuracy))

- RGB 입력값과 출력값(밝음 1, 어두움 0) 이 포함된 데이터셋 (CSV 파일)
- 입력 열 R, G, B 의 값을 1/255 로 나누어 0과 1 사이로 만듦. (숫자 공간이 압축되어 훈련에 도움)
- 사이킷런을 사용해 데이터 분할 (2/3 훈련용, 1/3 테스트용)
[코드 해석 하기: 넘파이로 만든 가중치 행렬과 편향 벡터]
w_hidden = np.random.rand(3, 3)
w_output = np.random.rand(1, 3)
b_hidden = np.random.rand(3, 1)
b_output = np.random.rand(1, 1)(상단) 코드 중의 일부인 위 부분은 신경망의 은닉 층과 출력 층의 가중치와 편향을 선언한다.
가중치와 편향은 0과 1 사이의 임의의 값으로 초기화된다.
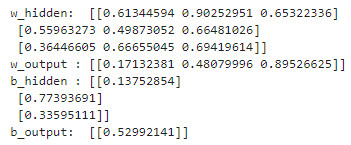
w_hidden 은 은닉 층의 가중치이며,
첫 번째 행은 첫 번째 노드의 가중치 W_1, W_2, W_3을 나타냄.
두 번째 행은 두 번째 노드의 가중치 W_4, W_5, W_6을 나타냄.
세 번째 행은 세 번째 노드의 가중치 W_7, W_8, W_9를 나타냄.
출력 층(w_output)에는 노드가 하나만 있으므로 행렬에 W_10, W_11, W_12 가중치로 이루어진 행 하나만 있음.
b_hidden 은 은닉 층에 대한 편향이며 행이 3개,
b_output 은 출력 층에 대한 편향이며 행이 1개.
▶ 노드가 하나면 행도 하나이며, 행의 각 열에는 해당 노드의 가중치 값이 있고, 노드 당 편향 역시 하나이다.
[코드 해석 하기: 신경망의 활성화 함수와 정방향 계산 함수]
# 활성화 함수
relu = lambda x: np.maximum(x, 0)
logistic = lambda x: 1 / (1 + np.exp(-x))
# 입력을 신경망에 통과시키고 출력 얻음
def forward_prop(X):
Z1 = w_hidden @ X + b_hidden
A1 = relu(Z1)
Z2 = w_output @ A1 + b_output
A2 = logistic(Z2)
return Z1, A1, Z2, A2이 코드는 행렬 곱셈과 행렬-벡터 곱셈을 사용해 가중치, 편향, 활성화 함수를 통해 세 개의 RGB 입력값에 대한 계산을 수행해 전체 신경망을 간결하게 실행하기 때문에 중요하다.
- 주어진 입력값을 받아 출력값을 반환하는 relu() 와 logistic() 활성화 함수 선언
- forward_prop() 함수: R, G, B 값이 포함된 입력 X에 대해 전체 신경망 실행하며 네 개의 행렬(A1, Z1, A2, Z2) 반환
- 1과 2는 각각 첫 번째 층과 두 번재 층에 속하는 연산을 나타냄.
- Z는 활성화 함수를 거치기 전의 출력을 나타냄
- A는 활성화 함수를 통과한 출력을 나타냄
- A1, Z1: 은닉 층의 출력. (Z1: X에 가중치와 편향을 적용한 결과. A1: Z1을 렐루 활성화 함수에 통과시켜 얻은 값)
- Z2: A1에 출력 층의 가중치와 편향을 적용한 결과
- A2: Z2 출력이 다시 활성화 함수인 로지스틱 함수를 통과한 값. 출력 층의 예측 확률로 0과 1 사이의 값을 가짐 (두 번째 층의 활성화된 출력)
Z_1 = w_hidden * X + b_hidden
A_1 = ReLU(Z_1)
Z_2 = w_output * A_1 + b_output
A_2 = logistic(Z_2)
[코드 해석 하기: 정확도 계산]
test_predictions = forward_prop(X_test.transpose())[3] # 출력 층의 결과 A2 만 사용
test_comparisons = np.equal((test_predictions >= .5).flatten().astype(int), y_test)
accuracy = sum(test_comparisons.astype(int) / X_test.shape[0])
print("정확도: {:.2f}".format(accuracy))가중치와 편향은 무작위로 생성되므로 답변이 달라질 수 있다.
파라미터가 무작위로 생성되었기 때문에 정확도가 높아 보일 수 있지만, 출력 예측은 밝음 또는 어두움 두 가지라는 점도 기억해야 한다. 즉, 이 코드를 실행함으로써 얻은 약 67%의 정확도는 높은 수치가 아니다.
다음 내용
[개발자를 위한 수학] 신경망 - 2
이전 내용 [개발자를 위한 수학] 신경망 - 1신경망(neural network) 신경망은 입력 변수와 출력 변수 사이에 가중치, 편향, 비선형 함수로 이루어진 층을 쌓아 구성한다.딥러닝(Deep learning)은 신경망
puppy-foot-it.tistory.com
[출처]
개발자를 위한 필수 수학
'[파이썬 Projects] > <파이썬 - 수학 | 통계학>' 카테고리의 다른 글
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.10) (1) | 2024.10.20 |
|---|---|
| [개발자를 위한 수학] 신경망 - 2 (5) | 2024.10.20 |
| [개발자를 위한 수학] 로지스틱 회귀와 분류 - 2 (0) | 2024.10.18 |
| [개발자를 위한 수학] 로지스틱 회귀와 분류 - 1 (3) | 2024.10.18 |
| [파이썬+통계학] 현대통계학 연습문제 파이썬 구현(ch.9)-2 (6) | 2024.10.18 |



